This lesson investigates sequences that are defined recursively by examining the graph of the sequence and looking at the associated table of values.

Defining a Recursive Sequence

A recursive sequence defines a term a_n using one or more of the previous terms of the sequence. Because each term is defined using previous terms, the first few terms of the sequence must be defined explicitly.

Explore the recursive sequence shown below that defines each term of the sequence as twice the previous term, a_n = 2a_{n - 1}. The first term of the sequence is defined to be 1. The sequence may be written symbolically as two statements.

a₁ = 1

a_n = 2a_{n - 1}, for n = 2, 3, 4, 5,...

Graphing the Recursive Sequence

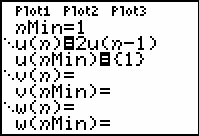
Define the sequence in the Y= Editor.

• Set u1(n) = 2 · u(n-1). Press to enter u.

The function notation u(n - 1) represents the function value at n - 1 and also represents the (n - 1)^st term of the sequence. There is no multiplication sign between u and (n - 1) because it is given in function notation.

The first term of the sequence must also be entered so that the calculator will have a value with which to evaluate the second term. Subsequent terms will be determined by using previously computed terms.

• Set nMin = 1.
• Set u(nMin) = 1.

u(nMin) represents u(1), the first term of the sequence.


• Set the window parameters to the values below.

nMin = 1	Xmin = -1	Ymin = -1
nMax = 10	Xmax = 10	Ymax = 100
PlotStart = 1	Xscl = 1	Yscl = 10
PlotStep = 1

• Display the graph of the sequence

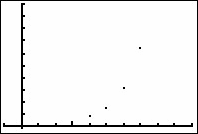
The graph suggests that the sequence gets large without bound as n approaches infinity. If this is so, then the sequence diverges.

Creating a Table of Values

The divergence of the sequence can by supported by viewing a table of values.

• Set TblStart = 1 and Tbl = 1 in the Table Setup dialog box.
• Set Indpnt to "Auto."
• Display the Table.

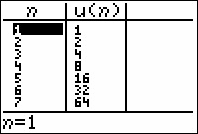
It appears from the table that this sequence is the sequence a_n = 2^{n - 1}. The sequence a_n = 2^{n - 1} is an example of a geometric sequence. This particular geometric sequence is in fact divergent.

Defining a Recursive Sequence Requiring Two Previous Values

In the sequence investigated above, each term was defined as twice the value of the preceding term. Recursive sequences can also be defined using more than one preceding term.

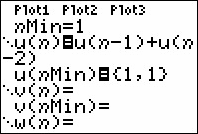
Explore the recursive sequence that defines each term as the sum of the two previous terms where a₁ = a₂ = 1 and a_n = a_n-1 + a_n-2 for n = 3, 4, 5,... .

• Return to the Y= editor.
• Set nMin = 1.
• Set u(n)=u(n-1)+u(n-2).
• Set u(nMin) = {1,1}.

The initial value u(nMin) is the list {1,1}, which represents the values of the first two terms. The symbols '{' and '}' are found above the parentheses keys.

• Set TblStart = 1 and Tbl = 1.

23.3.1 Display the table and, if possible, identify the sequence shown.
Click here for the answer.

Although sequences can be defined recursively using more than the previous two terms, the TI-83 is not able to do that.