This lesson explores series and partial sums of infinite series. Series are used in many applications including integration, approximation, and the solution of differential equations. These applications arise in many disciplines, especially physics and chemistry.

Defining a Series

A series, which is not a list of terms like a sequence, is the sum of the terms in a sequence. If the series has a finite number of terms, it is a simple matter to find the sum of the series by adding the terms. However, when the series has an infinite number of terms the summation is more complicated and the series may or may not have a finite sum.

Defining Partial Sums

A partial sum of an infinite series is the sum of a finite number of consecutive terms beginning with the first term. When working with infinite series, it is often helpful to examine the behavior of the partial sums.

Suppose an infinite sequence is defined by . The terms of the sequence are

.

The first four partial sums of the associated infinite series are computed below, where s_k represents the sum of the first k terms of the sequence.

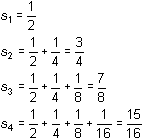
Each of the results shown above is a partial sum of the series which is associated with the sequence .

Defining the Sequence of Partial Sums of a Series

The partial sums of a series form a new sequence, which is denoted as {s₁, s₂, s₃, s₄,...}. For the series given above, the sequence of partial sums is .

If the sequence of partial sums for an infinite series converges to a limit L, then the sum of the series is said to be L and the series is convergent. Otherwise, the infinite series does not have a sum and it is divergent.

Finding Partial Sums of Series

The TI-83's sum( function and the Sequence Graphing mode are useful tools in understanding the sequence of partial sums of series.

Using the sum( Function

Partial sums can be computed with the sum function and may be used to help explore whether or not an infinite series converges. If it is convergent, the partial sums can also help estimate the sum of the series.

The sum( Function The sum( function returns the sum of the terms of any list. The syntax is sum(list). If the seq( command is being used to generate the list, then the sum of the list can be found with the following syntax sum(seq (expression, var, min, max, step))

Investigate whether converges.

• Open the LIST MATH menu by pressing [LIST] .
  "5: sum(" is the fifth item in this menu.

• Select "5:sum(" to paste the "sum(" command to the Home screen.

Beginning with Zero

Explore the partial sums of the series . The first term in this series corresponds to
k = 0, and that term is the first partial sum as well. The second partial sum is found by adding the first two terms, corresponding to k = 0 and k = 1. In general, the nth partial sum is found by adding the terms corresponding to k = 0, 1, ..., (n - 1).

• Complete the command sum(seq((2^K + 5)/3^K, K , 0 , 4)).

  Recall seq( is in the LIST OPS menu.

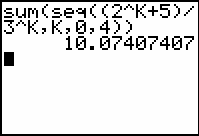
This result is called the fifth partial sum because the first five terms corresponding to k = 0, 1, 2, 3, 4 were added.

23.2.1 Approximate the tenth partial sum of the infinite series .
Click here for the answer.

Graphing the Sequence of Partial Sums

The graph of the sequence of partial sums for the infinite series can be created by defining the sequence of partial sums in the Y= Editor in Sequence Graph mode.

• Define u(n) = sum(seq((2^K+5)/3^K, K, 0, n)) in the Y= Editor.

Recall that n is the independent variable in Sequence Graphing mode and it can be entered using the key.

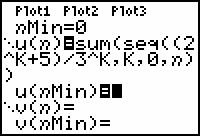
• Use the following window values:

nMin = 0	Xmin = -1	Ymin = -1
nMax = 10	Xmax = 11	Ymax = 15
PlotStart = 1	Xscl = 1	Yscl = 1
PlotStep = 1

• Graph the sequence of partial sums by pressing

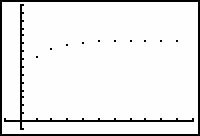
Each point of this graph represents a partial sum.

• Trace to the tenth partial sum (n = 9).

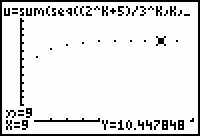
This should be the same value for the tenth partial sum that you computed earlier on the Home Screen.

23.2.2 The graph of the sequence of partial sums appears to level off. What does this suggest?
Click here for the answer.

Creating a Table of Values for the Partial Sums

Make a table to show the partial sums.

• Open the Table Setup dialog box by pressing [TBLSET].
• Set TblStart = 0 and Tbl = 1.
• Open the table by pressing [TABLE]

The Ask Mode

You can compute partial sums of your choosing by returning to the Table Setup dialog box and selecting the Ask mode.

• Open the Table Setup dialog box by pressing [TBLSET].
• On the line labeled "Indpnt" highlight "Ask."

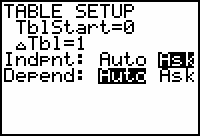
• Return to the table by pressing [TABLE].
• Enter 9 for n in the first row and press .
• Move the cursor to the next row and enter 15 for n.
• Move the cursor to the next row and enter 25 for n.
• Move the cursor to the next row and enter 50 for n.

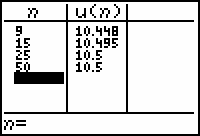
The table provides further evidence that the series converges.

It is impossible to determine for certain whether or not a series converges and/or to determine the sum of a series by exploring partial sums. Many divergent infinite series may appear to converge and have a sum when studied using the methods discussed so far in this lesson.

Tests for Convergence

Both the graph and table for the series of partial sums give some evidence a series converges. However, analytic methods must be used to be certain that a series converges. You should consult a calculus text for descriptions of tests for convergence and divergence for infinite series.

23.2.3 The ratio test is an analytic test for convergence and it shows that the series being discussed, , converges. To what value do you think the series converges?
Click here for the answer.