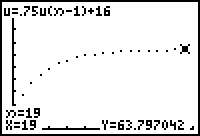Module 23 - Answers
 
Lesson 1
 
 Answer 1
 
23.1.1  

As n gets large the terms in the sequence get closer to zero.

 
 Answer 2
 
23.1.2  

The last several values appear to level off on the x-axis suggesting that 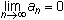. This is graphical evidence the sequence converges to zero.

 
 Answer 3
 
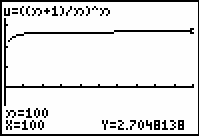
23.1.3   The sequence appears to converge to approximately 2.7.

 
Lesson 2
 
 Answer 1
 
23.2.1 s10 10.4478
 
 Answer 2
 
23.2.2   The fact that the sequence of partial sums appears to level off suggests that the sequence of partial sums converges, which means the infinite series converges. Trying larger values for nMax may add more evidence for this conclusion, but it is impossible to be certain that an infinite series converges based on a graph or a table.
 
 Answer 3
 
23.2.3  

The graph and table of partial sums indicate that the series converges to approximately 10.5.

 
 Answer 4
 
21.2.4   In the previous table the 26th and 51st partial sums were both approximately 10.5. So a reasonable estimate for the sum of the infinite series is 10.5.
 
Lesson 3
 
 Answer 1
 
23.3.1

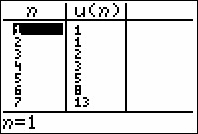
This is the Fibonacci sequence.

 
Self Test
 
 Answer 1
 
1, 1, 0.5, 0.1667, 0.04167, 0.008333, 0.001389, 0.0001984, 0.00002480, 0.000002756
 
 Answer 2
 
2.71828
 
 Answer 3
 

The sequence appears to converge to approximately 0.377. The actual value is .

 
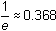 Answer 4
 
0.3751; 0.3715; 0.3697
 
 Answer 5
 

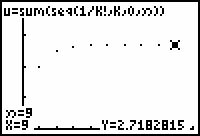
The series appears to converge to approximately 2.71828. The exact value is e.

 
 Answer 6
 

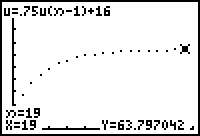
The sequence appears to converge to approximately 63.8. The exact value is 64.

 
 
  ©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy