Motion along a line was modeled in Lesson 15.1 with a polynomial function and Lesson 15.2 modeled harmonic motion along a line with a trigonometric function. In this lesson motion in a plane will be investigated.

The Problem

A baseball is hit at an angle of 20° above the horizon with an initial velocity of 152 ft/sec and from an initial height of 3 feet off the ground. Will the ball clear a 10-foot wall at a distance of 415 feet away from home plate?

Modeling the Motion

Because the ball's position is restricted to a plane that is vertical with respect to the ground, its motion can be modeled in two dimensions, where x represents the horizontal distance of the ball from home plate and y represents the height of the ball above the ground. The horizontal and vertical positions can each be written as a function of time.

The movement of the baseball in the plane can be modeled using the parametric equations below, where

1. v represents the ball's initial velocity,
2. h represents the ball's initial height,
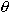3. represents the angle at which the ball is hit, and
4. t represents time in seconds since the ball was struck.

x(t) = v · t · cos

y(t) = -16t² + v · t · sin + h

In the given problem v = 152 ft/sec, h = 3 ft, and = 20°. Define the parametric equations so that the graph of the ball's path may be drawn.

• Set X_1T = 152 cos(20) T.
• Set Y_1T = -16T^2 + 152 sin(20) T + 3.

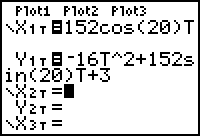
• Select Degree for the Angle mode in the Mode settings and Sequential for the Graph order mode.

• Some experimentation might be required to find a good window. Set the Viewing Window values to [0, 5, 0.1] x [0, 450, 50] x [-10, 50, 10].

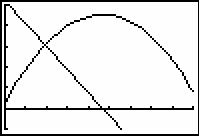
15.3.1 Graph the equations and use the Trace feature to decide if the ball clears the 10-foot fence that is 415 feet from where it was hit. Click here for the answer.

Finding Maximum Height

The path of the ball is an inverted parabola, so the maximum height occurs at the vertex, or local maximum.

To determine the maximum height of the ball:

1. Find the time when the derivative of the height (Y_1T) is equal to zero.
2. Evaluate the height function with that value of t.

• Set X_2T = X_1T.
• Set Y_2T = nDeriv(Y_1T,T,T).

• Graph the path and the derivative.

• Use the Solver in the Math menu to find when the derivative is zero. Press and scroll down to "0:Solver...".

• Press followed by the up arrow (if necessary) to enter the equation 0=Y_2T as shown below.

• Press and move the cursor to the equation T= (you may have a different number here). Then press [SOLVE] to solve for T.

 

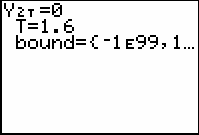
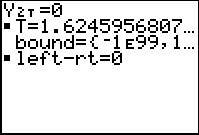
The ball reaches its maximum height at approximately t = 1.62 seconds.

There is No Zero Feature in Parametric Mode There is no Zero feature in the CALCULATE menu when the TI-83 is in Parametric mode. The zero can be approximated using the Solver feature.

15.3.2 Find the maximum height of the ball by evaluating Y_1T at the value of t = 1.62. Click here for the answer.

15.3.3 Use the second derivative test to justify that the value found in Question 15.3.2 corresponds to a local maximum. Click here for the answer.