In the previous lesson you found tolerances graphically. In this lesson you will use algebra to find the tolerances symbolically. This will prepare you to generalize the tolerances and develop the definition of limit.
Tolerances
The first tolerance you found in lesson 6.1 was in response to the question:
-
How close should x be to 3 so that
is within 0.1 of 2?
The x-Tolerance
The procedure to find the solution to the question above can be expressed using two compound inequalities.
-
Find a positive number
so that
whenever
Solving the Inequality
When the y-tolerance is 0.1 the x-tolerance can be found by solving the
compound inequality,
A compound (or extended) inequality is an inequality that compares more than two quantities and contains more than one inequality symbol.
, as shown below.
The sense of the compound inequality above was retained when each expression was squared because each expression represented a positive number.
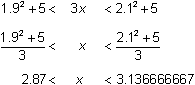
The solution of the compound inequality is approximately 2.87 < x < 3.136666667.
Notice that the solutions are the same as those found in Lesson 6.1 when you used the Intersect feature on the Graph screen.
Finding
Compare the inequalities below.
It follows that
and
.
Solving the two equations for
yields two different values:
and
. As in Lesson 6.1, the smaller of the two values is the correct answer:
.
A Smaller y-Tolerance
The second x-tolerance you found in Lesson 6.1 came from answering the question
-
How close should x be to 3 to ensure that
is within 0.01 of 2?
6.2.1 Restate the question above using compound inequalities. Click here for the answer.
6.2.2 Solve the first compound inequality in the answer to 6.2.1. Click here for the answer.
6.2.3 Compare the answer in 6.2.2 with the inequality 3 -
< x < 3 +
. Find a value of
, the x-tolerance. Click here for the answer.
Finding a Generalized Solution
Suppose that you are asked to find values of
that correspond to smaller and smaller y-tolerances around y = 2. Rather than going through the same process repeatedly for various y-tolerances, you could solve the problem once with a generalized y-tolerance.
Let the general y-tolerance be represented by
, the Greek letter "epsilon." The Greek letters delta,
, and epsilon,
, are used to represent small positive numbers.
The tolerance question then becomes
How close should x be to 3 so that
is within
of 2?
Finding the Generalized x-Tolerance
The procedure used to find the solution to the generalized tolerance question is
Given a positive number
, find a positive number
, so that
whenever
Solving the Generalized Inequality
The compound inequality
is solved below. The method of solution assumes that
is less than 2. If
is greater than 2, we can choose
= 1.
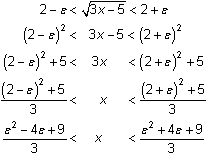
The solution to the generalized compound inequality is
Comparing the last inequality with
yields two equations:
and
The solutions to these equations are
and
If
is a small positive number
will be positive.
The smaller of these two values is
, which is the general solution.
Given any small positive value for
the last equation can be used to find the corresponding value for
. For example, when
= 0.01, this equation gives
= 0.0133, the same value found earlier.
Limits
When the values of the output can be made as close as we like to 2 by taking input values sufficiently close to 3, we say
-
The limit of the function
as x approaches 3 is equal to 2.
That is, the value of
gets closer to 2 as x gets closer to 3. The notation used to indicate this is
The limit is read "the limit of
as x approaches 3 is 2."
In the previous example we found that
guarantees that
whenever
Because for any positive
a corresponding positive
can be found that meets the conditions above,
This leads to the formal definition of a limit.
Definition of Limit
The value of the function when x = a is not relevant when finding a limit. Only the values of the function are considered as x approaches a.
Formally,
if for any
, there exists a
such that
whenever
Conceptually, f(x) approaches L as x approaches a, which can also be written
The value of the function when x = a is not relevant when finding a limit. Only the values of the function as x approaches a are considered.
6.2.4 Write a statement with compound inequalities that represents the conditions associated with
. Click here for the answer.