In this lesson you will define a function symbolically in the Y= editor and investigate the function on the Home screen.
Defining a Function
The function you will define is f(x) = 2x2 - 5x - 3.
-
Press
 , the first graphing key, to open the Y= editor.
, the first graphing key, to open the Y= editor.
-
Enter the function f(x) = 2x2 - 5x - 3 in Y1 by pressing





 .
.
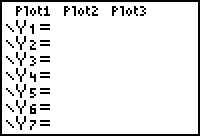
|
|||
|
|
|||

Evaluating a Function
Now that you have successfully defined the function f(x) = 2x2 - 5x - 3 in Y1, you can evaluate the function at x = 2 by evaluating the expression Y1(2) on the Home screen.
-
Return to and clear the Home screen by pressing
 [QUIT]
[QUIT]
 .
.
-
Open the Variables menu by pressing
 and then select the Y-Variables submenu by pressing
and then select the Y-Variables submenu by pressing
 .
.
-
Select the Function submenu by pressing
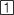 .
.
-
Paste the variable Y1 to the Home screen by pressing
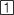 .
.
-
Finish the expression by pressing
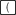
.gif) .
.
-
Evaluate the expression by pressing
 .
.

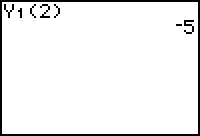
Editing the Last Entry
If you want to evaluate the function at x = 3 next, you can recall and edit the last expression on the Home screen rather than entering in the entire expression.
-
Press
 [Entry] to recall the last expression.
[Entry] to recall the last expression.
-
Move the cursor to the 2 by pressing
 twice.
twice.
-
Overwrite the 2 with a 3 by pressing
 .
.
-
Display the result by pressing
 .
.

Finding Zeros of Functions
One of the
zeros of the function f(x) = 2x2 – 5x - 3 is x = 3 because f(3) = 0, as shown in the screen above. This function has another zero.
![]()
![]()
A zero of a function is a value of the independent variable that makes the function zero. In other words, solutions to f(x) = 0 are the zeros of the function f.
![]()
![]()
1.1.1 Evaluate the function at other values of x until you find the other zero. When you have found the other zero, click here for the answer.
Guess and Check
When you tried several values until you found the second zero, you used a method called
The Guess and Check method can be used to find zeros (or roots)of a function. Use the "Guess and Check" method to find the zeros of a function as follows:
First guess a value for the independent variable and evaluate the function there.
If the value of the function is not zero, pick another value of the independent variable and evaluate the function again. Considering the results from previous guesses might improve your later guesses
Continue in this manner until a zero is found.
Guess and Check.
![]()
![]()
![]()
![]()
The Relationship Between Zeros and Factors
Many polynomial expressions, like 2x2 - 5x - 3, can be factored and there is a relationship between the zeros and the factors of the function.
1.1.2 Find the zeros of f(x) = 2x2 - 5x - 3 by factoring. Compare the zeros of the factors to the zeros of the function f(x) = 2x2 - 5x - 3 found earlier. Click here for the answer.
For polynomial functions. x = r is a zero of f if and only if x - r is a factor of f(x).