In this lesson, you will learn to use the Home screen and the TI-83 last answer feature, [Ans], to solve problems involving exponential expressions.

The TI-83 and TI-83 Plus have several ways in which an expression that contains repeated multiplication or an exponent may be evaluated. The examples below provide direction in using the calculator in different ways to evaluate expressions.

Doubling Bacteria Problem

Suppose that a colony of bacteria doubles in size every hour. If the colony contains 2000 bacteria at noon, how many bacteria will the colony contain at 2 p.m.? at 5 p.m.?

There are several ways to approach this problem numerically.

Entering Each Expression

One way is to analyze the problem is to enter each desired calculation separately, as shown in the problem below.

There are 2000 bacteria at the start, noon. Every hour the number of bacteria present doubles. That is, at the end of one hour (1 p.m.) there will be 4000 bacteria, at the end of two hours (2 p.m.) there will be 8000 bacteria, and so on.

The directions to evaluate expressions like 2000 x 2 and 4000 x 2 are shown below with the resulting screen. The first entry shows the original number of bacteria at noon.

1. Enter 2000 by pressing .
2. Enter 2000 x 2 by pressing .
3. Enter 4000 x 2 by pressing .

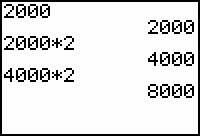
At the end of two hours (2 p.m.) there will be 8000 bacteria in the colony.

The Last Answer Feature

When an expression is evaluated successfully on the Home screen, the calculator stores the result in a storage area called ANS (last answer), which can be used in subsequent calculations. You can automatically place "Ans" as the first entry in the next command by pressing any of several function key, such as , , , or .

• Press to find the last result times 2, i.e., the population at 3 p.m.

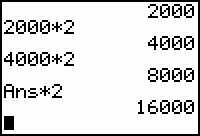
The variable "Ans" appeared when you pressed the key. The variable "Ans" contains the result of the most recent calculation, 8000, so Ans*2 is 16,000, which represents the number of bacteria after three hours (at 3 p.m.).

• Find the number of bacteria after four hours by pressing again.

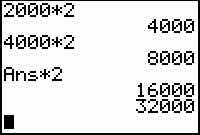
When you pressed the last command (Ans*2) was performed again and the result of 32,000 was displayed. "Ans" contained the value 16000 before the most recent was pressed and it was multiplied by 2.

Notice that the result of the command is displayed but the command is not shown. This should help you determine how many times you have performed Ans*2 by pressing . The number of bacteria present after 4 hours was 32,000, which is the last result.

• Find the population at 5 p.m by pressing again.

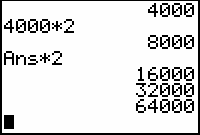
The population at 5 p.m. was 64,000.

Repeated Multiplication

Repeated multiplication may also be used to find the number of bacteria for specific hours since noon.
Notice that:

the population at 1 p.m. was 2000 x 2,

the population at 2 p.m. was (2000 x 2) x 2,

the population at 3 p.m. was [(2000 x 2) x 2] x 2.

In each case, the population is found by multiplying 2000 by 2 once for each hour since noon. That is, the population at 3 p.m. can be found by multiplying 2000 by 2 three times and the population at 5 p.m. can by found by multiplying 2000 by 2 five times, as shown in the screen below.

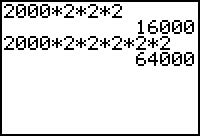
The Exponential Function Key

Repeated multiplication can be written using exponential notation. Another way to solve the problem is to use the exponential function key , which is in the last column of the fourth row.

• Reproduce the screen below by using the exponential function key.


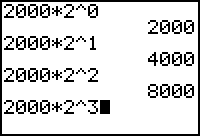
The screen shows that the population at noon (time 0) was 2000, at 1 p.m. was 4000, and at 2 p.m. was 8000. The last entry will produce the population at 3 p.m., three hours after the beginning time of noon.

Squares and Cubes

Using and 3 When using the calculator to square a number, you can either use the key or the key. To cube a number, you can either use the key or an exponent of 3, which can be found under the key menu, as shown below.

Use the TI-83 square function to find the population at 2 p.m.

• Enter the expression 2000*2² with the keystroke sequence
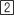
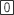
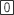
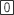
• Display the result by pressing .

Use the TI-83 cube function to evaluate the expression 2000*2³, the population at 3 p.m.

• Enter the expression 2000*2 by pressing
• Display the Math menu by pressing the key in the first column.

The cube function is the third item in this menu.


• Select the menu item 3:³ and paste the command to the Home screen.
• Press to perform the calculation.

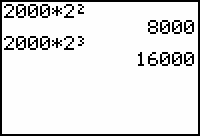
Negative Bases and Exponents

To enter an expression with a negative base, place parentheses around the base. Study the screen below. The first expression calculates -(2⁴), or -(2 x 2 x 2 x 2). The second expression calculates (-2)⁴, or (-2) x (-2) x (-2) x (-2).

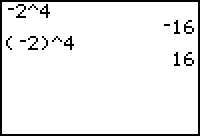
The calculator uses the rules for exponents and an exponent only applies to whatever immediately preceeds it. In the -2⁴ case, the exponent did not apply to the negative sign but in the (-2)⁴ case, -2 was raised to the fourth power because of the parentheses.