Page 16 - Activités algorithmiques avec Python en spécialité Mathématiques

Thème : fonctions
TI-83 Premium CE Edition Python TI-82 Advanced Edition Python
Niveau : spécialité maths Première + Terminale
Comment (presque) résoudre une équation
L. DIDIER & R. CABANE
Fiche méthode
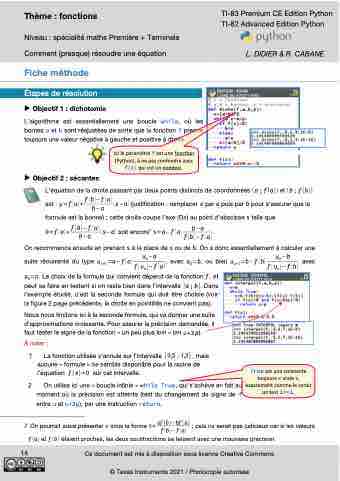
Étapes de résolution
▶ Objectif 1 : dichotomie
L’algorithme est essentiellement une boucle while, où les bornes a et b sont réajustées de sorte que la fonction f prenne toujours une valeur négative à gauche et positive à droite.
Ici le paramètre f est une fonction (Python), à ne pas confondre avec f(x) qui est un nombre.
▶ Objectif 2 : sécantess
L’équation de la droite passant par deux points distincts de coordonnées (a ; f (a)) et (b ; f (b))
est : y=f (a)+ f (b)−f (a)(x−a) (justification : remplacer x par a puis par b pour s’assurer que la b−a
formule est la bonne) ; cette droite coupe l’axe (Ox) au point d’abscisse s telle que
f (b)−f (a) b−a
b−a
f (b)−f (a)
(s−a)soitencore7 s=a−f(a)
On recommence ensuite en prenant s à la place de a ou de b. On a donc essentiellement à calculer une
0=f(a)+
.
, avec u0=b, ou bien un+1=b−f(b)
u −a suite récurrente du type un+1=a−f(a) n
u −b
n avec
f (un)−f (b)
f (un)−f (a)
u0=a. Le choix de la formule qui convient dépend de la fonction f , et
peut se faire en testant si on reste bien dans l’intervalle [a ; b]. Dans l’exemple étudié, c’est la seconde formule qui doit être choisie (voir la figure 2 page précédente, la droite en pointillés ne convient pas).
Nous nous limitons ici à la seconde formule, qui va donner une suite d’approximations croissante. Pour assurer la précision demandée, il faut tester le signe de la fonction « un peu plus loin » (en u+2 p).
À noter :
1
2
La fonction utilisée s’annule sur l’intervalle [0,5 ; 1,3] , mais aucune « formule » ne semble disponible pour la racine de l’équation f(x)=0 surcetintervalle.
True est une constante toujours « vraie »,
Onutiliseiciune«boucleinfinie»whileTrue,quis’achèveenfaitau exactementcommeleserait
moment où la précision est atteinte (test du changement de signe de f entre u et u+2p), par une instruction return.
un test 1==1.
7 On pourrait aussi présenter s sous la forme s=af (b)−bf (a) ; cela ne serait pas judicieux car si les valeurs f(b)−f(a)
f (a) et f (b) étaient proches, les deux soustractions se feraient avec une mauvaise précision.
14
Ce document est mis à disposition sous licence Creative Commons
© Texas Instruments 2021 / Photocopie autorisée