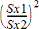Tuetut tilastotestit
Hypoteesitestejä on saatavilla Listat & taulukot -sovelluksesta. Katso lisätietoja näistä funktioista TI-Nspire™-käyttöoppaasta.
Joissakin tilastojen ohjatuissa toiminnoissa on valintaruutu Piirrä. Oletusarvoisesti ruutu ei ole valittuna. Valintamerkin lisääminen ruutuun luo Data & tilastot -sovelluksen työalueen ja tulokset piirtyvät työalueelle.
z -testi (zTest)
Suorittaa hypoteesitestin yhdelle tuntemattomalle perusjoukon keskiarvolle m, kun perusjoukon keskihajonta s tunnetaan. Se testaa nollahypoteesia H0: m=m0 yhteen seuraavista vaihtoehdoista.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Tätä testiä käytetään suurille perusjoukoille, joilla on normaalijakauma. Keskihajonta on tunnettava.
Tällä testillä voidaan määrittää, onko otoksen keskiarvon ja perusjoukon keskiarvon välinen ero tilastollisesti merkittävä, kun perusjoukon todellinen jakauma tunnetaan.
t -testi (tTest)
Testaa hypoteesia yhden tuntemattoman perusjoukon keskiarvoon m, kun perusjoukon keskihajontaa s ei tunneta. Se testaa nollahypoteesia H0: m=m0 yhteen seuraavista vaihtoehdoista.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Tämä testi on samanlainen kuin z-testi, mutta sitä käytetään, kun perusjoukko on pieni eikä normaalisti jakautunut. Tätä testiä käytetään useammin kuin z-testiä, koska tilastoissa esiintyy useammin pienen otoksen perusjoukkoja kuin suuria perusjoukkoja.
Tällä testillä voidaan määrittää, onko kahdella normaalijakauman perusjoukolla sama keskiarvo, tai kun halutaan määrittää, eroaako otoksen keskiarvo perusjoukon keskiarvosta huomattavasti, ja kun perusjoukon keskihajontaa ei tunneta.
2 otoksen z-testi (zTest_2Samp)
Testaa kahden perusjoukon (m1 ja m2) keskiarvojen samanlaisuutta riippumattomiin otoksiin perustuen, kun kummankin perusjoukon keskihajonnat (s1 ja s2) tunnetaan. Nollahypoteesia H0: m1=m2 testataan yhteen alla olevista vaihtoehdoista.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
2 otoksen t-testi (tTest_2Samp)
Testaa kahden perusjoukon (m1 ja m2) keskiarvojen samanlaisuutta riippumattomiin otoksiin perustuen, kun kumpaakaan perusjoukon keskihajontaa (s1 tai s2) ei tunneta. Nollahypoteesia H0: m1=m2 testataan yhteen alla olevista vaihtoehdoista.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
1 osuuden z-testi (zTest_1Prop)
Testaa tuntemattomien onnistumisten osuutta (prop). Syötearvoina annetaan onnistumisten määrä otoksessa x ja havaintojen määrä otoksessa n. 1-osuuden z-testi testaa nollahypoteesia H0: prop=p0 yhteen seuraavista vaihtoehdoista.
| • | Ha: propƒp0 |
| • | Ha: prop<p0 |
| • | Ha: prop>p0 |
Tämän testin avulla voidaan määrittää, onko otoksessa havaitun onnistumisen todennäköisyys merkittävästi erilainen kuin perusjoukon todennäköisyys vai johtuuko se näytteenottovirheestä, poikkeamasta vai muista tekijöistä.
2 osuuden z-testi (zTest_2Prop)
Laskee testin verraten kahden perusjoukon onnistumisen osuutta (p1 and p2). Syötearvoina annetaan onnistumisten määrä kummassakin otoksessa (x1 ja x2) sekä havaintojen määrä kummassakin otoksessa (n1 ja n2). 2-osuuden z-testi testaa nollahypoteesia H0: p1=p2 (käyttäen poolattua otossuhdetta Ç) yhteen seuraavista vaihtoehdoista.
| • | Ha: p1ƒp2 |
| • | Ha: p1<p2 |
| • | Ha: p1>p2 |
Tämän testin avulla voidaan määrittää, onko kahdessa otoksessa havaittu onnistumistodennäköisyys samanlainen.
c2GOF (c2GOF)
Suorittaa testin, jolla varmistetaan, että otoksen data on tiettyä jakaumaa vastaavasta perusjoukosta. c2 GOF voi esimerkiksi varmistaa, että otoksen data on normaalijakaumasta.
c2 2-suuntainen testi (c22way)
Laskee khi-neliötestin kaksisuuntaisen taulukon arvojen toisiinsa liittymisestä määritetyssä Havainto-matriisissa. Kaksisuuntaisen taulukon nollahypoteesi H0 on: rivimuuttujien ja sarakemuuttujien välillä ei ole yhteyttä. Vaihtoehtoinen hypoteesi on: muuttujat liittyvät toisiinsa.
2 otoksen F-testi (FTest_2Samp)
Laskee F--testin vertaillakseen kahta normaalin perusjoukon keskihajontaa (s1 ja s2). Perusjoukon keskiarvoja ja keskihajontoja ei tunneta. 2-otoksen F-testi, jossa käytetään otosten varianssien Sx12/Sx222 suhdetta, testaa nollahypoteesia H0: s1=s2 yhteen seuraavista vaihtoehdoista.
| • | Ha: s1ƒs2 |
| • | Ha: s1<s2 |
| • | Ha: s1>s2 |
Alla on 2- otoksen F-testin määritelmä.
|
Sx1, Sx2 |
= |
Otoksen keskihajonnoilla, joilla on n1N1 ja n2N1 vapausastetta df, vastaavasti. |
|
|
|
F-tilastollinen = |
|
df(x, n1N1, n2N1) |
= |
Fpdf( ), jonka vapausasteet df, n1N1 ja n2N1 |
|
p |
= |
raportoitu p-arvo |
2-otoksen F-testi vaihtoehtoiselle hypoteesille s1 >s2.
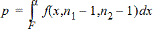
2-otoksen F-testi vaihtoehtoiselle hypoteesille s1 <s2.
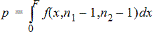
2-otoksen F-testi vaihtoehtoiselle hypoteesille s1ƒs2. Rajojen on täytettävä seuraavat vaatimukset:
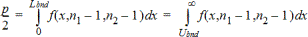
jossa: [Lbnd,Ubnd]=ala- ja ylärajat
F--tilastoa käytetään rajana, joka tuottaa pienimmän integraalin. Jäljelle jäävä raja valitaan siten, että saavutetaan edellisen integraalin samanlaisuussuhde.
Lineaarisen regression t-testi (LinRegtTest)
Laskee lineaarisen regression ja suorittaa t-testin kulmakertoimen b ja korrelaatiokertoimen r arvosta yhtälölle y=a+bx. Se testaa nollahypoteesia H0: b=0 (vastaavasti r=0) yhteen seuraavista vaihtoehdoista.
| • | Ha: bƒ0 ja rƒ0 |
| • | Ha: b<0 ja r<0 |
| • | Ha: b>0 ja r>0 |
Moninkertaiset regressiotestit (MultRegTests)
Laskee lineaarisen regression tietystä datasta ja antaa F-testin tilastot lineaarisuudelle.
Katso lisätietoja TI-Nspire™ -käyttöoppaasta.
ANOVA (ANOVA)
Laskee yksisuuntaisen varianssianalyysin 2–20 perusjoukon keskiarvojen vertaamiseksi. Näiden keskiarvojen vertailussa käytettävä ANOVA-menetelmä sisältää otosdatan vaihtelun analysoinnin. Nollahypoteesia H0: m1=m2=...=mk testataan vaihtoehtoon Ha: m1...mk eivät ole kaikki yhtä suuria.
ANOVA-testi on menetelmä, jolla määritetään, onko ryhmien välillä merkittävä ero verrattuna kunkin ryhmän sisällä esiintyvään eroon.
Tämän testin avulla voidaan määrittää, ilmaiseeko datan vaihtelu otosten välillä tilastollisesti merkittävää jonkin muun tekijän vaikutusta kuin itsensä datasarjojen sisällä olevan vaihtelun vaikutusta. Esimerkki: kuljetusyhtiön pakkauslaatikoiden hankkija haluaa arvioida kolmea eri pakkauslaatikon valmistajaa. Hän pyytää näytelaatikot kaikilta kolmelta toimittajalta. ANOVA-analyysin avulla hän voi määrittää, ovatko näyteryhmien väliset erot merkittäviä verrattuna kunkin näyteryhmän sisällä esiintyviin eroihin.
2-suuntainen ANOVA (ANOVA2way)
Laskee kaksisuuntaisen varianssianalyysin kahdesta 20:een perusjoukon keskiarvojen vertaamiseksi Tulosten yhteenveto tallentuu stat.results-muuttujaan.
Kaksisuuntainen ANOVA-varianssianalyysi tutkii kahden riippumattoman muuttujan vaikutuksia auttaen määrittämään, onko näillä vaikutusta riippuvaan muuttujaan. (Toisin sanoen, jos nämä kaksi riippumatonta muuttujaa ovat vuorovaikutuksessa, niiden yhdistetty vaikutus voi olla suurempi tai pienempi kuin jommankumman riippumattoman muuttujan vaikutus yhteensä.)
Tämän testin avulla voidaan arvioida vastaavanlaisia eroja kuin ANOVA-analyysissä, mutta tässä testissä on lisänä jokin muu potentiaalinen vaikutus. Jos jatkamme ANOVA-analyysin laatikkoesimerkkiä, kaksisuuntaisella ANOVA-analyysillä voitaisiin tutkia pakkauslaatikon materiaalin vaikutusta havaittuihin eroihin.
Vaihtoehtoisen hypoteesin (ƒ < >) valitseminen
Useimmat hypoteesien testaukseen tarkoitetut johdettujen tilastojen editorit pyytävät valitsemaan yhden kolmesta vaihtoehtoisesta hypoteesista.
| • | Ensimmäinen on vaihtoehtoinen hypoteesi ƒ, esimerkiksi mƒm0 z -testissä. |
| • | Toinen on vaihtoehtoinen < hypoteesi , esimerkiksi m1<m2 2-otoksen t -testissä. |
| • | Kolmas on vaihtoehtoinen > hypoteesi , esimerkiksi p1>p2 2- osuuden z -testissä. |
Valitse vaihtoehtoinen hypoteesi viemällä kohdistin sopivan vaihtoehdon kohdalle ja paina sen jälkeen Enter.
Poolatun toiminnon valitseminen
Poolattu (vain 2- otoksen t -testi ja 2- näytteen t -väli) määrittää, poolataanko varianssit laskutoimitusta varten.
| • | Valitse Ei, jos et halua poolata variansseja. Perusjoukon varianssit voivat olla erilaisia. |
| • | Valitse Kyllä, jos haluat poolata varianssit. Perusjoukon varianssien oletetaan olevan samanlaiset. |
Voit valita Poolaus-toiminnon valitsemalla vaihtoehdon Kyllä pudotuslistasta.