Esimerkki: Laske jakauma sovittaaksesi sen Normaali Pdf -jakaumamalliin.
| 1. | Napsauta sarakekaavan solua (toinen solu ylhäältä) sarakkeesta A. |
| 2. | Napsauta Tilastot > Jakaumat > Normaali Pdf jakaumamallin valitsemiseksi. |
Näytölle avautuu Normaali Pdf -valintaikkuna, jossa on argumenttien syöttö- tai valintakentät.
| 3. | Liiku kentissä Sarkain-painikkeella tarpeen mukaan ja anna kukin argumentti. Voit kirjoittaa arvot tai valita ne avattavasta valikosta. |
| - | X:n arvo: Napsauta pudotusvalikon nuolta ja valitse jokin tehtävän listoista määrittääksesi laskutoimitukseen x:n arvot. |
| - | Keskiarvo: Syötä keskiarvo tai klikkaa pudotusvalikon nuolta ja valitse muuttuja, joka sisältää keskiarvon. |
| - | Keskihajonta: Syötä keskihajonnan arvo tai valitse muuttuja, joka sisältää keskihajonnan. |
| 4. | Napsauttamalla Piirrä-valintaruutua voit nähdä jakauman piirrettynä Data & Tilastot -sovelluksessa. |
Huomaa: Piirrä-toiminto ei ole käytettävissä kaikille jakaumille.
| 5. | Klikkaa OK. |
Listat & Taulukot lisää kaksi saraketta: toinen sisältää vastausten nimet ja toinen niitä vastaavat arvot. Tulokset piirretään Data & Tilastot -sovelluksessa.
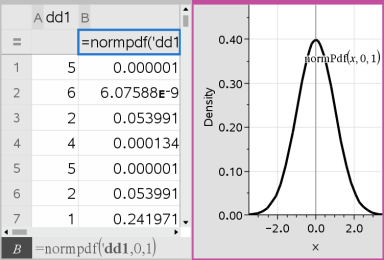
Huomaa: Tulokset on linkitetty lähdedataan. Jos esimerkiksi muutat arvoa sarakkeessa A, yhtälö päivittyy automaattisesti.
Listat & Taulukot -sovellus sisältää seuraavassa kuvatut jakaumatyypit. Katso lisätietoja näistä funktioista TI-Nspire™-käyttöoppaasta.
| • | Kun haluat laskea yhden jakauman tuloksen yhden arvon perusteella, syötä funktio yhteen soluun. |
| • | Kun haluat laskea jakauman tuloslistan arvolistan perusteella, syötä funktio yhteen sarakekaavan soluun. Tässä tapauksessa sinun tulee määrittää lista (sarake), joka sisältää arvot. Jakauma laskee vastaavan tuloksen jokaiselle listan arvolle. |
Huomaa: Toiminto on käytettävissä jakaumafunktioille, jotka tukevat piirtotoimintoa (normPDF, t PDF, χ² Pdf, ja F Pdf), vain siinä tapauksessa, että syötät jakaumafunktion kaavasoluun.
Normaali Pdf (normPdf)
Laskee todennäköisyystiheysfunktion (pdf) normaalijakaumalle määritetyllä x-arvolla. Keskiarvon oletusarvo on μ=0, ja keskihajonnan oletusarvo on σ=1. Todennäköisyystiheysfunktio (pdf) on:
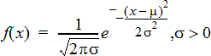
Tämän jakauman avulla määritetään tietyn arvon esiintymisen todennäköisyys normaalijakaumassa. Piirtotoiminto on käytettävissä, kun Normaali PDF -funktiota käytetään kaavasolusta.
Kun lasket jakaumia kaavasolusta, sinun on valittava pudotusvalikosta oikea lista, jotta tulokset ovat oikein. Jos lasket jakauman solusta, sinun on määritettävä x:lle lukuarvo. Jakauma laskee määrittämäsi arvon esiintymisen todennäköisyyden.
Normaali Cdf (normCdf)
Laskee normaalijakauman todennäköisyyden alarajan ja ylärajan väliltä määritetylle keskiarvolle, μ (oletusarvo=0) ja keskihajonnalle,s (oletusarvo=1). Voit varjostaa ala- ja ylärajan välisen alueen napsauttamalla Piirrä (varjosta alue) -valintaruutua. Alkuperäiseen alarajaan ja ylärajaan tehdyt muutokset päivittävät jakauman automaattisesti.
Tämän jakauman avulla voidaan määrittää minkä tahansa ala- ja ylärajan välillä olevan arvon esiintymisen todennäköisyys normaalijakaumassa. Se vastaa pinta-alan laskemista rajojen välissä olevan määritetyn normaalikäyrän alapuolelta.
Normaali käänteinen (invNorm)
Laskee käänteisen normaalijakauman kertymäfunktion annetulle alueelle normaalijakaumakäyrällä, joka on määritelty keskiarvolla μ ja keskihajonnalla s.
Tämän jakauman avulla voidaan määrittää datan x:n arvo vaihteluvälillä 0 - x<1, kun jakaantumiskäyrä tunnetaan.
t Pdf (tPdf)
Laskee todennäköisyystiheysfunktion (pdf) t-jakaumalle määritetyssä x-arvossa. df:n (vapausasteet) tulee olla 0. Todennäköisyystiheysfunktio (pdf) on:
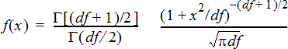
Tämän jakauman avulla voidaan määrittää arvon esiintymistodennäköisyys, kun perusjoukon keskihajonta ei ole tunnettu ja otoskoko on pieni. Piirtotoiminto on käytettävissä, kun t Pdf-funktiota käytetään kaavasolusta.
t Cdf (tCdf)
Laskee Student-t-jakauman todennäköisyyden alarajan ja ylärajan väliltä määritetyllä df-arvolla (vapausasteella). Voit varjostaa rajojen välisen alueen napsauttamalla Piirrä (Varjosta alue) -valintaruutua. Alkuperäiseen alarajaan ja ylärajaan tehdyt muutokset päivittävät jakauman automaattisesti.
Tämän jakauman avulla voidaan määrittää arvon esiintymistodennäköisyys ala- ja ylärajan rajaamalla välillä normaalijakauman funktiolle, kun perusjoukon keskihajonta ei ole tunnettu.
Käänteinen t (invt)
Laskee käänteisen kumulatiivisen t-jakauman todennäköisyysfunktion, joka on määritetty vapausasteella, df, tietylle käyrän alapuoliselle alueelle.
Tämän jakauman avulla voidaan määrittää datan esiintymistodennäköisyys alueella 0... x<1. Tätä funktiota käytetään, kun perusjoukon keskiarvoa ja/tai keskihajontaa ei tunneta.
c2 Pdf (c2 Pdf())
Laskee todennäköisyystiheysfunktion (pdf) c2 (khi-neliö) jakaumalle määritetyssä x-arvossa. df:n (vapausaste) tulee olla kokonaisluku 0. Todennäköisyystiheysfunktio (pdf) on:
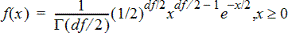
Tämän jakauman avulla voidaan määrittää tietyn arvon esiintymistodennäköisyys perusjoukosta, jossa on c2-jakauma. Piirtotoiminto on käytettävissä, kun c2 Pdf -funktiota käytetään kaavasolusta.
c2 Cdf (c2 Cdf())
Laskee c2 2 (khi-neliö) -jakauman todennäköisyyden alarajan ja ylärajan välillä annetulla df:llä (vapausasteella). Voit varjostaa ala- ja ylärajan välisen alueen napsauttamalla Piirrä Varjosta alue -valintaruutua. Alkuperäiseen alarajaan ja ylärajaan tehdyt muutokset päivittävät automaattisesti jakauman.
Tämän jakauman avulla voidaan määrittää arvon esiintymistodennäköisyys sellaisen perusjoukon määrättyjen rajojen sisällä, jossa on c2 -jakauma.
F Pdf (F Pdf())
Laskee todennäköisyystiheysfunktion (pdf) F-jakaumalle määritetyssä x-arvossa. osoittajan df:n (vapausaste) ja nimittäjän df:n tulee olla kokonaislukuja 0. Todennäköisyystiheysfunktio (pdf) on:
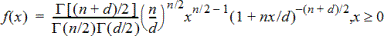
|
jossa |
n = osoittajan vapausasteet |
Tämän jakauman avulla voidaan määrittää todennäköisyys, jolla kahdella otoksella on sama varianssi. Piirtotoiminto on käytettävissä, kun F Pdf -funktiota noudetaan kaavasolusta.
F Cdf (F Cdf())
Laskee F-jakauman todennäköisyyden alarajan ja ylärajan välillä määritetylle dfOsoittajalle (vapausasteet) ja dfNimittäjälle. Voit varjostaa ala- ja ylärajan välisen alueen napsauttamalla Piirrä (varjosta alue) -valintaruutua. Alkuperäiseen alarajaan ja ylärajaan tehdyt muutokset päivittävät automaattisesti jakauman.
Tämän jakauman avulla voidaan määrittää todennäköisyys, jolla yksi havainto esiintyy ala- ja ylärajan välissä.
Binominen Pdf (binomPdf())
Laskee todennäköisyyden kohteessa x diskreetille binomijakaumalle määritetyllä toistojen määrällä (numtrials) ja onnistumistodennäköisyydellä (p) kussakin kokeessa. x voi olla kokonaisluku tai kokonaislukujen lista. 0{p{1 täytyy olla tosi. toistojen määrän tulee olla kokonaisluku > 0. Jos et määritä x:n arvoa, saat vastaukseksi todennäköisyyksien listan väliltä 0 ja toistojen määrä. Todennäköisyystiheysfunktio (pdf) on:
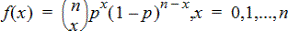
jossa n = toistojen määrä
Tämän jakauman avulla voidaan määrittää onnistumiseen/epäonnistumiseen päättyvän kokeen n onnistumistodennäköisyys. Voit käyttää tätä jakaumaa esimerkiksi ennustaessasi todennäköisyyttä saada kruuna kolikon viidennellä heitolla.
Binominen Cdf (binomCdf())
Laskee kumulatiivisen todennäköisyyden diskreetille binomiselle jakaumalle, jossa toistojen määrä on n ja jokaisen toiston onnistumistodennäköisyys on p.
Tämän jakauman avulla voidaan määrittää yhden kokeen onnistumistodennäköisyys ennen kaikkien kokeiden suorittamista. Esimerkiksi, jos kruuna voittaa kolikonheitossa ja aiot heittää kolikkoa 10 kertaa, tämä jakauma ennustaisi, että saat kruunan vähintään kerran 10 heitolla.
Käänteinen binomi (invBinom())
Johtuen kokeiden lukumäärästä (NumTrials) ja kunkin kokeen onnistumisen todennäköisyydestä (Prob) tämä funktio laskee onnistumisten minimimäärän, k, siten, että arvo, k, on suurempi tai yhtä suuri kuin annettu kumulatiivinen todennäköisyys (CumulativeProb).
Tämä jakauma on hyödyllinen määrättäessä binomisen cdf:n ylärajan syöttöä. Esimerkiksi, jos heität kolikkoa 10 kertaa, ja haluat todennäköisyyden saada x kruunaa tai vähemmän olevan suurempi kuin 75 %, tämä jakauma auttaa sinua määrittelemään, mikä x:n pitäisi olla.
Käänteinen Binomi suhteessa tekijään N (invBinomN())
Johtuen kunkin kokeen onnistumisen todennäköisyydestä (Prob), ja onnistumisten lukumäärästä (NumSuccess) tämä luku laskee kokeiden minimimäärän, N, siten, että arvo N on yhtä suuri tai pienempi kuin annettu kumulatiivinen todennäköisyys (CumulativeProb).
Tämä jakauma on hyödyllinen määrättäessä binomisen cdf:n kokeiden määrää. Esimerkiksi, jos heität kolikkoa monta kertaa, ja haluat kruunien lukumäärän olevan 6 tai vähemmän vähemmällä kuin 25 %:n todennäköisyydellä, tämä jakauma auttaa määräämään, kuinka monta kertaa kolikkoa pitäisi heittää.
Poissonin Pdf (poissPdf())
Laskee satunnaismuuttujan x todennäköisyyden diskreetille Poisson-jakaumalle määritetyllä keskiarvolla μ, jonka on oltava reaaliluku > 0. x voi olla kokonaisluku tai kokonaislukujen lista. Todennäköisyystiheysfunktio (pdf) on:
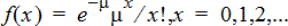
Tämän jakauman avulla voidaan määrittää todennäköisyys, jolla saadaan tietty määrä onnistumisia ennen kokeen aloittamista. Voit käyttää tätä laskutoimitusta esimerkiksi ennustaessasi kruunujen määrän, kun kolikkoa heitetään kahdeksan kertaa.
Poissonin Cdf (poissCdf())
Laskee kumulatiivisen todennäköisyyden diskreetille Poissonin jakaumalle, jolla on määritetty keskiarvo x.
Tämän jakauman avulla voidaan määrittää todennäköisyys, jolla tietty määrä onnistumisia tulee kokeen ylä- ja alarajojen välillä. Voit käyttää tätä laskutoimitusta esimerkiksi ennustaessasi, kuinka monta kertaa kolmannen ja kahdeksannen kolikonheiton välillä tulee kruuna.
Geometrinen Pdf (geomPdf())
Laskee diskreetin jakauman todennäköisyyden arvolle x, eli ensimmäisen onnistuneen kokeen järjestysnumeron kohdalla, määritetyllä onnistumistodennäköisyydellä p. 0{p{1 on oltava tosi. x voi olla kokonaisluku tai kokonaislukujen lista. Todennäköisyystiheysfunktio (pdf) on:
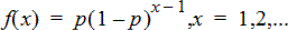
Tämän jakauman avulla voidaan määrittää todennäköisin kokeiden lukumäärä ennen onnistumista. Voit käyttää tätä laskutoimitusta esimerkiksi ennustaessasi, kuinka monta kertaa kolikkoa on heitettävä ennen kuin tulee kruuna.
Geometrinen Cdf (geomCdf())
Laskee kumulatiivisen geometrisen todennäköisyyden alarajalta ylärajalle määritetyllä onnistumistodennäköisyydellä p.
Tämän jakauman avulla voidaan määrittää ensimmäisen onnistumisen todennäköisyys, joka esiintyy yritysten 1–n välillä. Voit käyttää tätä laskutoimitusta esimerkiksi ennustaessasi todennäköisyyttä, että kruuna tulee heitoilla numero 1, 2, 3, ..., n.