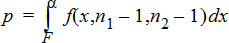Stat Tests
Supported Statistical Tests
Hypothesis tests are available from the Lists & Spreadsheets application. For more information regarding these functions, see the TI‑Nspire™ Reference Guide.
Some of the wizards for Stat Tests display a check box. By default, the box is not selected. Selecting the box creates a Data & Statistics work area on the page and plots the results in that work area.
z test (zTest)
Performs a hypothesis test for a single unknown population mean, m, when the population standard deviation, s, is known. It tests the null hypothesis H0: m=m0 against one of the alternatives below.
This test is used for large populations that are normally distributed. The standard deviation must be known.
This test is useful in determining if the difference between a sample mean and a population mean is statistically significant when you know the true deviation for a population.
t test (tTest)
Performs a hypothesis test for a single unknown population mean, m, when the population standard deviation, s, is unknown. It tests the null hypothesis H0: m=m0 against one of the alternatives below.
This test is similar to a z-test, but is used when the population is small and normally distributed. This test is used more frequently than the z-test because small sample populations are more frequently encountered in statistics than are large populations.
This test is useful in determining if two normally distributed populations have equal means, or when you need to determine if a sample mean differs from a population mean significantly and the population standard deviation is unknown.
2-Sample z Test (zTest_2Samp)
Tests the equality of the means of two populations (m1 and m2) based on independent samples when both population standard deviations (s1 and s2) are known. The null hypothesis H0: m1=m2 is tested against one of the alternatives below.
2-Sample t Test (tTest_2Samp)
Tests the equality of the means of two populations (m1 and m2) based on independent samples when neither population standard deviation (s1 or s2) is known. The null hypothesis H0: m1=m2 is tested against one of the alternatives below.
1-Prop z Test (zTest_1Prop)
Computes a test for an unknown proportion of successes (prop). It takes as input the count of successes in the sample x and the count of observations in the sample n. 1‑Prop z Test tests the null hypothesis H0: prop=p0 against one of the alternatives below.
This test is useful in determining if the probability of the success seen in a sample is significantly different from the probability of the population or if it is due to sampling error, deviation, or other factors.
2-Prop z Test (zTest_2Prop)
Computes a test to compare the proportion of successes (p1 and p2) from two populations. It takes as input the count of successes in each sample (x1 and x2) and the count of observations in each sample (n1 and n2). 2‑Prop z Test tests the null hypothesis H0: p1=p2 (using the pooled sample proportion Ç) against one of the alternatives below.
This test is useful in determining if the probability of success seen in two samples is equal.
c2GOF (c2GOF)
Performs a test to confirm that sample data is from a population that conforms to a specified distribution. For example, c2 GOF can confirm that the sample data came from a normal distribution.
c2 2-way Test (c22way)
Computes a chi-square test for association on the two-way table of counts in the specified Observed matrix. The null hypothesis H0 for a two-way table is: no association exists between row variables and column variables. The alternative hypothesis is: the variables are related.
2-Sample FTest (FTest_2Samp)
Computes an F‑test to compare two normal population standard deviations (s1 and s2). The population means and standard deviations are all unknown. 2‑Sample FTest, which uses the ratio of sample variances Sx12/Sx22, tests the null hypothesis H0: s1=s2 against one of the alternatives below.
Below is the definition for the 2‑Sample FTest.
|
Sx1, Sx2
|
=
|
Sample standard deviations having n1N1 and n2N1 degrees of freedom df, respectively.
|
|
F
|
=
|
F-statistic = 
|
|
df(x, n1N1, n2N1)
|
=
|
Fpdf( ) with degrees of freedom df, n1N1, and n2N1
|
|
p
|
=
|
reported p value
|
2‑Sample FTest for the alternative hypothesis s1 > s2.
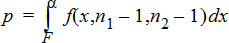
2‑Sample FTest for the alternative hypothesis s1 < s2.

2‑Sample FTest for the alternative hypothesis s1ƒs2. Limits must satisfy the following:

where: [Lbnd,Ubnd]=lower and upper limits
The F‑statistic is used as the bound producing the smallest integral. The remaining bound is selected to achieve the preceding integral’s equality relationship.
Linear Reg t Test (LinRegtTest)
Computes a linear regression on the given data and a t test on the value of slope b and the correlation coefficient r for the equation y=a+bx. It tests the null hypothesis H0: b=0 (equivalently, r=0) against one of the alternatives below.
Multiple Reg Tests (MultRegTest)
Computes a linear regression on the given data, and provides the F test statistic for linearity.
For more information, see the TI‑Nspire™ Reference Guide.
ANOVA (ANOVA)
Computes a one-way analysis of variance for comparing the means of 2 to 20 populations. The ANOVA procedure for comparing these means involves analysis of the variation in the sample data. The null hypothesis H0: m1=m2=...=mk is tested against the alternative Ha: not all m1...mk are equal.
The ANOVA test is a method of determining if there is a significant difference between the groups as compared to the difference occurring within each group.
This test is useful in determining if the variation of data from sample-to-sample shows a statistically significant influence of some factor other than the variation within the data sets themselves. For example, a box buyer for a shipping firm wants to evaluate three different box manufacturers. He obtains sample boxes from all three suppliers. ANOVA can help him determine if the differences between each sample group are significant as compared to the differences within each sample group.
ANOVA 2-Way (ANOVA2way)
Computes a two-way analysis of variance for comparing the means of two to 20 populations. A summary of results is stored in the stat.results variable.
The two-way ANOVA analysis of variance examines the effects of two independent variables and helps to determine if these interact with respect to the dependent variable. (In other words, if the two independent variables do interact, their combined effect can be greater than or less than the impact of either independent variable additively.)
This test is useful in evaluating differences similar to the ANOVA analysis but with the addition of another potential influence. To continue with the ANOVA box example, the two-way ANOVA might examine the influence of box material on the differences seen.
Selecting an Alternative Hypothesis (ƒ < >)
Most of the inferential stat editors for the hypothesis tests prompt you to select one of three alternative hypotheses.
|
•
|
The first is a ƒ alternative hypothesis, such as mƒm0 for the z Test. |
|
•
|
The second is a < alternative hypothesis, such as m1<m2 for the 2‑Sample t Test. |
|
•
|
The third is a > alternative hypothesis, such as p1>p2 for the 2‑Prop z Test. |
To select an alternative hypothesis, move the cursor to the appropriate alternative, and then press .
Selecting the Pooled Option
(2‑Sample t Test and 2‑Sample t Interval only) specifies whether the variances are to be pooled for the calculation.
|
•
|
Select if you do not want the variances pooled. Population variances can be unequal. |
|
•
|
Select if you want the variances pooled. Population variances are assumed to be equal. |
To select the option, select Yes from the drop-down list.