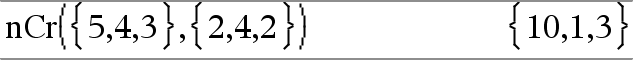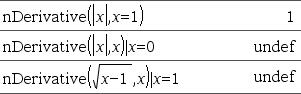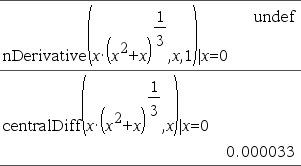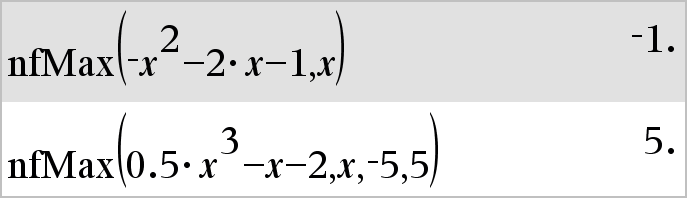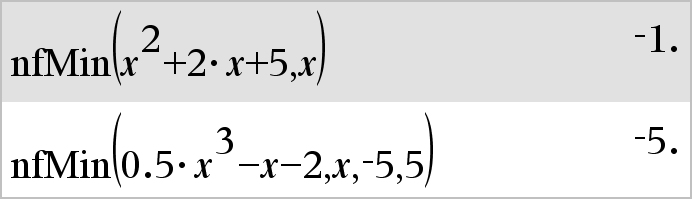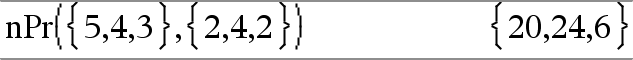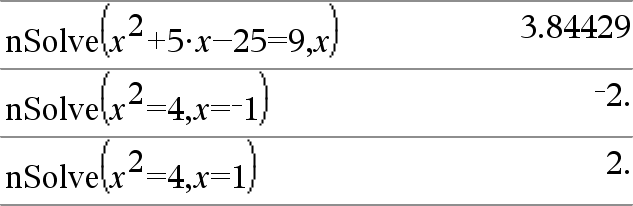|
/= knappar |
|
|
BoolesktUttr1
BooleskLista1
BooleskMatris1
Ger negation av en logisk Ger, för listor och matriser, jämförelser element för element. |
|
|
Heltal1
Jämför två reella heltal bit för bit med en Du kan skriva in heltalen i valfri talbas. För en binär eller hexadecimal inmatning måste du använda prefixet 0b respektive 0h. Utan prefix behandlas heltalen som decimala (bas 10). |
|
|
Katalog > |
|
|
nCr(Value1, Value2)Þuttryck För heltal Value1 och Value2 med Value1 | Value2 | 0 är nCr() antalet kombinationer av Value1 tagna Value2 åt gången. (Detta kallas också en binomial koefficient.) nCr(Value, 0)Þ1 nCr(Value, negInteger)Þ0 nCr(Value, posInteger)Þ Value·(ValueN1)... (ValueNposInteger+1)/posInteger! nCr(Value, nonInteger)Þexpression!/ ((ValueNnonInteger)!·nonInteger!) |
|
|
nCr(List1, List2)Þlista Ger en lista på kombinationer baserat på motsvarande elementpar i de två listorna. Argumenten måste ha samma liststorlek. |
|
|
nCr(Matrix1, Matrix2)Þmatris Ger en matris över kombinationer baserat på motsvarande elementpar i de två matriserna. Argumenten måste ha samma matrisstorlek. |
|
|
Katalog > |
|
|
Ger den numeriska derivatan beräknad med automatiska deriveringsmetoder. När Värde specificeras överstyr detta värde eventuella tidigare variabeltilldelningar eller aktuella ersättningar av typ “|” för variabeln. Om variabeln Var inte innehåller ett numeriskt värde måste du tillhandahålla Värde. Ordning för derivatan måste vara 1 eller 2. |
|
|
Studera exemplet till höger. Förstaderivatan av x·(x^2+x)^(1/3) för x=0 är lika med 0. Men eftersom förstaderivatan av deluttrycket (x^2+x)^(1/3) är odefinierat för x=0, och detta värde används för att beräkna derivatan av hela uttrycket, anger nDerivative() resultatet som odefinierat och visar ett varningsmeddelande. Om du stöter på denna begränsning, verifiera lösningen grafiskt. Du kan också prova att användacentralDiff(). |
|
|
Katalog > |
|
|
newList(numElements)Þlista Ger en lista med dimensionen på numElements. Varje element är noll. |
|
|
Katalog > |
|
|
newMat(numRows, numColumns)Þmatris Ger en matris med nollor med dimensionen numRows gånger numColumns. |
|
|
Katalog > |
|
|
nfMax(Expr, Var)Þvärde nfMax(Expr, Var, undrGräns)Þvärde nfMax(Expr, Var, undrGräns, övrGräns)Þvärde nfMax(Expr, Var) | undrGräns{Var{övrGränsÞvärde Ger ett möjligt numeriskt värde på variabeln Var där lokalt maximum för Expr inträffar. Om du inför undrGräns och övrGräns söker funktionen i det stängda intervallet [undrGräns,övrGräns] efter lokalt maximum. |
|
|
Katalog > |
|
|
nfMin(Expr, Var)Þvärde nfMin(Expr, Var, undrGräns)Þvärde nfMin(Expr, Var, undrGräns, övrGräns)Þvärde nfMin(Expr, Var) | undrGräns{Var{övrGränsÞvärde Ger ett möjligt numeriskt värde på variabeln Var där lokalt minimum för Expr inträffar. Om du inför undrGräns och övrGräns söker funktionen i det stängda intervallet [undrGräns,övrGräns] efter lokalt minimum. |
|
|
Katalog > |
|
|
nInt(Expr1, Var, Lower, Upper)Þuttryck Om integranden Expr1 inte innehåller någon variabel utöver Var, och om Lower och Upper är konstanter, positiv ˆ eller negativ ˆ, ger nInt() en uppskattning av ‰(Expr1, Var, Lower, Upper). Denna uppskattning är ett vägt genomsnitt av vissa sampelvärden hos integranden i intervallet Lower<Var<Upper. |
|
|
Målsättningen är sex signifikanta siffror. Den adaptiva algoritmen bestämmer när det verkar sannolikt att målet har uppnåtts, eller när det verkar osannolikt att ytterligare sampling ger en nämnvärd förbättring. En varning (“Questionable accuracy”) visas när det verkar som om målet inte har uppnåtts. |
|
|
Man kan kapsla in nInt() för att utföra multipel numerisk integrering. Integrationsgränser kan bero på integrationsvariabler utanför gränserna. |
|
|
Katalog > |
|
|
nom(effectiveRate,CpY)Þvärde Finansiell funktion som konverterar den årliga effektiva räntan effectiveRate till en nominell ränta, given av CpY som antalet sammansatta ränteperioder per år. effectiveRate måste vara ett reellt tal och CpY måste vara ett reellt tal > 0. Obs: Se även eff(), här. |
|
|
/= knappar |
|
|
BoolesktUttr1
BooleskLista1
BooleskMatris1
Ger negation av en logisk Ger, för listor och matriser, jämförelser element för element. |
|
|
Heltal1
Jämför två reella heltal bit för bit med en Du kan skriva in heltalen i valfri talbas. För en binär eller hexadecimal inmatning måste du använda prefixet 0b respektive 0h. Utan prefix behandlas heltalen som decimala (bas 10). |
|
|
Katalog > |
|
|
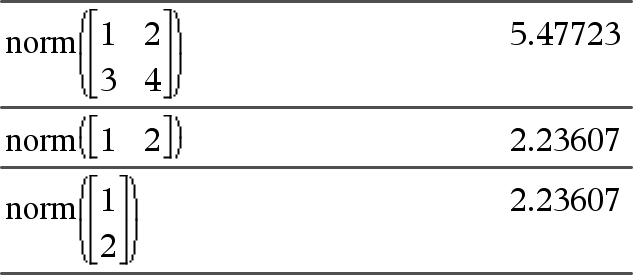
norm(Matrix)Þuttryck norm(Vector)Þuttryck Ger Frobenius norm. |
|
|
Katalog > |
|
|
normCdf(lowBound,upBound[,m[,s]])Þtal om lowBound och upBound är tal, lista om lowBound och upBound är listor Beräknar sannolikheten vid en normalfördelning mellan lowBound och upBound för specificerad m (förinställning=0) och s (förinställning=1).
|
|
|
Katalog > |
|
|
normPdf(XVal[,m[,s]])Þtal om XVal är ett tal, lista om XVal är en lista Beräknar värde hos täthetsfunktionen för normalfördelning vid ett specificerat XVal-värde för specificerad m och s. |
|
|
Katalog > |
|
|
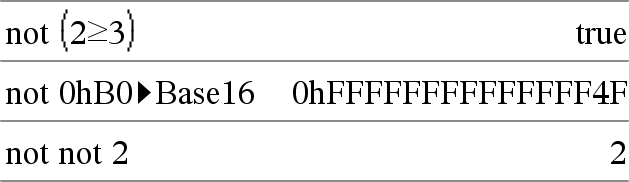
not BooleanExprÞBooleskt uttryck Ger en sann, falsk eller förenklad form av argumentet. |
|
|
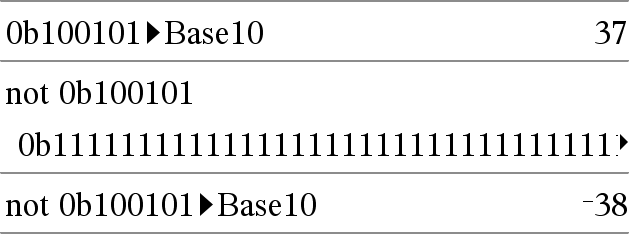
not Integer1Þheltal Ger ettkomplementet till ett reellt heltal. Internt omvandlas Integer1 till ett 64-bitars binärt tal. Värdet på varje bit växlas (0 blir 1 och vice versa) för ettans komplement. Resultaten visas enligt det inställda basläget. Du kan skriva in heltalet i valfri talbas. För en binär eller hexadecimal inmatning måste du använda prefixet 0b respektive 0h. Utan prefix behandlas heltalet som ett decimalt tal (bas 10). Om du skriver in ett decimalt heltal som är alltför stort för att anges i 64-bitars binär form används en symmetrisk modulooperation för att få ned värdet till lämplig nivå. För mer information, se 4Base2, här. |
I hexadecimalt basläge: Viktigt: Noll, inte bokstaven O.
I binärt basläge:
För att se hela resultatet, tryck på 5 och använd sedan 7 och 8 för att flytta markören. Obs: En binär inmatning kan ha upp till 64 siffror (exklusive prefixet 0b). En hexadecimal inmatning kan ha upp till 16 siffror. |
|
Katalog > |
|
|
nPr(Value1, Value2)Þuttryck För heltal Value1 och Value2 med Value1 | Value2 | 0 är nPr() antalet permutationer av Value1 saker tagna Value2 åt gången. nPr(Value, 0)Þ1 nPr(Value, negInteger)Þ1/((Value+1)·(Value+2)... (ValueNnegInteger)) nPr(Value, posInteger)ÞValue·(ValueN1)... (ValueNposInteger+1) nPr(Value, nonInteger)ÞValue! / (ValueNnonInteger)! |
|
|
nPr(List1, List2)Þlista Ger en lista på permutationer baserat på motsvarande elementpar i de två listorna. Argumenten måste ha samma liststorlek. |
|
|
nPr(Matrix1, Matrix2)Þmatris Ger en matris över permutationer baserat på motsvarande elementpar i de två matriserna. Argumenten måste ha samma matrisstorlek. |
|
|
Katalog > |
|
|
npv(InterestRate,CFO,CFList[,CFFreq]) Finansiell funktion som beräknar nettovärdet, dvs. summan av aktuella värden för kassainflöden och kassautflöden. Ett positivt resultat för npv indikerar en vinstgivande investering. InterestRate är räntan med vilken kassaflödena (kapitalanskaffningskostnaderna) diskonteras under en period. CF0 är det initiala kassaflödet vid tidpunkt 0 och måste vara ett reellt tal. CFList är en lista på kassaflödesbelopp efter det initiala kassaflödet CF0. CFFreq är en lista i vilken varje element specificerar frekvensen för ett grupperat (konsekutivt) kassaflödesbelopp, vilket är det motsvarande elementet i CFList. Förinställningen är 1. Om du vill mata in värden måste de vara positiva heltal < 10.000. |
|
|
Katalog > |
|
|
nSolve(Equation,Var[=Guess])Þtal eller fel_sträng nSolve(Equation,Var[=Guess],lowBound) Þtal eller fel_sträng nSolve(Equation,Var[=Guess],lowBound,upBound) Þtal eller fel_sträng nSolve(Equation,Var[=Guess]) | lowBound{Var{upBound Þtal eller fel_sträng Söker iterativt efter en ungefärlig reell numerisk lösning på Equation för dess variabel. Specificera variabeln som: variabel – eller – variabel = reellt tal Som exempel är x giltigt och likaså x=3. |
Obs: Om det finns flera lösningar kan du använda en gissning för att lättare hitta en viss lösning. |
|
nSolve() försöker att bestämma antingen en punkt där residualen är noll eller två relativt närliggande punkter där residualen har motsatta tecken och inte är överdrivet stor. Om detta inte kan uppnås med ett måttligt antal samplingspunkter erhålls strängen “no solution found”. |
|