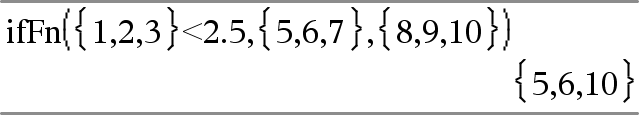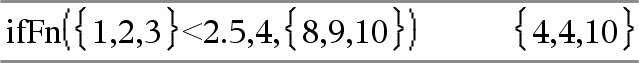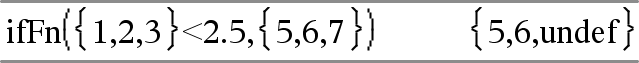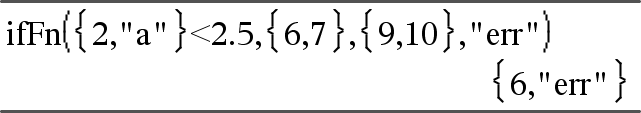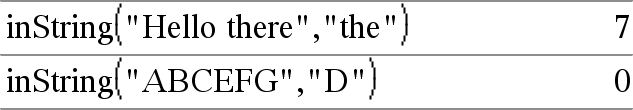identity(Integer) ⇒ matrix

Ger identitetsmatrisen med dimensionen Integer.

Integer måste vara positivt heltal.

If BoolesktUttr1 Then
       Block1
ElseIf BoolesktUttr2 Then
       Block2
⋮
ElseIf BoolesktUttrN Then
       BlockN
EndIf

Medger förgrening. If BooleanExpr1 utvärderar till sant och exekverar Block1. If BooleanExpr1 utvärderar till falskt, utvärderar BooleanExpr2, osv.

ifFn(BooleanExpr,Value_If_true [,Value_If_false [,Value_If_unknown]]) ⇒ uttryck, lista eller matris

Utvärderar det booleska uttrycket BooleanExpr (eller varje element från BooleanExpr ) och producerar ett resultat baserat på följande regler:

Obs: Om det förenklade påståendet BooleanExpr inbegriper en lista eller matris måste alla övriga list- eller matrisargument ha samma dimensioner, och resultatet får då samma dimensioner.

imag(Matrix1) ⇒ matris

Ger en matris med elementens imaginärdelar.

inString(srcString, subString[, Start]) ⇒ heltal

Ger teckenpositionen i strängen srcString där den första förekomsten av strängen subString börjar.

Start, om inkluderad, specificerar teckenpositionen inom srcString där sökningen börjar. Förinställning = 1 (det första tecknet i strängen srcString).

Återgår till noll om srcString inte innehåller subString eller om Start har en större längd än srcString.

int(Value) ⇒ heltal
int(List1) ⇒ lista
int(Matrix1) ⇒ matris

Ger det största heltalet som är mindre än eller lika med argumentet. Denna funktion är identisk med floor().

Argumentet kan vara ett reellt eller ett komplext tal.

Ger, för en lista eller matris, det största heltalet för varje element.

intDiv(Number1, Number2) ⇒ heltal
intDiv(List1, List2) ⇒ lista
intDiv(Matrix1, Matrix2) ⇒ matris

Ger heltalsdelen med tecken av (Number1 ÷ Number2).

Ger, för listor och matriser, heltalsdelen med tecken av (argument1 ÷ argument2) för varje elementpar.

Interpolera(xValue, xList, yList, yPrimeList) ⇒ lista

Denna funktion gör följande:

Förutsatt xList, yList=f(xList) och yPrimeList=f'(xList) används för en okänd funktion f en kubisk interpolant för att uppskatta funktionen f vid xValue. Det förutsätts att xList är en lista på monotont ökande eller minskande tal, men denna funktion kan ge ett värde även när listan inte uppfyller förutsättningarna. Denna funktion går igenom xList och söker ett intervall [xList[i], xList[i+1]] som innehåller xValue. Om funktionen hittar ett sådant intervall ger den ett interpolerat värde på f(xValue), annars ger den undef.

xList, yList och yPrimeList måste ha samma dimension ≥2 och innehålla uttryck som förenklas till tal.

xValue kan vara ett tal eller en lista av tal.

invχ2(Area,df)

invChi2(Area,df)

Beräknar den inversa kumulativa sannolikhetsfunktionen χ2 (chi-kvadrat) specificerad av frihetsgraden df för en given Area under kurvan.

invF(Area,dfNumer,dfDenom)

invF(Area,dfNumer,dfDenom)

beräknar den inversa kumulativa fördelningsfunktionen F specificerad av dfNumer och dfDenom för en given Area under kurvan.

invBinom(CumulativeProb,NumTrials,Prob,
OutputForm)⇒skalär eller matris

Baserat på antalet försök (NumTrials) och sannolikheten för önskat utfall av varje försök (Prob) ger denna funktion det minimala antalet lyckade utfall, k, så att den kumulativa sannolikheten,k, är större än eller lika med den givna kumulativa sannolikheten (CumulativeProb).

OutputForm=0, visar resultatet som en skalär (förvalt).

OutputForm=1, visar resultatet som en matris.

invBinomN(CumulativeProb,Prob,
NumSuccess,OutputForm)⇒skalär eller matris

Baserat på sannolikheten för lyckat utfall i varje försök (Prob) och antalet lyckade försök (NumSuccess) beräknar funktionen det minsta antalet försök, N, så att den kumulativa sannolikheten för x lyckade utfall är mindre eller lika med den givna kumulativ sannolikheten (CumulativeProb).

OutputForm=0, visar resultatet som en skalär (förvalt).

OutputForm=1, visar resultatet som en matris.

invNorm(Area[,μ[,σ]])

Beräknar den inversa kumulativa normalfördelningen för en given Area under normalfördelningskurvan specificerad av μ och σ.

invt(Area,df)

Beräknar den inversa kumulativa student-t- fördelningsfunktionen specificerad av frihetsgraden, df, för en given Area under kurvan.

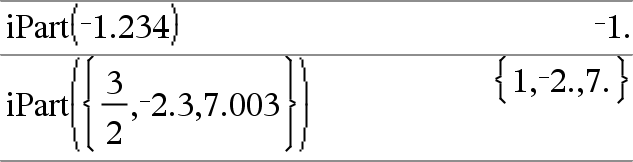
iPart(Number) ⇒ heltal
iPart(List1) ⇒ lista
iPart(Matrix1) ⇒ matris

Ger argumentets heltalsdel.

Ger, för listor och matriser, heltalsdelen för varje element.

Argumentet kan vara ett reellt eller ett komplext tal.

irr(CF0,CFList [,CFFreq]) ⇒ värde

Ekonomifunktion som beräknar internräntan på en investering.

CF0 är det initiala kassaflödet vid tidpunkt 0 och måste vara ett reellt tal.

CFList är en lista på kassaflödesbelopp efter det initiala kassaflödet CF0.

CFFreq är en frivillig lista i vilken varje element specificerar frekvensen för ett grupperat (konsekutivt) kassaflödesbelopp, vilket är det motsvarande elementet i CFList. Förinställningen är 1. Om du vill mata in värden måste de vara positiva heltal <10 000.

Obs: Se även mirr(), här.

isPrime(Number) ⇒ Booleskt konstantuttryck

Ger sant eller falskt för att indikera om number är ett heltal ≥2 som är jämnt delbart endast med sig självt och 1.

Om Number överskrider cirka 306 siffror och saknar faktorer ≤1021, visar isPrime(Number) ett felmeddelande.

Obs för att mata in exemplet: Se avsnittet Räknare i produkthandboken för instruktioner om hur du anger multiline-program och funktionsdefinitioner.

isVoid(Var) ⇒ Booleskt konstantuttryck
isVoid(Expr) ⇒ Booleskt konstantuttryck
isVoid(List) ⇒ lista av Booleska konstantuttryck

Ger sant eller falskt för att indikera huruvida argumentet är en tom datatyp.

För mer information om tomma element, se här.