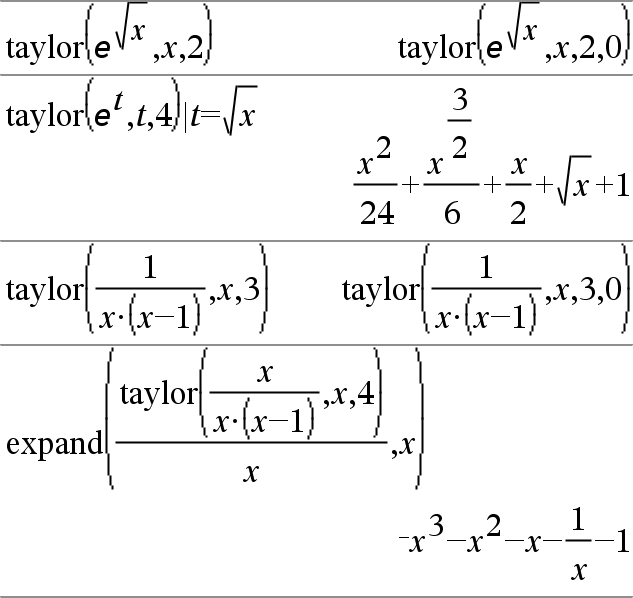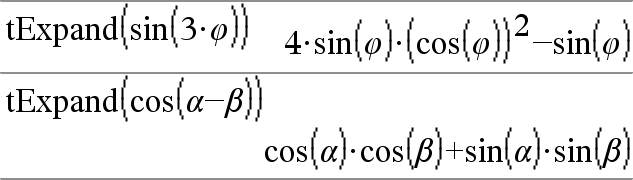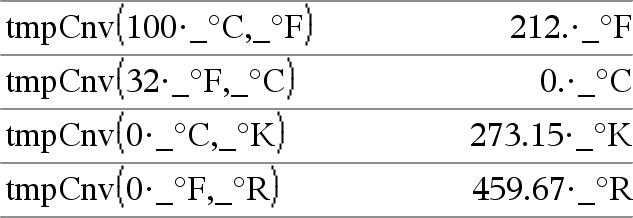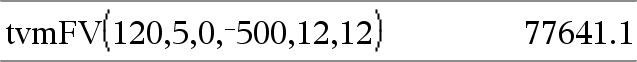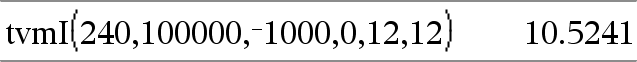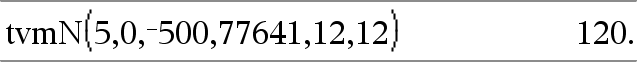|
Catalogue > |
|
|
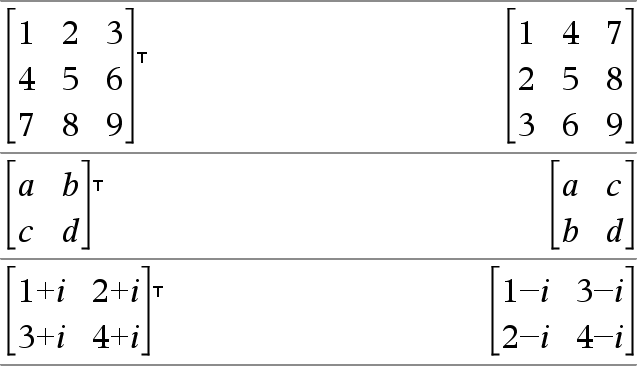
Matrix1TÞmatrice Donne la transposée de la conjuguée de Matrice1. Remarque : vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant @t. |
|
|
Touche µ |
|
|
tan(Expr1)Þexpression tan(Liste1)Þliste
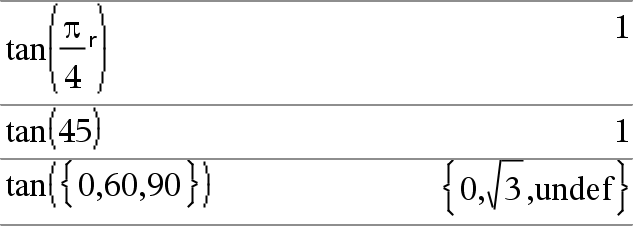
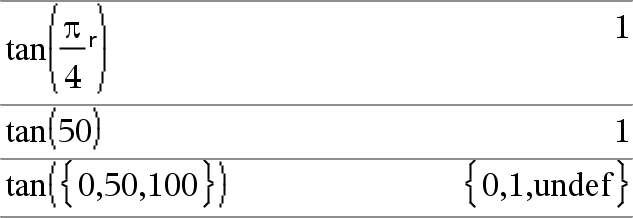
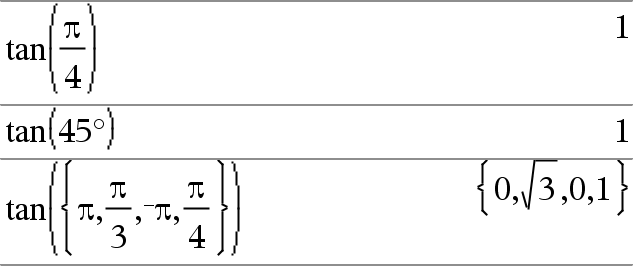
tan(List1) donne la liste des tangentes des éléments de Liste1. Remarque : l'argument est interprété comme mesure d'angle en degrés, en grades ou en radians, suivant le mode angulaire sélectionné. Vous pouvez utiliser ¡, G ou Rpour ignorer temporairement le mode Angle sélectionné. |
En mode Angle en degrés :
En mode Angle en grades :
En mode Angle en radians :
|
|
tan(matriceMatrice1)ÞmatriceCarrée Donne la tangente de la matrice matriceCarrée1. Ce calcul est différent du calcul de la tangente de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-vous à cos(). matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante. |
En mode Angle en radians :
|
|
Touche µ |
|
|
tan/(Expr1)Þexpression tan/(Liste1)Þliste
tan/(List1) donne la liste des arcs tangentes des éléments de Liste1. Remarque : donne le résultat en degrés, en grades ou en radians, suivant le mode angulaire utilisé. Remarque : vous pouvez insérer cette fonction à partir du clavier en entrant arctan(...). |
En mode Angle en degrés :
En mode Angle en grades :
En mode Angle en radians :
|
|
tan/(matriceCarrée1)ÞmatriceCarrée Donne l'arc tangente de la matrice matriceCarrée1. Ce calcul est différent du calcul de l'arc tangente de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-vous à cos(). matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante. |
En mode Angle en radians :
|
|
Catalogue > |
|
|
tangentLine(Expr1,Var,Point)Þexpression tangentLine(Expr1,Var=Point)Þexpression Donne la tangente de la courbe représentée par Expr1 au point spécifié par Var=Point. Assurez-vous de ne pas avoir affecté une valeur à la variable indépendante. Par exemple, si f1(x):=5 et x:=3, alors tangentLine(f1(x),x,2) donne « faux ». |
|
|
Catalogue > |
|
|
tanh(Expr1)Þexpression tanh(Liste1)Þliste
tanh(Liste1) donne la liste des tangentes hyperboliques des éléments de Liste1. |
|
|
tanh(matriceCarrée1)ÞmatriceCarrée Donne la tangente hyperbolique de la matrice matriceCarrée1. Ce calcul est différent du calcul de la tangente hyperbolique de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-vous à cos(). matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante. |
En mode Angle en radians :
|
|
Catalogue > |
|
|
tanh/(Expr1)Þexpression tanh/(Liste1)Þliste
tanh/(Liste1) donne la liste des arguments tangentes hyperboliques des éléments de Liste1. Remarque : vous pouvez insérer cette fonction à partir du clavier en entrant arctanh(...). |
En mode Format complexe Rectangulaire :
|
|
tanh/(matriceCarrée1)ÞmatriceCarrée Donne l'argument tangente hyperbolique de matriceCarrée1. Ce calcul est différent du calcul de l'argument tangente hyperbolique de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-vous à cos(). matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante. |
En mode Angle en radians et en mode Format complexe Rectangulaire :
Pour afficher le résultat entier, appuyez sur 5, puis utilisez les touches 7 et 8 pour déplacer le curseur. |
|
Catalogue > |
|
|
taylor(Expr1, Var, Ordre[, Point])Þexpression Donne le polynôme de Taylor demandé. Le polynôme comprend des termes non nuls de degrés entiers compris entre zéro et Ordre dans (Var moins Point). taylor() donne lui-même en l'absence de développement limité de cet ordre ou si l'opération exige l'utilisation d'exposants négatifs ou fractionnaires. Utilisez des opérations de substitution et/ou de multiplication temporaire par une puissance de (Var moins Point) pour déterminer un développement généralisé. Par défaut, la valeur de Point est égale à zéro et il s'agit du point de développement. |
|
|
Catalogue > |
|
|
tCdf(LimitInf,LimitSup,df)Þnombre si LimitInf et LimitSup sont des nombres, liste si LimitInf et LimitSup sont des listes Calcule la fonction de répartition de la loi de Student-t à df degrés de liberté entre LimitInf et LimitSup. Pour P(X { upBound), définissez lowBound = .ˆ. |
|
|
Catalogue > |
|
|
tCollect(Expr1)Þexpression Donne une expression dans laquelle les produits et les puissances entières des sinus et des cosinus sont convertis en une combinaison linéaire de sinus et de cosinus de multiples d'angles, de sommes d'angles et de différences d'angles. La transformation convertit les polynômes trigonométriques en une combinaison linéaire de leurs harmoniques. Quelquefois, tCollect() permet d'atteindre vos objectifs lorsque la simplification trigonométrique n'y parvient pas. tCollect() fait l'inverse des transformations effectuées par tExpand(). Parfois, l'application de tExpand() à un résultat de tCollect(), ou vice versa, permet en deux étapes de simplifier une expression. |
|
|
Catalogue > |
|
|
tExpand(Expr1)Þexpression Donne une expression dans laquelle les sinus et les cosinus de multiples entiers d'angles, de sommes d'angles et de différences d'angles sont développés. En raison de la présence de l'identité (sin(x))2+(cos(x))2=1, il existe plusieurs résultats équivalents possibles. Par conséquent, un résultat peut différer d'un autre résultat affiché dans d'autres publications. Quelquefois, tExpand() permet d'atteindre vos objectifs lorsque le développement trigonométrique n'y parvient pas. tExpand() tend à faire l'inverse des transformations effectuées par tCollect(). Parfois, l'application de tCollect() à un résultat de tExpand(), ou vice versa, permet en deux étapes de simplifier une expression. Remarque : la conversion en degrés par p/180 peut interférer avec la capacité de tExpand() de reconnaître les formes pouvant être développées. Pour de meilleurs résultats, tExpand() doit être utilisé en mode Angle en radians. |
|
|
Catalogue > |
|||||||
|
Commande de programmation : Marque une pause dans l'exécution du programme et affiche la chaîne de caractères chaîneinvite dans une boîte de dialogue. Lorsque l'utilisation sélectionne OK, l'exécution du programme se poursuit. L'argument optionnel IndicAff peut correspondre à n'importe quelle expression.
Si le programme nécessite une réponse saisie par l'utilisateur, voir Remarque : vous pouvez utiliser cette commande dans un programme créé par l'utilisateur, mais pas dans une fonction. |
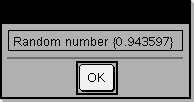
Définissez un programme qui marque une pause afin d'afficher cinq nombres aléatoires dans une boîte de dialogue. Dans le modèle Prgm...EndPrgm, validez chaque ligne en appuyant sur @ à la place de ·. Sur le clavier de l'ordinateur, maintenez enfoncée la touche Alt tout en appuyant sur Entrée.
Define text_demo()=Prgm For i,1,5 strinfo:=”Random number “ & string(rand(i)) Text strinfo EndFor EndPrgm
Exécutez le programme : text_demo()
Exemple de boîte de dialogue :
|
|
Voir If, ici. |
|
|
|
|
|
Catalogue > |
|
|
tInterval Liste[,Fréq[,CLevel]] (Entrée de liste de données) tInterval v,sx,n[,CLevel] (Récapitulatif des statistiques fournies en entrée) Calcule un intervalle de confiance t. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir ici.) Pour plus d'informations concernant les éléments vides dans une liste, reportez-vous à “Éléments vides”, ici. |
|
|
Variable de sortie |
Description |
|
stat.CLower, stat.CUpper |
Intervalle de confiance pour une moyenne inconnue de population |
|
stat.x |
Moyenne d'échantillon de la série de données suivant la loi normale aléatoire |
|
stat.ME |
Marge d'erreur |
|
stat.df |
Degrés de liberté |
|
stat.sx |
Écart-type d’échantillon |
|
stat.n |
Taille de la série de données avec la moyenne d'échantillon |
|
Catalogue > |
|
|
tInterval_2Samp Liste1,Liste2[,Fréq1[,Freq2[,CLevel[,Group]]]] (Entrée de liste de données) tInterval_2Samp v1,sx1,n1,v2,sx2,n2[,CLevel[,Group]] (Récapitulatif des statistiques fournies en entrée) Calcule un intervalle de confiance t sur 2 échantillons. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir ici.) Group=1 met en commun les variances ; Groupe=0 ne met pas en commun les variances. Pour plus d'informations concernant les éléments vides dans une liste, reportez-vous à “Éléments vides”, ici. |
|
|
Variable de sortie |
Description |
|
stat.CLower, stat.CUpper |
Intervalle de confiance contenant la probabilité du niveau de confiance de la loi |
|
stat.x1-x2 |
Moyennes d'échantillon des séries de données suivant la loi normale aléatoire |
|
stat.ME |
Marge d'erreur |
|
stat.df |
Degrés de liberté |
|
stat.x1, stat.x2 |
Moyennes d'échantillon des séries de données suivant la loi normale aléatoire |
|
stat.sx1, stat.sx2 |
Écarts-types d'échantillon pour Liste 1 et Liste 2 |
|
stat.n1, stat.n2 |
Nombre d'échantillons dans les séries de données |
|
stat.sp |
Écart-type du groupe. Calculé lorsque Group = YES. |
|
Catalogue > |
|
|
tmpCnv(Expr_¡unitéTemp1, _¡unitéTemp2) Þexpression _¡unitéTemp2 Remarque : vous pouvez insérer cette fonction à partir du clavier de l'ordinateur en entrant deltaTmpCnv(...). Convertit un écart de température (la différence entre deux valeurs de température) spécifié par Expr d'une unité à une autre. Les unités de température utilisables sont : _¡CCelsius _¡FFahrenheit _¡KKelvin _¡RRankine Pour taper ¡, sélectionnez ce symbole dans le Jeu de symboles ou entrez @d. Pour taper _, appuyez sur /_. Par exemple, 100_¡C donne 212_¡F. Pour convertir un écart de température, utilisez @tmpCnv(). |
Remarque : vous pouvez utiliser le Catalogue pour sélectionner des unités de température. |
|
Catalogue > |
|
|
@tmpCnv(Expr_¡unitéTemp1, _¡unitéTemp2) Þexpression _¡unitéTemp2 Convertit un écart de température (la différence entre deux valeurs de température) spécifié par Expr d'une unité à une autre. Les unités de température utilisables sont : _¡CCelsius _¡FFahrenheit _¡KKelvin _¡RRankine Pour taper ¡, sélectionnez-le dans les symboles du Catalogue. Pour taper _, appuyez sur /_. Des écarts de 1_¡C et 1_¡K représentent la même grandeur, de même que 1_¡F et 1_¡R. Par contre, un écart de 1_¡C correspond au 9/5 d'un écart de 1_¡F. Par exemple, un écart de 100_¡C (de 0_¡C à 100_¡C) est équivalent à un écart de 180_¡F. Pour convertir une valeur de température particulière au lieu d'un écart, utilisez la fonction tmpCnv(). |
Pour taper @, sélectionnez-le dans les symboles du Catalogue.
Remarque : vous pouvez utiliser le Catalogue pour sélectionner des unités de température. |
|
Catalogue > |
|
|
tPdf(ValX,df)Þnombre si ValX est un nombre, liste si ValX est une liste Calcule la densité de probabilité (pdf) de la loi de Student-t à df degrés de liberté en ValX. |
|
|
Catalogue > |
|
|
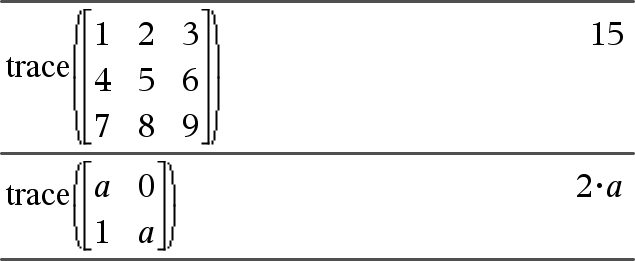
trace(matriceCarrée)Þexpression Donne la trace (somme de tous les éléments de la diagonale principale) de matriceCarrée. |
|
|
Catalogue > |
|
|
Try Exécute bloc1, à moins qu'une erreur ne se produise. L'exécution du programme est transférée au bloc2 si une erreur se produit au bloc1. La variable système errCode contient le numéro d'erreur pour permettre au programme de procéder à une reprise sur erreur. Pour obtenir la liste des codes d'erreur, voir la section « Codes et messages d'erreur », ici. bloc1 et bloc2 peuvent correspondre à une instruction unique ou à une série d'instructions séparées par le caractère “:”. Remarque pour la saisie des données de l’exemple : Pour obtenir des instructions sur la saisie des définitions de fonction ou de programme sur plusieurs lignes, consultez la section relative à la calculatrice dans votre guide de produit. |
|
|
Pour voir fonctionner les commandes Try, ClrErr et PassErr, saisissez le programme eigenvals() décrit à droite. Exécutez le programme en exécutant chacune des expressions suivantes.
|
Définition du programme eigenvals(a,b)=Prgm © Le programme eigenvals(A,B) présente les valeurs propres A·B Try Disp "A= ",a Disp "B= ",b Disp " " Disp "Eigenvalues of A·B are:",eigVl(a*b) Else If errCode=230 Then Disp "Error: Product of A·B must be a square matrix" ClrErr Else PassErr EndIf EndTry EndPrgm
|
|
Catalogue > |
|
|
tTest m0,Liste[,Fréq[,Hypoth]] (Entrée de liste de données) tTest m0,x,sx,n,[Hypoth] (Récapitulatif des statistiques fournies en entrée) Teste une hypothèse pour une moyenne inconnue de population m quand l'écart-type de population s est inconnu. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir ici.) Test de H0 : m = m0, en considérant que : Pour Ha : m < m0, définissez Hypoth<0 Pour Ha : m ƒ m0 (par défaut), définissez Hypoth=0 Pour Ha : m > m0, définissez Hypoth>0 Pour plus d'informations concernant les éléments vides dans une liste, reportez-vous à “Éléments vides”, ici. |
|
|
Variable de sortie |
Description |
|
stat.t |
(x N m0) / (stdev / sqrt(n)) |
|
stat.PVal |
Plus petit seuil de signification permettant de rejeter l'hypothèse nulle |
|
stat.df |
Degrés de liberté |
|
stat.x |
Moyenne d'échantillon de la série de données dans Liste |
|
stat.sx |
Écart-type d'échantillon de la série de données |
|
stat.n |
Taille de l'échantillon |
|
Catalogue > |
|
|
tTest_2Samp Liste1,Liste2[,Fréq1[,Fréq2[,Hypoth[,Group]]]] (Entrée de liste de données) tTest_2Samp v1,sx1,n1,v2,sx2,n2[,Hypoth[,Group]] (Récapitulatif des statistiques fournies en entrée) Effectue un test t sur deux échantillons. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir ici.) Test de H0 : m1 = m2, en considérant que : Pour Ha : m1< m2, définissez Hypoth<0 Pour Ha : m1ƒ m2 (par défaut), définissez Hypoth=0 Pour Ha : m1> m2, définissez Hypoth>0 Group=1 met en commun les variances Group=0 ne met pas en commun les variances Pour plus d'informations concernant les éléments vides dans une liste, reportez-vous à “Éléments vides”, ici. |
|
Variable de sortie |
Description |
|
stat.t |
Valeur normale type calculée pour la différence des moyennes |
|
stat.PVal |
Plus petit seuil de signification permettant de rejeter l'hypothèse nulle |
|
stat.df |
Degrés de liberté des statistiques t |
|
stat.x1, stat.x2 |
Moyennes d'échantillon des séquences de données dans Liste 1 et Liste 2 |
|
stat.sx1, stat.sx2 |
Écarts-types d'échantillon des séries de données dans Liste 1 et Liste 2 |
|
stat.n1, stat.n2 |
Taille des échantillons |
|
stat.sp |
Écart-type du groupe. Calculé lorsque Group=1. |
|
Catalogue > |
|
|
tvmFV(N,I,PV,Pmt,[PpY],[CpY],[PmtAt])Þvaleur Fonction financière permettant de calculer la valeur acquise de l'argent. Remarque : Les arguments utilisés dans les fonctions TVM sont décrits dans le tableau des arguments TVM, ici. Voir également amortTbl(), ici. |
|
|
Catalogue > |
|
|
tvmI(N,PV,Pmt,FV,[PpY],[CpY],[PmtAt])Þvaleur Fonction financière permettant de calculer le taux d'intérêt annuel. Remarque : Les arguments utilisés dans les fonctions TVM sont décrits dans le tableau des arguments TVM, ici. Voir également amortTbl(), ici. |
|
|
Catalogue > |
|
|
tvmN(I,PV,Pmt,FV,[PpY],[CpY],[PmtAt])Þvaleur Fonction financière permettant de calculer le nombre de périodes de versement. Remarque : Les arguments utilisés dans les fonctions TVM sont décrits dans le tableau des arguments TVM, ici. Voir également amortTbl(), ici. |
|
|
Catalogue > |
|
|
tvmPmt(N,I,PV,FV,[PpY],[CpY],[PmtAt])Þvaleur Fonction financière permettant de calculer le montant de chaque versement. Remarque : Les arguments utilisés dans les fonctions TVM sont décrits dans le tableau des arguments TVM, ici. Voir également amortTbl(), ici. |
|
|
Catalogue > |
|
|
tvmPV(N,I,Pmt,FV,[PpY],[CpY],[PmtAt])Þvaleur Fonction financière permettant de calculer la valeur actuelle. Remarque : Les arguments utilisés dans les fonctions TVM sont décrits dans le tableau des arguments TVM, ici. Voir également amortTbl(), ici. |
|
|
Description |
Type de données |
|
|
N |
Nombre de périodes de versement |
nombre réel |
|
I |
Taux d'intérêt annuel |
nombre réel |
|
PV |
Valeur actuelle |
nombre réel |
|
Pmt |
Montant des versements |
nombre réel |
|
FV |
Valeur acquise |
nombre réel |
|
PpY |
Versements par an, par défaut=1 |
Entier> 0 |
|
CpY |
Nombre de périodes de calcul par an, par défaut=1 |
Entier> 0 |
|
PmtAt |
Versement dû à la fin ou au début de chaque période, par défaut=fin |
entier (0=fin, 1=début) |
* Ces arguments de valeur temporelle de l'argent sont similaires aux noms des variables TVM (comme tvm.pv et tvm.pmt) utilisées par le solveur finance de l'application Calculator.Cependant, les fonctions financières n'enregistrent pas leurs valeurs ou résultats dans les variables TVM.
|
Catalogue > |
|
|
TwoVar X, Y[, [Fréq] [, Catégorie, Inclure]] Calcule des statistiques pour deux variables. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir ici.) Toutes les listes doivent comporter le même nombre de lignes, à l'exception de Inclure. X et Y sont des listes de variables indépendantes et dépendantes. Fréq est une liste facultative de valeurs qui indiquent la fréquence. Chaque élément dans Fréq correspond à une fréquence d'occurrence pour chaque couple X et Y. Par défaut, cette valeur est égale à 1. Tous les éléments doivent être des entiers | 0. Catégorie est une liste de codes de catégories pour les couples X et Y correspondants. Inclure est une liste d'un ou plusieurs codes de catégories. Seuls les éléments dont le code de catégorie figure dans cette liste sont inclus dans le calcul. Tout élément vide dans les listes X, Fréq ou Catégorie a un élément vide correspondant dans l'ensemble des listes résultantes. Tout élément vide dans les listes X1 à X20 a un élément vide correspondant dans l'ensemble des listes résultantes. Pour plus d'informations concernant les éléments vides, reportez-vous à la ici. |
|
|
Variable de sortie |
Description |
|
stat.v |
Moyenne des valeurs x |
|
stat.Gx |
Somme des valeurs x |
|
stat.Gx2 |
Somme des valeurs x2 |
|
stat.sx |
Écart-type de l'échantillon de x |
|
stat.sx |
Écart-type de la population de x |
|
stat.n |
Nombre de points de données |
|
stat.w |
Moyenne des valeurs y |
|
stat.Gy |
Somme des valeurs y |
|
stat.Gy2 |
Somme des valeurs y2 |
|
stat.sy |
Écart-type de y dans l'échantillon |
|
stat.sy |
Écart-type de population des valeurs de y |
|
stat.Gxy |
Somme des valeurs x·y |
|
stat.r |
Coefficient de corrélation |
|
stat.MinX |
Minimum des valeurs de x |
|
stat.Q1X |
1er quartile de x |
|
stat.MedianX |
Médiane de x |
|
stat.Q3X |
3ème quartile de x |
|
stat.MaxX |
Maximum des valeurs de x |
|
stat.MinY |
Minimum des valeurs de y |
|
stat.Q1Y |
1er quartile de y |
|
stat.MedY |
Médiane de y |
|
stat.Q3Y |
3ème quartile de y |
|
stat.MaxY |
Maximum des valeurs y |
|
stat.G(x-v)2 |
Somme des carrés des écarts par rapport à la moyenne de x |
|
stat.G(y-w)2 |
Somme des carrés des écarts par rapport à la moyenne de y |