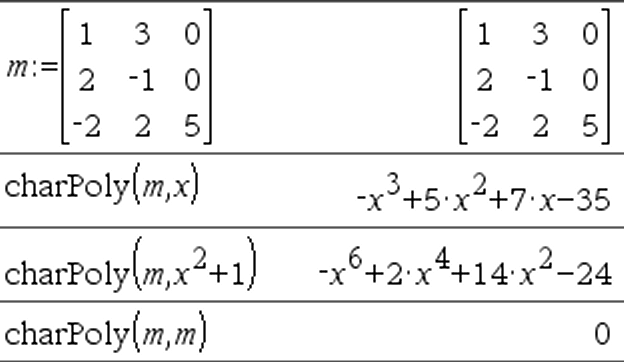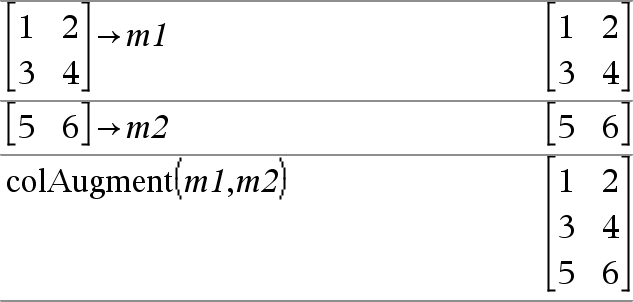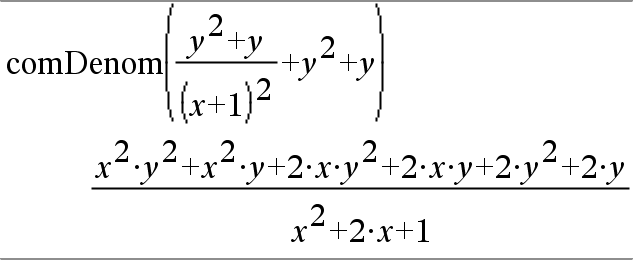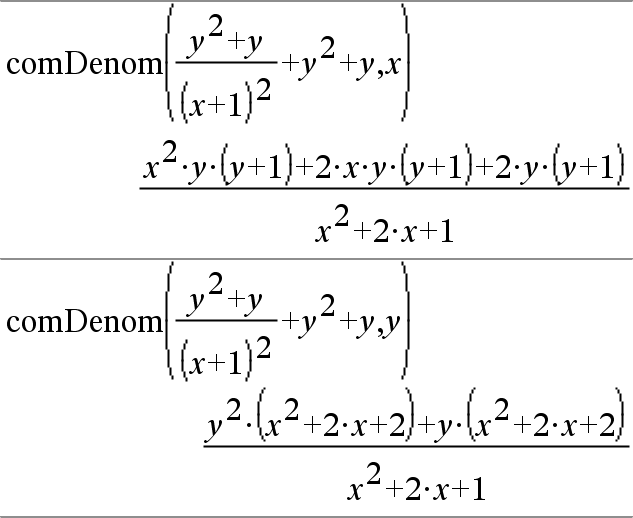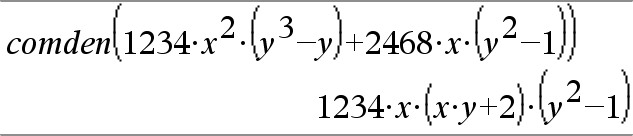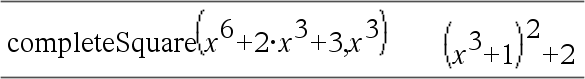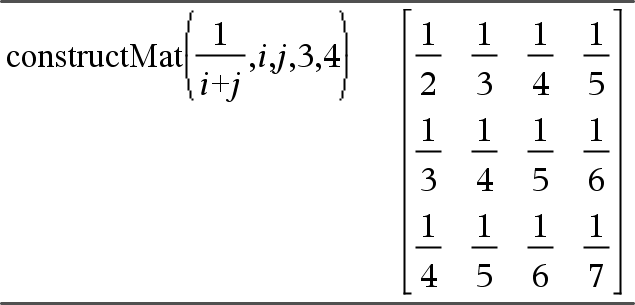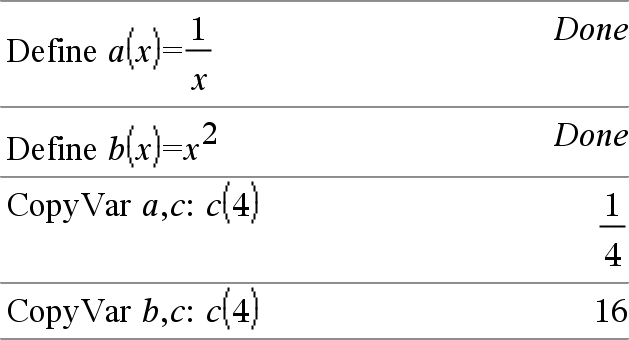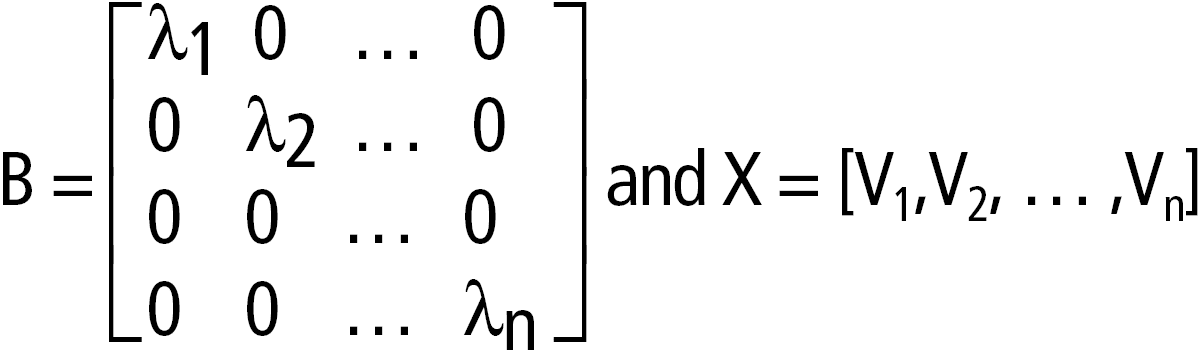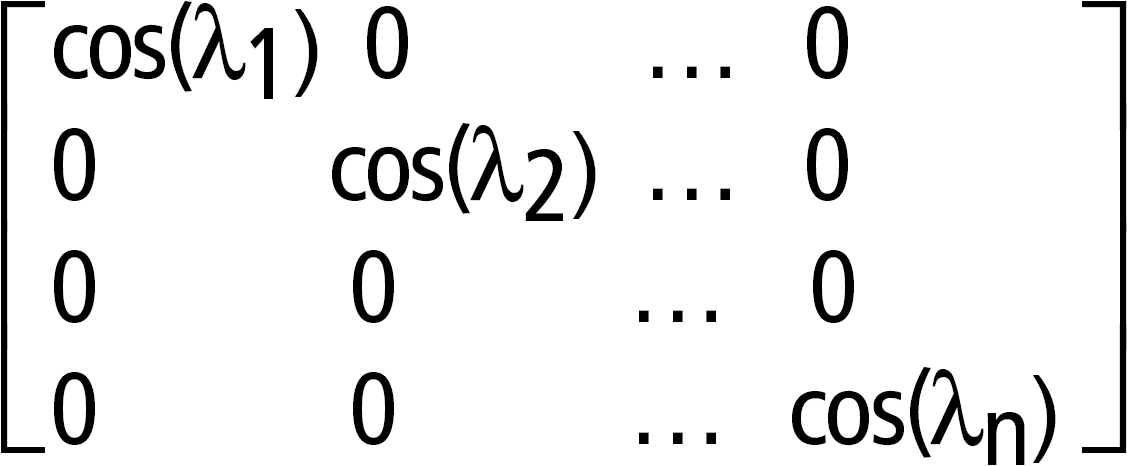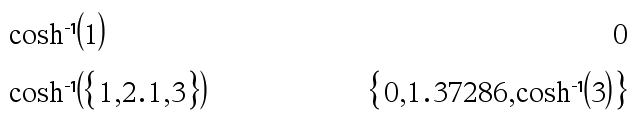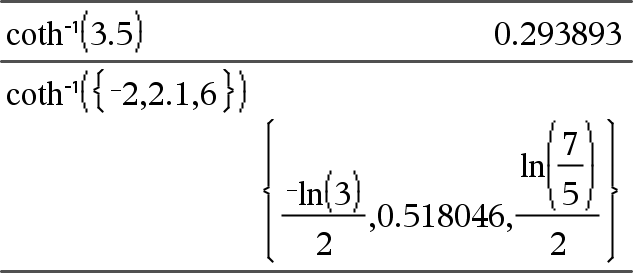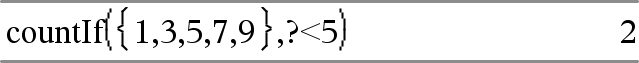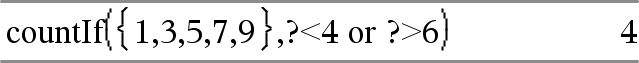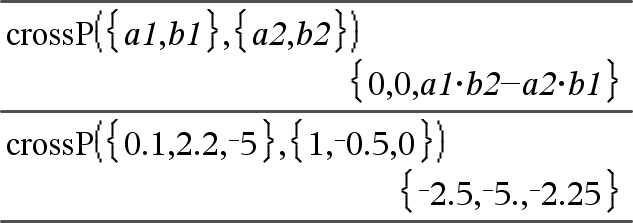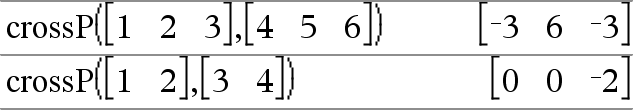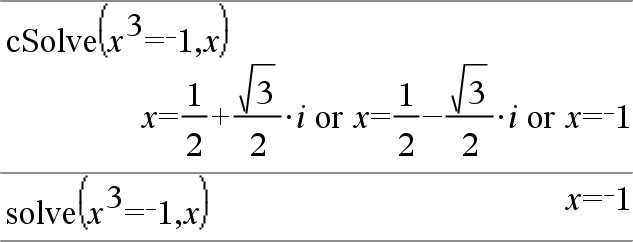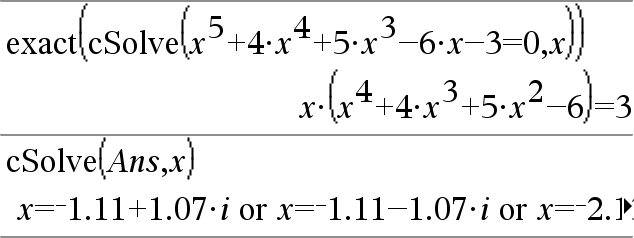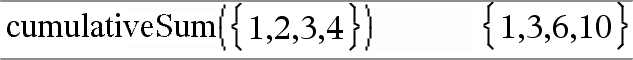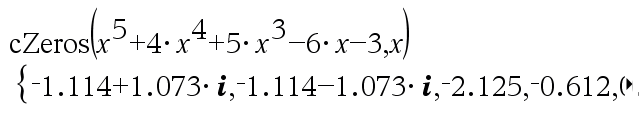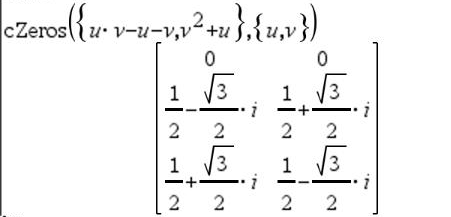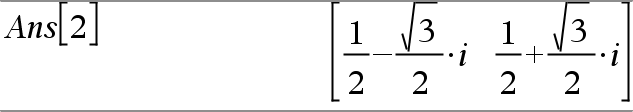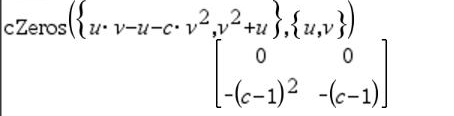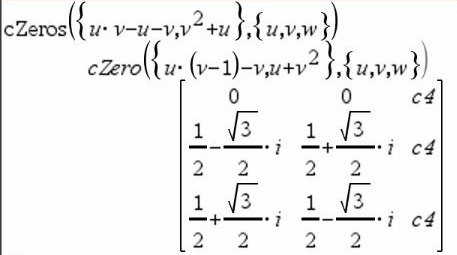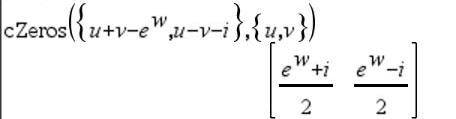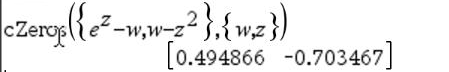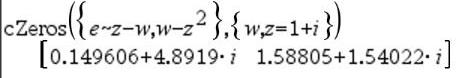|
Katalogi > |
|
|
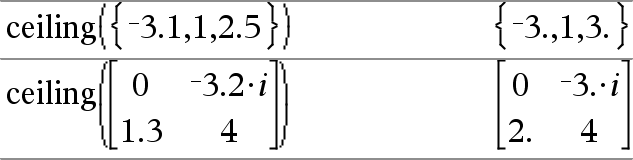
ceiling(Laus1)Þkokonaisluku Laskee lähimmän kokonaisluvun, joka on | argumentti. Argumentti voi olla reaali- tai kompleksiluku. Huomaa: Katso myös floor(). |
|
|
ceiling(Lista1)Þlista Laskee listan tai matriisin jokaisen elementin ylärajasta. |
|
|
Katalogi > |
|
|
Laskee numeerisen derivaatan käyttäen keskeiserotusosamäärän kaavaa. Kun Arvo määritetään, se ohittaa mahdolliset aikaisemmat muuttujamääritykset tai mahdolliset muuttujan nykyiset “|” -sijoitukset. Askel on askeleen arvo. Jos Askel jätetään pois, sen oletusarvo on 0.001. Lista1:tä tai Matriisi1:tä käytettäessä operaatio mapataan listan arvojen tai matriisin elementtien suhteen. Huomaa: Katso myös |
|
|
Katalogi > |
|
|
cFactor(Laus1[,Muutt])Þlauseke cFactor(Laus1) jakaa Laus1:n kaikki muuttujat supistaen ne yhteisellä nimittäjällä. Laus1:ä jaetaan tekijöihin mahdollisimman paljon kohti lineaarisia rationaalitekijöitä, vaikka tästä saataisiin uusia ei-reaalilukuja. Tämä vaihtoehto on sopiva, jos haluat jakaa lausekkeen tekijöihin useamman kuin yhden muuttujan suhteen. |
|
|
cFactor(Laus1,Muutt) jakaa Laus1:n tekijöihin muuttujan Muutt suhteen. Laus1:ä jaetaan tekijöihin mahdollisimman paljon kohti tekijöitä, jotka ovat lineaarisia muuttujassa Muutt, sisältäen mahdollisesti ei-reaalisia vakioita, vaikka tästä saataisiin irrationaalisia vakioita tai alalausekkeita, joissa on muita irrationaalisia muuttujia. Tekijät ja niiden termit lajitellaan siten, että Muutt on päämuuttuja. Muuttujan Muutt samanlaiset potenssit kerätään jokaisessa tekijässä. Muuttujan Muutt tulee olla mukana, jos vain kyseistä muuttujaa halutaan jakaa tekijöihin ja jos irrationaalilausekkeet ovat hyväksyttäviä kaikissa muissa muuttujissa, jotta muuttujaa Muutt voitaisiin jakaa enemmän tekijöihin. Toimenpiteessä voi esiintyä jonkin verran satunnaista muiden muuttujien tekijöihin jakamista. |
|
|
Auto or Approximate (Automaattinen tai likimääräinen) -tilan Auto (Automaattinen) -asetuksessa muuttujan Muutt mukanaolo sallii myös likiarvoistamisen liukulukuvakioilla, kun irrationaalisia kertoimia ei voida ilmaista täsmällisen tiiviisti sisäänrakennetuilla termeillä. Vaikka muuttujia olisi vain yksi, muuttujan Muutt mukanaolo voi tuottaa täydellisemmän tekijöihin jakamisen. Huomaa: Katso myös factor(). |
Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8. |
|
Katalogi > |
|
|
char(Kokonaisluku)Þmerkki Näyttää vastauksena merkkijonon, joka sisältää kämmenlaitteen merkkisarjasta olevan merkin, jonka tunnusnumero on Kokonaisluku. Kokonaisluvun Kokonaisluku sallittu alue on 0–65535. |
|
|
Katalogi > |
|
|
charPoly(neliömatriisi,Muutt)Þpolynomilauseke charPoly(neliömatriisi,Laus)Þpolynomilauseke charPoly(neliömatriisi1,Matriisi2)Þpolynomilauseke Laskee neliömatriisin karakteristisen polynomin. Lausekkeen n×n matriisi A karakteristinen polynomi, merkitään pA(l), on polynomi, joka on määritetty lausekkeella pA(l) = det(l• I NA) jossa I tarkoittaa identtistä matriisia n×n. neliömatriisi1:n ja neliömatriisi2:n on oltava samankokoiset. |
|
|
Katalogi > |
|
|
c22way ObsMatriisi chi22way ObsMatriisi Laskee c2-testin tarkasteltavan matriisin ObsMatriisi sisältämän kaksisuuntaisen lukemataulukon arvojen välisestä assosiaatiosta. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso täältä.) Lisätietoja matriisissa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla täältä. |
|
|
Tulosmuuttuja |
Kuvaus |
|
stat.c2 |
Khin neliö -tilasto: summa (tarkasteltava - odotettu)2/odotettu |
|
stat.PVal |
Alin merkitsevyystaso, jolla nollahypoteesi voidaan hylätä |
|
stat.df |
Khin neliö -tilastojen vapausasteet |
|
stat.ExpMat |
Odotetun elementtilukemataulukon matriisi, oletuksena nollahypoteesi |
|
stat.CompMat |
Elementtien Khin neliö -tilastokontribuutioiden matriisi |
|
Katalogi > |
|
|
c2Cdf(alaraja,yläraja,df)Þluku, jos alaraja ja yläraja ovat lukuja, lista, jos alaraja ja yläraja ovat listoja chi2Cdf(alaraja,yläraja,df)Þluku, jos alaraja ja yläraja ovat lukuja, lista, jos alaraja ja yläraja ovat listoja Laskee c2-jakauman todennäköisyyden alarajan ja ylärajan väliltä määritetylle vapausasteelle df. Kun P(X { yläraja), aseta alaraja= 0. Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla täältä. |
|
|
Katalogi > |
|
|
c2GOF obsLista,expLista,df chi2GOF obsLista,expLista,df Suorittaa testin, jolla varmistetaan, että otoksen data on tiettyä jakaumaa vastaavasta perusjoukosta. obsList on lukemalista, ja sen tulee sisältää kokonaislukuja. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso täältä.) Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla täältä. |
|
|
Tulosmuuttuja |
Kuvaus |
|
stat.c2 |
Khin neliö -tilasto: sum((tarkasteltava - odotettu)2/odotettu |
|
stat.PVal |
Alin merkitsevyystaso, jolla nollahypoteesi voidaan hylätä |
|
stat.df |
Khin neliö -tilastojen vapausasteet |
|
stat.CompList |
Elementtien Khin neliö -tilastokontribuutiot |
|
Katalogi > |
|
|
c2Pdf(XArvo,df)Þluku, jos XArvo on luku, lista, jos XArvo on lista chi2Pdf(XArvo,df)Þluku, jos XArvo on luku, lista, jos XArvo on lista Laskee c2-jakauman todennäköisyystiheysfunktion (pdf) määritetyllä XArvon arvolla määritetylle vapausasteelle df. Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla täältä. |
|
|
Katalogi > |
|
|
clearAZ Poistaa kaikki yksikirjaimiset muuttujat nykyiseltä tehtäväalueelta. Jos yksi tai useampia muuttujia on lukittu, tämä komento aiheuttaa virheilmoituksen ja poistaa vain lukitsemattomat muuttujat. Katso |
|
|
Katalogi > |
|
|
Poistaa virhetilan ja nollaa järjestelmän muuttujan errCode . Else-lauseessa lohkossa Try...Else...EndTry tulee käyttää komentoa ClrErr tai PassErr. Jos virhe on tarkoitus käsitellä tai jättää huomiotta, käytä komentoa ClrErr. Jos et tiedä, mitä tehdä virheen suhteen, lähetä se seuraavaan virheenkäsittelijään käyttämällä komentoa PassErr. Jos odottavia Try...Else...EndTry-virheenkäsittelijöitä ei ole enää, virheen valintaikkuna tulee näkyviin normaalisti. Huomaa: Katso myös PassErr, täältä, ja Try, täältä. Huomaa esimerkkiä syöttäessäsi: Ohjeet monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta. |
Esimerkki ClrErr-komennosta, katso esimerkki 2 Try-komennon kohdalla, täältä.
|
|
Katalogi > |
|
|
colAugment(Matriisi1, Matriisi2)Þmatriisi Luo uuden matriisin, joka on Matriisi2 liitettynä Matriisi1:een. Matriiseiden sarakemäärän on oltava sama, ja Matriisi2 liitetään Matriisi1:een uusina riveinä. Ei muuta Matriisi1:ä eikä Matriisi2:a. |
|
|
Katalogi > |
|
|
colDim(Matriisi)Þlauseke Laskee Matriisin sisältämien sarakkeiden lukumäärän. Huomaa: Katso myös rowDim(). |
|
|
Katalogi > |
|
|
colNorm(Matriisi)Þlauseke Laskee maksimiarvon Matriisin sarakkeissa olevien elementtien itseisarvojen summista. Huomaa: Määrittämättömät matriisielementit eivät ole sallittuja. Katso myös rowNorm(). |
|
|
Katalogi > |
|
|
comDenom(Laus1[,Muutt])Þlauseke comDenom(Laus1) supistaa täydellisesti lavennetun osoittajan täydellisesti lavennetulla nimittäjällä. |
|
|
comDenom(Laus1,Muutt) supistaa osoittajan ja nimittäjän, jotka on lavennettu muuttujalla Muutt. Termit ja niiden tekijät lajitellaan siten, että Muutt on päämuuttuja. Muuttujan Muutt samanlaiset potenssit kerätään. Toimenpiteessä voi esiintyä jonkin verran kerättyjen kertoimien satunnaista tekijöihin jakamista. Verrattuna siihen, että muuttuja Muutt jätettäisiin pois, tämä toiminto säästää usein aikaa, muistia ja näyttötilaa, ja samalla lausekkeesta tulee ymmärrettävämpi. Lisäksi tulokseen kohdistuvat seuraavat operaatiot ovat nopeampia eivätkä kuluta muistia yhtä todennäköisesti. |
|
|
Jos muuttujaa Muutt ei ole Laus1:ssä, comDenom(Laus1,Muutt) supistaa laventamattoman osoittajan laventamattomalla nimittäjällä. Tällaiset tulokset säästävät yleensä vielä enemmän aikaa, muistia ja näyttötilaa. Tällaiset osittain tekijöihin jaetut tulokset nopeuttavat myös seuraavia tulokseen kohdistuvia operaatioita eivätkä kuluta muistia läheskään yhtä todennäköisesti. |
|
|
Vaikka nimittäjää ei olisi, comden-funktio on usein nopea tapa suorittaa osittainen tekijöihin jako, mikäli factor() on liian hidas tai käyttää liikaa muistia. Vinkki: Syötä tämä comden()-funktion määritys ja kokeile sitä rutiininomaisesti vaihtoehtona funktioille comDenom() ja factor(). |
|
|
Katalogi > |
|
|
Muuntaa muotoa a·x2+b·x+c olevan toisen asteen polynomilausekkeen muotoon a·(x-h)2+k - tai - Muuntaa muotoa a·x2+b·x+c olevan toisen asteen yhtälön muotoon a·(x-h)2+k Ensimmäisen argumentin on oltava toisen asteen lauseke tai yhtälö vakiomuodossa toisen argumentin suhteen. Toisen argumentin on oltava yhden muuttujan termi tai yhden muuttujan termi korotettuna rationaaliseen potenssiin x, y2 tai z(1/3). Kolmas ja neljäs syntaksi yrittävät neliöksi täydentämisen muuttujien Var1, Var2 [,… ]) suhteen. |
|
|
Katalogi > |
|
|
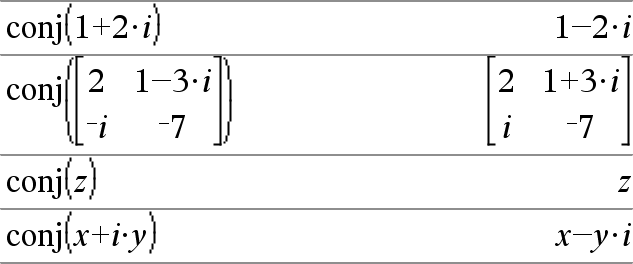
Laskee argumentin liittokompleksiluvun. Huomaa: Kaikkia määrittämättömiä muuttujia käsitellään reaalimuuttujina. |
|
|
Katalogi > |
|
|
constructMat(Laus,Muutt1,Muutt2,numRivit,numSarakkeet) Laskee matriisin argumentteihin perustuen. Laus on lauseke muuttujissa Muutt1 ja Muutt2. Tuloksena olevan matriisin elementit muodostetaan sieventämällä Laus jokaisella Muutt1:n ja Muutt2:n lisätyllä arvolla. Muutt1:ä lisätään automaattisesti välillä 1 - numRivit. Kullakin rivillä Muutt2:a lisätään välillä 1 - numSarakkeet. |
|
|
Katalogi > |
|
|
CopyVar Muutt1, Muutt2 CopyVar Muutt1., Muutt2. CopyVar Muutt1, Muutt2 kopioi muuttujan Muutt1 arvon muuttujaan Muutt2 ja luo tarvittaessa Muutt2:n. Muuttujalla Muutt1 on oltava arvo. Jos Muutt1 on olemassa olevan käyttäjän määrittämän funktion nimi, kopioi kyseisen funktion määrityksen funktioon Muutt2. Funktio Muutt1 on määritettävä. Muutt1:n on oltava muuttujien nimeämissääntöjen mukainen tai epäsuora lauseke, joka sieventyy näitä vaatimuksia vastaavaksi muuttujan nimeksi. |
|
|
CopyVar Muutt1., Muutt2. kopioi kaikki Muutt1:n jäsenet. muuttujaryhmä Var2:een. ryhmä, Muutt2:n luominen. tarvittaessa. Muutt1. tulee olla olemassa olevan muuttujaryhmän nimi, kuten tilastollinen stat.nn vastausta tai muuttujaa, jotka on luotu funktiolla |
|
|
Katalogi > |
|
|
corrMat(Lista1,Lista2[,…[,Lista20]]) Laskee korrelaatiomatriisin laajennetulle matriisille [Lista1, Lista2, ..., Lista20]. |
|
|
Katalogi > |
|
|
Laus ►cos Huomaa: Voit syöttää tämän operaattorin tietokoneen näppäimistöltä kirjoittamalla @>cos. Näyttää Laus:n kulman kosinin. Tämä on näytön muunnosoperaattori. Sitä voidaan käyttää vain syöterivin lopussa. ►cos alentaa kaikkia lausekkeen Huomaa: Tätä muunnosoperaattoria ei tueta aste- eikä graadikulmatilassa. Ennen kuin käytät sitä, varmista, että kulmatila on asetettu radiaaneiksi ja että Laus ei sisällä eksplisiittisiä viittauksia aste- tai graadikulmiin. |
|
|
µ painike |
|
|
cos(Lista1) määrittää listan kaikkien Lista1:n sisältämien elementtien kosineista. Huomaa: Argumentti tulkitaan aste-, graadi- tai radiaanikulmaksi käytössä olevan kulmatila-asetuksen mukaisesti. Voit ohittaa kulmatilan väliaikaisesti painikkeilla ¡, G tai R. |
Astekulmatilassa:
Radiaanikulmatilassa:
|
|
cos(neliömatriisi1)Þneliömatriisi Laskee neliömatriisi1:n matriisikosinin. Tämä ei ole sama kuin kunkin elementin kosinin laskeminen. Kun skaalarista funktiota f(A) käytetään neliömatriisi1:een (A), tulos lasketaan algoritmilla: Laske A:n ominaisarvot (li) ja ominaisvektorit (Vi). neliömatriisi1:n on oltava diagonalisoitavissa. Lisäksi siinä ei voi olla symbolisia muuttujia, joille ei ole määritetty arvoa. Matriiseista: Tällöin A = X B X/ja f(A) = X f(B) X/. Esimerkiksi, cos(A) = X cos(B) X/, jossa: cos(B) =
Kaikki laskut suoritetaan liukulukuaritmetiikalla. |
Radiaanikulmatilassa:
|
|
µ painike |
|
|
cos/(Laus1)Þlauseke cos/(Lista1)Þlista
cos/(Lista1) laskee listan Lista1:n jokaisen elementin käänteiskosineista. Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana käytössä olevan kulmatila-asetuksen mukaisesti. Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla arccos(...). |
Astekulmatilassa:
|
|
cos/(neliömatriisi1)Þneliömatriisi Laskee neliömatriisi1:n matriisin käänteiskosinin. Tämä ei ole sama kuin kunkin elementin käänteiskosinin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos(). neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja. |
Radiaanikulmatilassa ja suorakulmakompleksimuodossa:
Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8. |
|
Katalogi > |
|
|
cosh(Lista1) määrittää listan Lista1:n kunkin elementin hyperbolisista kosineista. |
Astekulmatilassa:
|
|
cosh(neliömatriisi1)Þneliömatriisi Laskee neliömatriisi1:n matriisin hyperbolisen kosinin. Tämä ei ole sama kuin kunkin elementin hyperbolisen kosinin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos(). neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja. |
Radiaanikulmatilassa: |
|
Katalogi > |
|
|
cosh/(Laus1)Þlauseke cosh/(Lista1)Þlista
cosh/(Lista1) määrittää listan Lista1:n kunkin elementin käänteisistä hyperbolisista kosineista. Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla arccosh(...). |
|
|
cosh/(neliömatriisi1)Þneliömatriisi Laskee neliömatriisi1:n matriisin käänteisen hyperbolisen kosinin. Tämä ei ole sama kuin kunkin elementin käänteisen hyperbolisen kosinin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos(). neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja. |
Radiaanikulmatilassa ja suorakulmakompleksimuodossa: Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8. |
|
µ painike |
|
|
Laskee Laus1:n kotangentin tai määrittää listan Lista1:n kaikkien elementtien kotangenteista. Huomaa: Argumentti tulkitaan aste-, graadi- tai radiaanikulmaksi käytössä olevan kulmatila-asetuksen mukaisesti. Voit ohittaa kulmatilan väliaikaisesti painikkeilla ¡, G tai R. |
Astekulmatilassa:
|
|
µ painike |
|
|
cot/(Laus1)Þlauseke cot/(Lista1)Þlista Laskee kulman, jonka kotangentti on Laus1, tai määrittää listan, joka sisältää Lista1:n kunkin elementin käänteiskotangentit. Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana käytössä olevan kulmatila-asetuksen mukaisesti. Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla arccot(...). |
Astekulmatilassa:
|
|
Katalogi > |
|
|
Laskee Laus1:n hyperbolisen kotangentin tai määrittää listan Lista1:n kaikkien elementtien hyperbolisista kotangenteista. |
|
|
Katalogi > |
|
|
coth/(Laus1)Þlauseke coth/(Lista1)Þlista Laskee Laus1:n käänteisen hyperbolisen kotangentin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien käänteiset hyperboliset kotangentit. Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla arccoth(...). |
|
|
Katalogi > |
|
|
count(Arvo1taiLista1 [,Arvo2taiLista2 [,...]])Þarvo Laskee elementtien kokonaismäärän argumenteille, jotka sieventyvät numeroarvoiksi. Argumentit voivat olla lausekkeita, arvoja, listoja tai matriiseja. Argumenttien datatyypit voivat olla erilaisia, ja argumentit voivat olla erikokoisia. Listan, matriisin tai solualueen jokainen elementti sievennetään, jotta voidaan määrittää, kuuluuko se laskettavaan lukumäärään. Listat & Taulukot -sovelluksessa voit käyttää solualueita argumenttien tilalla. Tyhjiä elementtejä ei huomioida. Lisätietoja tyhjistä elementeistä, katso täältä. |
Viimeisessä esimerkissä lukumäärään lasketaan mukaan vain 1/2 ja 3+4*i. Muut argumenteista, olettaen että x on määrittämätön, eivät sievenny numeroarvoiksi. |
|
Katalogi > |
|||||||
|
countif(Lista,Kriteerit)Þarvo Laskee niiden Listan sisältämien elementtien kokonaismäärän, jotka vastaavat määritettyjä kriteereitä Kriteerit. Kriteeri voi olla:
Listat & Taulukot -sovelluksessa voit käyttää solualueita Listan tilalla. Listassa olevia tyhjiä elementtejä ei huomioida. Lisätietoja tyhjistä elementeistä, katso täältä. |
Laskee niiden elementtien lukumäärän, jotka ovat yhtä kuin 3.
Laskee niiden elementtien lukumäärän, jotka ovat yhtä kuin "def".
Laskee niiden elementtien lukumäärän, jotka ovat yhtä kuin x; tässä esimerkissä oletetaan, että muuttuja x on määrittämätön.
Laskee lukumäärään 1:n ja 3:n.
Laskee lukumäärään 3:n, 5:n ja 7:n.
Laskee lukumäärään 1:n, 3:n, 7:n ja 9:n. |
|
Katalogi > |
|
|
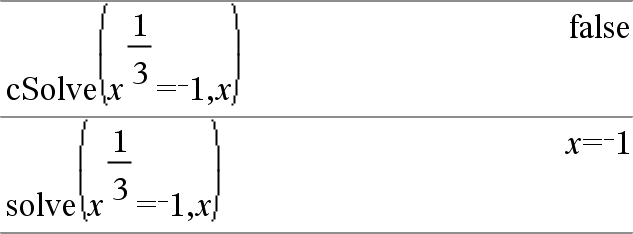
Ensimmäinen syntaksi,
Toinen syntaksi, Huomaa: Katso myös |
|
|
Katalogi > |
|
|
crossP(Lista1, Lista2)Þlista Määrittää listan Lista1:n ja Lista2:n ristitulosta. Lista1:n ja Lista2:n on oltava samankokoiset, ja koon on oltava joko 2 tai 3. |
|
|
crossP(Vektori1, Vektori2)Þvektori Laskee rivi- tai sarakevektorin (argumenteista riippuen), joka on Vektori1:n ja Vektori2:n ristitulo. Sekä Vektori1:n että Vektori2:n on oltava rivivektoreita tai sarakevektoreita. Vektoreiden on oltava samankokoiset, ja koon tulee olla joko 2 tai 3. |
|
|
µ painike |
|
|
Laskee Laus1:n kosekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien kosekantit. |
Astekulmatilassa:
|
|
µ painike |
|
|
csc/(Laus1) Þ lauseke csc/(Lista1) Þ lista Laskee kulman, jonka kosekantti on Laus1, tai määrittää listan, joka sisältää Lista1:n kunkin elementin käänteiskosekantit. Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana käytössä olevan kulmatila-asetuksen mukaisesti. Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla arccsc(...). |
Astekulmatilassa:
|
|
Katalogi > |
|
|
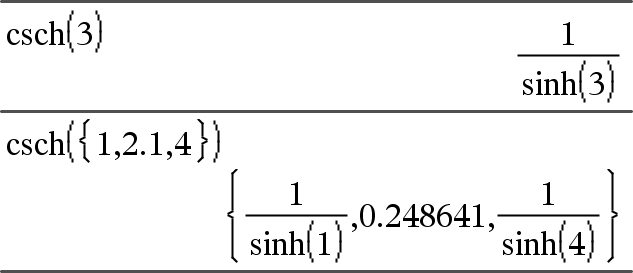
csch(Laus1) Þ lauseke csch(Lista1) Þ lista Laskee Laus1:n hyperbolisen kosekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien hyperboliset kosekantit. |
|
|
Katalogi > |
|
|
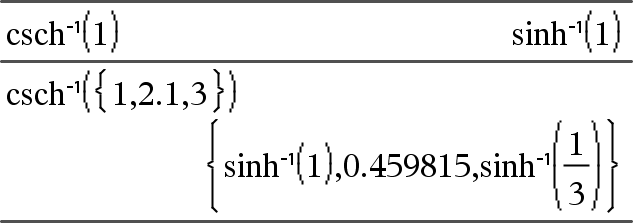
csch/(Laus1) Þ lauseke csch/(Lista1) Þ lista
Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla arccsch(...). |
|
|
Katalogi > |
|
|
CubicReg X, Y[, [Frekv] [, Luokka, Sisällytä]] Laskee 3. asteen polynomiregressiony = a·x3+b· x2+c·x+dlistoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso täältä.) Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta. X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja | 0. Luokka on luokkakoodien lista vastaavalle X- ja Y -datalle. Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa. Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla täältä. |
|
|
Tulosmuuttuja |
Kuvaus |
|
stat.RegEqn |
Regressioyhtälö: a·x3+b·x2+c·x+d. |
|
stat.a, stat.b, stat.c, stat.d |
Regressiokertoimet. |
|
stat.R2 |
Määrityskerroin. |
|
stat.Resid |
Regressioyhtälön jäännökset |
|
stat.XReg |
Muokatun X Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv, Luokkalista ja Sisällytä luokat rajoitusten mukaisesti. |
|
stat.YReg |
Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv, Luokkalista ja Sisällytä luokat rajoitusten mukaisesti. |
|
stat.FreqReg |
Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista. |
|
Katalogi > |
|
|
cumulativeSum(Lista1)Þlista Laskee listan Lista1:n sisältämien elementtien kumulatiivisista summista alkaen elementistä 1. |
|
|
cumulativeSum(Matriisi1)Þmatriisi Laskee matriisin Matriisi1:n sisältämien elementtien kumulatiivisista summista. Jokainen elementti on ylhäältä alas ulottuvan sarakkeen kumulatiivinen summa. Tyhjä elementti listassa Lista1 tai matriisissa Matriisi1 tuottaa tyhjän elementin tuloksena olevaan listaan tai matriisiin. Lisätietoja tyhjistä elementeistä, katso täältä. |
|
|
Katalogi > |
|
|
Cycle Siirtää ohjauksen välittömästi nykyisen silmukan (For, While tai Loop) seuraavaan iteraatioon. Cycle ei ole sallittu näiden kolmen silmukkarakenteen (For, While tai Loop) ulkopuolella. Huomaa esimerkkiä syöttäessäsi: Ohjeet monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta. |
Funktio, joka laskee yhteen kokonaisluvut väliltä 1-100 ohittaen luvun 50.
|
|
Katalogi > |
|
|
Vektori 4Cylind Huomaa: Voit syöttää tämän operaattorin tietokoneen näppäimistöltä kirjoittamalla @>Cylind. Näyttää rivi- tai sarakevektorin sylinterin muodossa [r,±q, z]. Vektorissa on oltava täsmälleen kolme elementtiä. Se voi olla joko rivi tai sarake. |
|