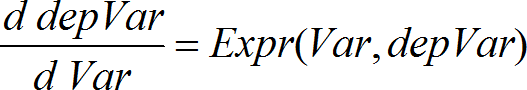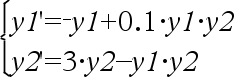|
u painike |
|
|
Laskee e:n arvon korotettuna Arvo1:n potenssiin. Huomaa: Katso myös e eksponenttimalli, täältä. Huomaa: Painikkeen u painaminen, jotta näkyviin saadaan e^(, on eri asia kuin näppäimistön merkin E painaminen. Voit syöttää kompleksiluvun rei q polaarisessa muodossa. Käytä tätä muotoa kuitenkin vain radiaanikulmatilassa; aste- tai graadikulmatilassa se aiheuttaa määritysjoukkovirheen (Domain). |
|
|
e^(Lista1)Þlista Laskee e:n arvon korotettuna Lista1:n jokaisen elementin potenssiin. |
|
|
e^(neliömatriisi1)Þneliömatriisi Laskee neliömatriisi1:n matriisieksponentin. Tämä ei ole sama kuin laskettaessa e korotettuna kunkin elementin mukaiseen potenssiin. Laskentamenetelmä on kuvattu kohdassa cos(). neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja. |
|
|
Katalogi > |
|
|
eff(nimelliskorko,CpY)Þarvo Talouslaskentatoiminto, joka muuntaa nimelliskorkokannan nimelliskorko efektiiviseksi vuosikoroksi, kun CpY määritetään korkojaksojen lukumääräksi vuodessa. nimelliskoron on oltava reaaliluku, ja CpY:n on oltava reaaliluku > 0. Huomaa: Katso myös nom(), täältä. |
|
|
Katalogi > |
|
|
eigVc(neliömatriisi)Þmatriisi Laskee matriisin, joka sisältää ominaisvektorit reaaliselle tai kompleksiselle neliömatriisille, jossa jokainen vastauksen sarake vastaa ominaisarvoa. Huomaa, että ominaisvektori ei ole yksilöllinen; sitä voidaan skaalata millä tahansa vakiokertoimella. Ominaisvektorit ovat normaalimuotoisia, mikä tarkoittaa, että, jos V = [x1, x2, … , xn], tällöin: x12 + x22 + … + xn2 = 1 neliömatriisia tasapainotetaan ensin similaarimuunnoksilla, kunnes rivi- ja sarakenormit ovat mahdollisimman lähellä samaa arvoa. Sen jälkeen neliömatriisi sievennetään Hessenbergin ylämatriisimuotoon ja ominaisvektorit lasketaan Schurin tekijöihin jaon menetelmällä. |
Suorakulmakompleksimuodossa:
Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8. |
|
Katalogi > |
|
|
eigVl(neliömatriisi)Þlista Laskee listan reaalisen tai kompleksisen neliömatriisin ominaisarvoista. neliömatriisia tasapainotetaan ensin similaarimuunnoksilla, kunnes rivi- ja sarakenormit ovat mahdollisimman lähellä samaa arvoa. Sen jälkeen neliömatriisi sievennetään Hessenbergin ylämatriisimuotoon ja ominaisarvot lasketaan Hessenbergin ylämatriisista. |
Suorakulmakompleksimuodossa:
Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8. |
|
Katso If, täältä. |
|
|
|
|
|
Katalogi > |
|
|
If BoolenLaus1 Then Huomaa esimerkkiä syöttäessäsi: Ohjeet monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta. |
|
|
EndFor |
Katso For, täältä. |
|
|
|
|
Katso Func, täältä. |
|
|
|
|
|
Katso If, täältä. |
|
|
|
|
|
Katso Loop, täältä. |
|
|
|
|
|
EndPrgm |
Katso Prgm, täältä. |
|
|
|
|
EndTry |
Katso Try, täältä. |
|
|
|
|
Katso While, täältä. |
|
|
|
|
|
Katalogi > |
|
|
Käyttää Eulerin menetelmää järjestelmän ratkaisuun
muuttujalla depVar(Var0)=depVar0 välillä [Var0,VarMax]. Laskee matriisin, jonka ensimmäinen rivi määrittelee Var tulosarvot ja jonka toinen rivi määrittelee ensimmäisen ratkaisukomponentin arvon vastaavilla Var-arvoilla jne. Expr on oikea puoli, joka määrittelee tavallisen differentiaaliyhtälön (ODE). SystemOfExpr on oikeiden puolten ryhmä, joka määrittelee ODE-yhtälöiden ryhmän (vastaa riippuvien muuttujien järjestystä kohdassa ListOfDepVars). ListOfExpr on oikeiden puolten luettelo, joka määrittelee ODE-yhtälöiden ryhmän (vastaa riippuvien muuttujien järjestystä kohdassa ListOfDepVars). Var on riippumaton muuttuja. ListOfDepVars on riippuvien muuttujien luettelo. {Var0, VarMax} on kahden elementin lista, joka määrittää funktion integroinnin muuttujasta Var0 muuttujaan VarMax. ListOfDepVars0 on riippuvien muuttujien alkuehtojen luettelo. VarStep nollasta eroava numero niin, että eulerStep on positiivinen kokonaisluku (oletus 1), joka määrittelee Eulerin vaiheiden määrän tulosarvojen välillä. Eulerin menetelmän käyttämä varsinainen vaihemäärä on VarStepàeulerStep. |
Differentiaaliyhtälö: Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8.
Yhtälöryhmä: |
|
Laitevalikko |
|
|
eval() on validi vain TI-Innovator™ Hub ohjelmointikomentojen komentoargumenteissa Get, GetStr, ja Send. Ohjelmisto käsittelee lausekkeen Expr ja korvaa eval()-ilmauksen lopputuloksella merkkijoukkona Argumentin Expr on sievennyttävä reaaliluvuksi. |
Aseta RGB-ledin sininen väri puolelle intensiteetille.
Palauta sininen väri OFF-tilaan.
eval()-argumentin on sievennyttävä reaaliluvuksi.
Ohjelmoi punainen väri voimistumaan
Suorita ohjelma.
|
|
Vaikka eval() ei näytä tulostaan,voi tuloksena saatavaa laitekomentojonoa katsoa komennon suorittamisen jälkeen tarkastamalla jonkin seuraavista erikoismuuttujista. iostr.SendAns Huomio: Katso myös Get (täältä), GetStr (täältä), ja Send (täältä). |
|
|
Katalogi > |
|
|
Exit Poistuu nykyisestä For-, While- tai Loop-lohkosta. Exit-komento ei ole sallittu näiden kolmen silmukkarakenteen (For, While tai Loop) ulkopuolella. Huomaa esimerkkiä syöttäessäsi: Ohjeet monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta. |
Funktion listaus:
|
|
u painike |
|
|
exp(Arvo1)Þarvo Laskee e:n arvon korotettuna Arvo1:n potenssiin. Huomaa: Katso myös e eksponenttimalli, täältä. Voit syöttää kompleksiluvun rei q polaarisessa muodossa. Käytä tätä muotoa kuitenkin vain radiaanikulmatilassa; aste- tai graadikulmatilassa se aiheuttaa määritysjoukkovirheen (Domain). |
|
|
exp(Lista1)Þlista Laskee e:n arvon korotettuna Lista1:n jokaisen elementin potenssiin. |
|
|
exp(neliömatriisi1)Þneliömatriisi Laskee neliömatriisi1:n matriisieksponentin. Tämä ei ole sama kuin laskettaessa e korotettuna kunkin elementin mukaiseen potenssiin. Laskentamenetelmä on kuvattu kohdassa cos(). neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja. |
|
|
Katalogi > |
|
|
expr(Merkkijono)Þlauseke Määrittää Merkkijonon sisältämän merkkijonon lausekkeena ja suorittaa toimenpiteen välittömästi. |
|
|
Katalogi > |
|
|
ExpReg X, Y [, [Frekv][, Luokka, Sisällytä]] Laskee eksponentiaalisen regressiony = a·(b)xlistoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso täältä.) Kaikkien listojen on oltava samankokoisia Sisällytä-listaa lukuunottamatta. X ja Y ovat riippumattomien ja riippuvien muuttujien listoja. Frekv on valinnainen frekvenssiarvojen lista. Jokainen Frekv:n elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja | 0. Luokka on Sisällytä on yhden tai usemman luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa. Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla täältä. |
|
|
Tulosmuuttuja |
Kuvaus |
|
stat.RegEqn |
Regressioyhtälö: a·(b)x |
|
stat.a, stat.b |
Regressiokertoimet |
|
stat.r2 |
Muunnettujen tietojen lineaarimäärittelyn kerroin |
|
stat.r |
Muunnettujen tietojen korrelaatiokerroin (x, ln(y)) |
|
stat.Resid |
Eksponentiaalimalliin liittyvät jäännökset |
|
stat.ResidTrans |
Muunnettujen tietojen lineaariseen sovitukseen liittyvät jäännökset |
|
stat.XReg |
Muokatun X Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv, Luokkalista ja Sisällytä luokat rajoitusten mukaisesti |
|
stat.YReg |
Muokatun Y Lista:n sisältämä datapisteiden lista, jota käytetään regressiossa komentojen Frekv, Luokkalista ja Sisällytä luokat rajoitusten mukaisesti |
|
stat.FreqReg |
Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista |