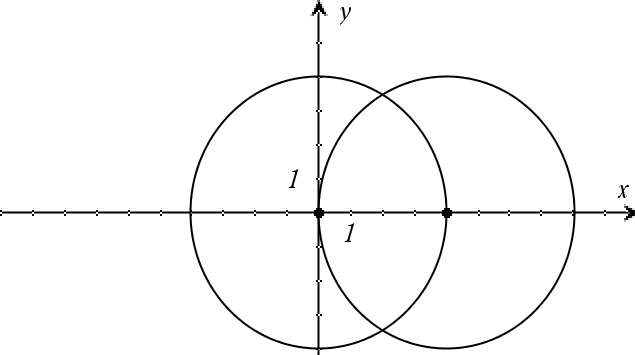
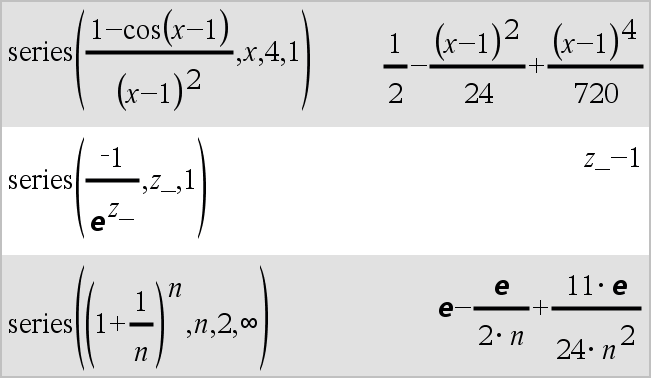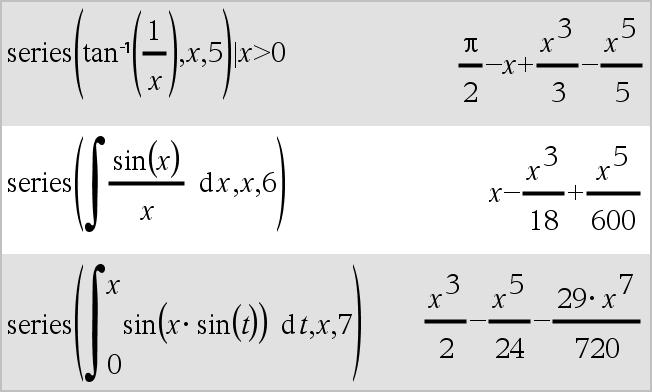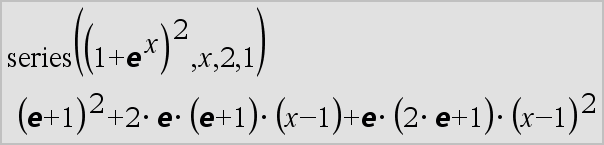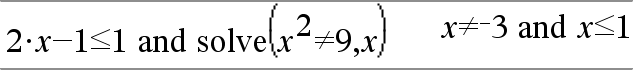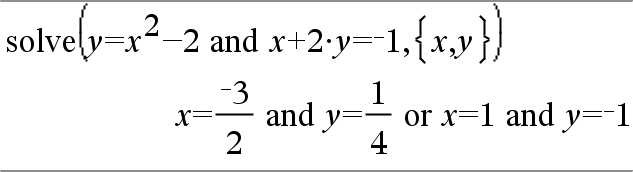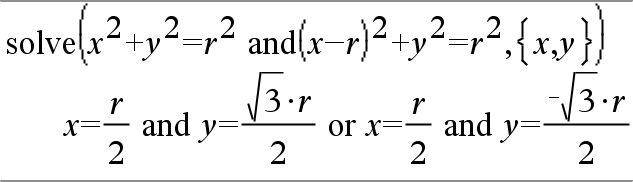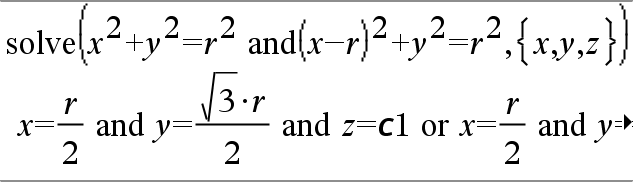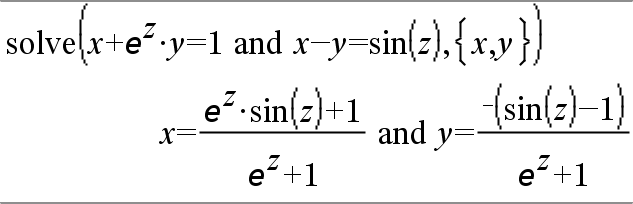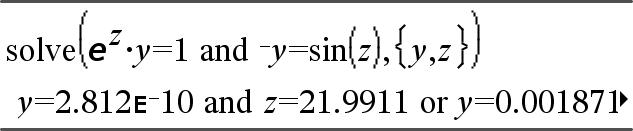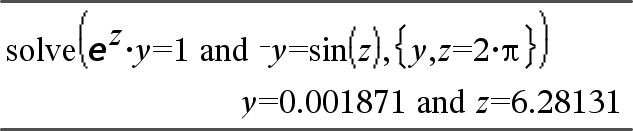|
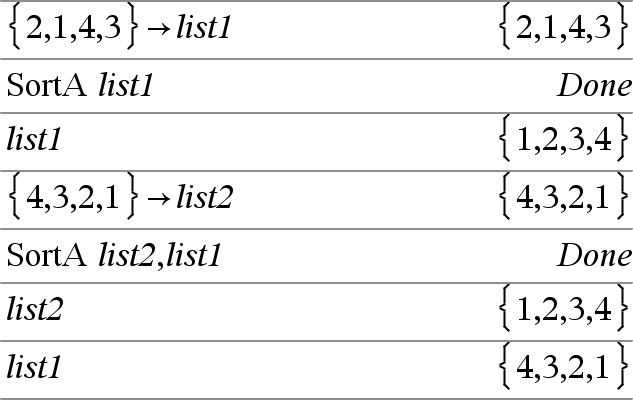
series(Expr1, Var, Order [, Point])ÞAusdruck
series(Expr1, Var, Order [, Point]) | Var>PointÞAusdruck
series(Expr1, Var, Order [, Point]) | Var<PointÞAusdruck
Gibt eine verallgemeinerte endliche Potenzreihe von Expr1 entwickelt um Point bis Grad Order zurück. Order kann jede beliebige rationale Zahl sein. Die resultierenden Potenzen von (Var N Point) können negative und/oder Bruchexponenten beinhalten. Die Koeffizienten dieser Potenzen können Logarithmen von (Var N Point) und andere Funktionen von Var beinhalten, die von allen Potenzen von (Var N Point) mit demselben Exponentenzeichen dominiert werden.
Point ist vorgegeben als 0. Point kann ˆ oder Nˆ sein; in diesen Fällen ist die Entwicklung durch Grad Order in 1/(Var N Point).
series(...) gibt “series(...)” zurück, wenn sie keine Darstellung bestimmen kann wie für wesentliche Singularitäten wie z.B. sin(1/z) bei z=0, eN1/z bei z=0 oder ez bei z = ˆ oder Nˆ.
Wenn die Reihe oder eine ihrer Ableitungen eine Sprungstelle bei Point hat, enthält das Ergebnis wahrscheinlich Unterausdrücke der Form sign(…) oder abs(…) für eine reelle Expansionsvariable oder (-1)floor(…angle(…)…) für eine komplexe Expansionsvariable, die mit “_” endet. Wenn Sie die Folge nur für Werte auf einer Seite von Point verwenden möchten, hängen Sie je nach Bedarf “| Var > Point”, “| Var < Point”, “| “Var | Point” oder “Var { Point” an, um ein einfacheres Ergebnis zu erhalten.
series() kann symbolische Approximationen für unbestimmte Integrale und bestimmte Integrale bereitstellen, für die anders keine symbolischen Lösungen erreicht werden können.
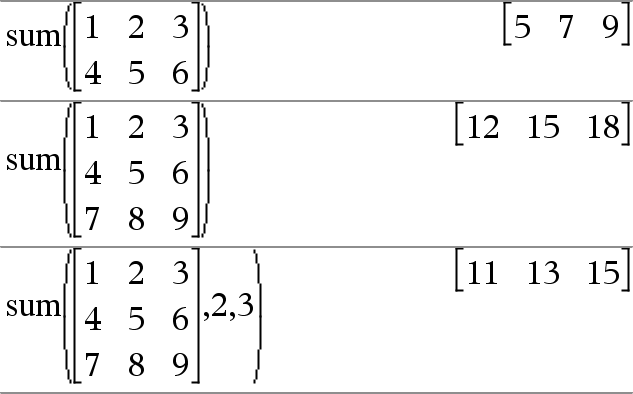
series() wird über Listen und Matrizen mit erstem Argument verteilt.
series() ist eine verallgemeinerte Version von taylor().
Wie im letzten nebenstehenden Beispiel demonstriert, können die Anzeigeroutinen hinter dem von series(...) erzeugten Ergebnis Terme so umstellen, dass der dominante Term nicht ganz links steht.
Hinweis: Siehe auch dominantTerm(), hier.
|
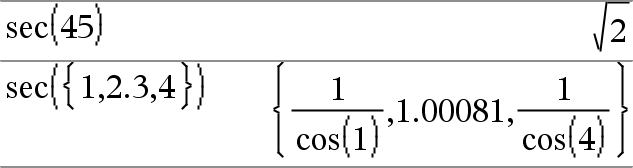




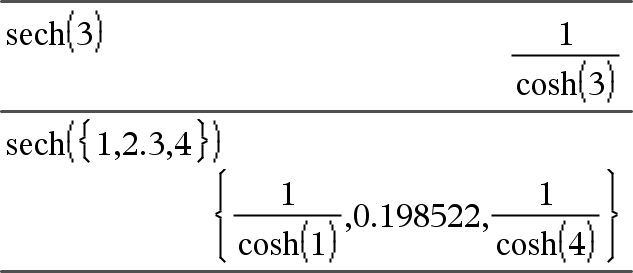
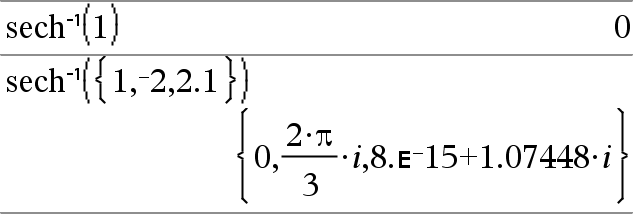



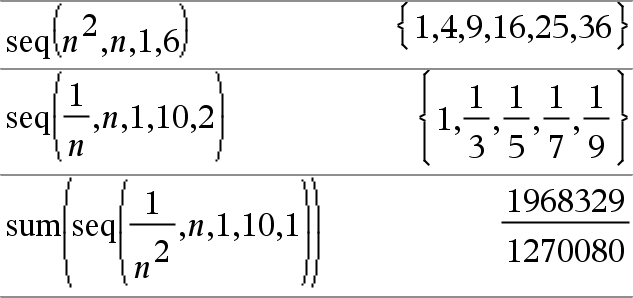
 aus.
aus.