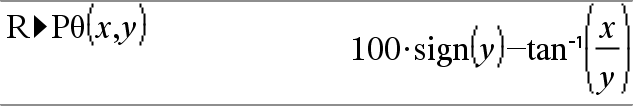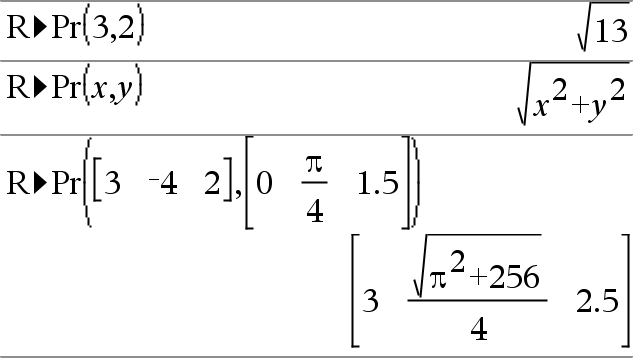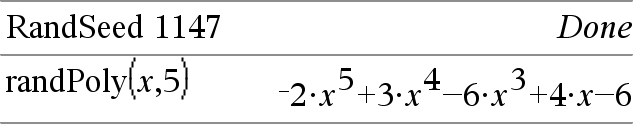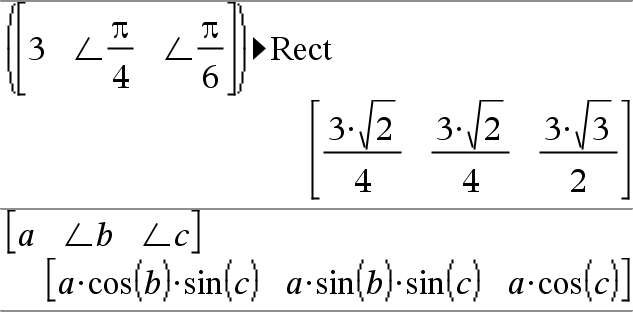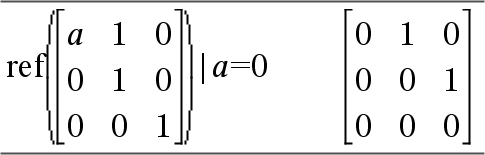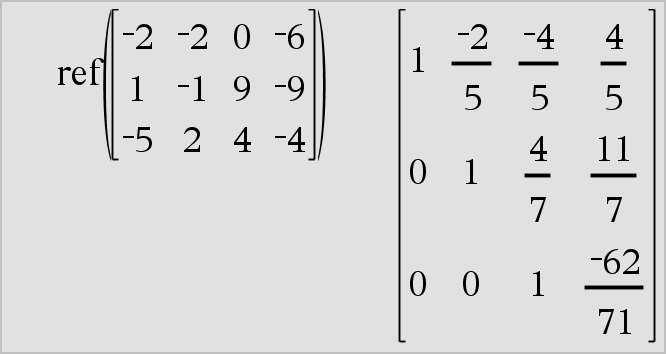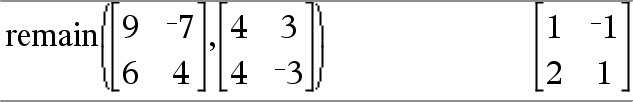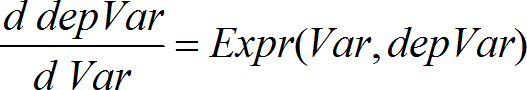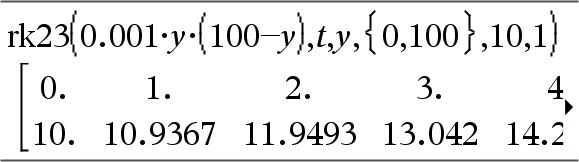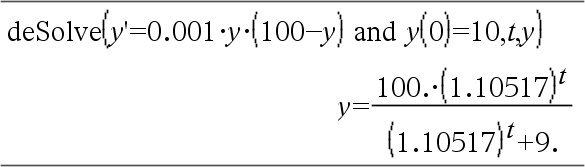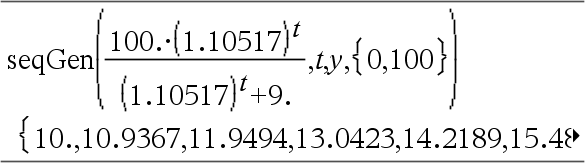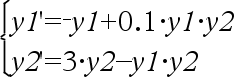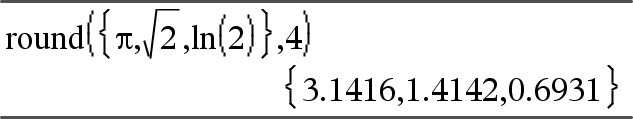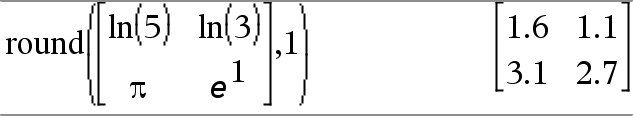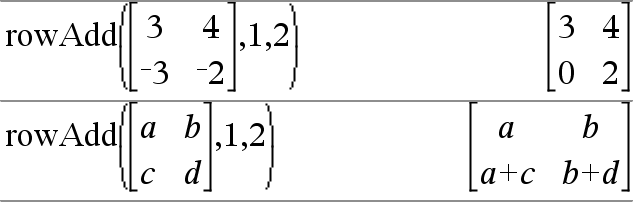|
Catálogo > |
|
|
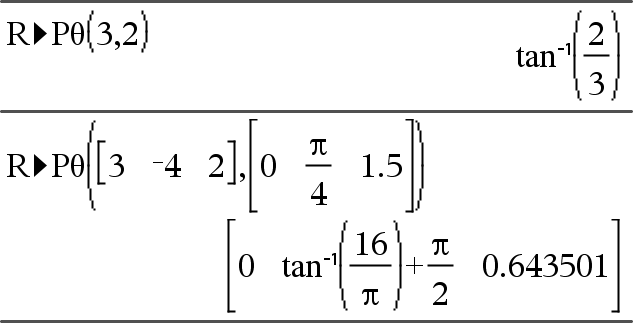
Devolve a coordenada θ equivalente dos Nota: O resultado é devolvido como um ângulo expresso em graus, grados ou radianos, de acordo com a definição do modo de ângulo atual. Nota: Pode introduzir esta função através da escrita de R@Ptheta(...) no teclado do computador |
No modo de ângulo de grau:
|
|
Catálogo > |
|
|
Devolve a coordenada r equivalente dos argumentos dos pares (x,y). Nota: Pode introduzir esta função através da escrita de R@Pr(...) no teclado do computador |
No modo de ângulo de Radianos:
|
|
Catálogo > |
|
|
Converte o argumento para a medição do ângulo de radianos. Nota: Pode introduzir esta função através da escrita de @Rad no teclado do computador |
No modo de ângulo de grau:
|
|
Catálogo > |
|
|
rand() ⇒ expressão rand() devolve um valor aleatório entre 0 e 1. rand(#Tentativas) devolve uma lista com # valores aleatórios entre 0 e 1 |
Define a semente do número aleatório.
|
|
Catálogo > |
|
|
randBin(n, p) ⇒ expressão randBin(n, p) devolve um número real aleatório de uma distribuição binomial especificada. randBin(n, p, #Tentativas) devolve uma lista com números reais aleatórios #Tentativas de uma distribuição binomial especificada. |
|
|
Catálogo > |
|
|
randInt(lowBound,upBound) ⇒ expressão randInt(LimiteInferior,LimiteSuperior) devolve um número inteiro aleatório no intervalo especificado pelos limites dos números inteiros LimiteInferior e LimiteSuperior. randInt(LimiteInferior,LimiteSuperior ,#Tentativas) devolve uma lista com # números inteiros aleatórios no intervalo especificado. |
|
|
Catálogo > |
|
|
randMat(LinhasNum, ColunasNum) ⇒ matriz Devolve uma matriz de números inteiros entre -9 e 9 da dimensão especificada. Ambos os argumentos têm de ser simplificados para números inteiros. |
Nota: Os valores desta matriz mudam sempre que prime . |
|
Catálogo > |
|
|
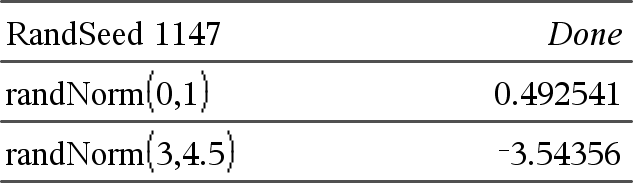
randNorm(μ, σ) ⇒ expressão randNorm(μ, σ) devolve um número decimal da distribuição normal específica. Pode ser qualquer número real, mas estará fortemente concentrado no intervalo [μ−3•σ, μ+3•σ]. randNorm(μ, σ, #Tentativas) devolve uma lista com números decimais #Tentativas de uma distribuição normal especificada. |
|
|
Catálogo > |
|
|
randPol y (Var, Ordem) ⇒ expressão Devolve um polinómio em Var da Ordem especificada. Os coeficientes são números inteiros aleatórios no intervalo −9 a 9. O coeficiente à esquerda não será zero. Ordem tem de ser 0–99. |
|
|
Catálogo > |
|
|
randSamp(Lista,#Tentativas[,SemSubstituição]) ⇒ lista Devolve uma lista com uma amostra aleatória de tentativas #Tentativas de Lista com uma opção para substituição da amostra (SemSubstituição=0) ou sem substituição da amostra (SemSubstituição=1). A predefinição é com substituição da amostra. |
|
|
Catálogo > |
|
|
RandSeed Número Se Número = 0, define as sementes para as predefinições de fábrica para o gerador de números aleatórios. Se Número ≠ 0, é utilizado para gerar duas sementes, que são guardadas nas variáveis do sistema seed1 e seed2. |
|
|
Catálogo > |
|
|
real(Expr1) ⇒ expressão Devolve a parte real do argumento.
|
|
|
real(Lista1) ⇒ lista Devolve as partes reais de todos os elementos. |
|
|
real(Matriz1) ⇒ matriz Devolve as partes reais de todos os elementos. |
|
|
Catálogo > |
|
|
Vetor ►Rect Nota: Pode introduzir este operador através da escrita de @Rect no teclado do computador. Apresenta o Vetor na forma retangular [x, y, z] O vetor tem de ser de dimensão 2 ou 3 e pode ser uma linha ou uma coluna. Nota: ►Rect é uma instrução de formato de visualização, não uma função de conversão. Só pode utilizá-la no fim de uma linha de entrada e não actualiza ans. Nota: Consulte também ►Polar, aqui. |
|
|
ValorComplexo ►Rect Apresenta o ValorComplexo na forma retangular a+bi. O ValorComplexo pode ter qualquer forma complexa. No entanto, uma entrada reiθ provoca um erro no modo de ângulo Graus. Nota: Tem de utilizar os parêntesis para uma entrada em coordenadas polares (r∠θ). |
No modo de ângulo de Radianos:
Nota: Para escrever ∠, selecione-o na lista de símbolos no Catálogo. |
|
Catálogo > |
|||||||
|
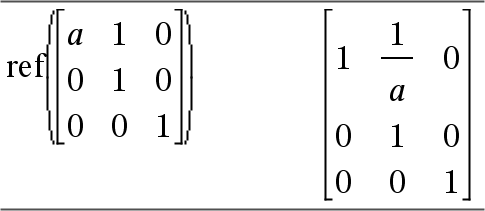
ref(Matriz1[, Tol]) ⇒ matriz Devolve a forma de escalão-linha de Matriz1. Opcionalmente, qualquer elemento da matriz é tratado como zero se o valor absoluto for inferior a Tol. Esta tolerância é utilizada apenas se a matriz tiver entradas de ponto flutuante e não contiver nenhuma variável simbólica sem nenhum valor atribuído. Caso contrário, Tol é ignorado.
Evite elementos indefinidos em Matriz1. Podem originar resultados inesperados. Por exemplo, se a for indefinido na expressão seguinte, aparece uma mensagem de aviso e o resultado é mostrado como:
O aviso aparece porque o elemento generalizado 1/a não seria válido para a=0. Pode evitar isto guardando um valor para a anteriormente ou utilizando o operador de limite (“|”) para substituir um valor, conforme indicado no exemplo seguinte.
Nota: Consulte também rref(), aqui. |
|
|
Catálogo > |
|||||||||||
|
AtualizarVarsSonda Permite-lhe aceder a dados de sensor a partir de todas as sondas de sensor ligadas no seu programa TI-Basic.
|
Exemplo
Nota: Isto também pode ser utilizado com o Hub TI-Innovator™. |
|
Catálogo > |
|
|
Devolve o resto do primeiro argumento em relação ao segundo argumento conforme definido pelas identidades: remain(x,0) x |
|
|
Por consequência, não se esqueça de que remain(-x,y) - remain(x,y). O resultado é zero ou tem o mesmo sinal do primeiro argumento. Nota: Consulte também mod(), aqui. |
|
|
Catálogo > |
|||||||||||||||||||
|
Programar comando: Interrompe o programa e mostra uma caixa de diálogo com a mensagem CadeiaDePedido e uma caixa de entrada para a resposta do utilizador. Quando o utilizador escrever uma resposta e clicar em OK, os conteúdos da caixa de entrada são atribuídos à variável var. Se o utilizador clicar em Cancelar, o programa continua sem aceitar qualquer entrada. O programa utiliza o valor anterior de var se var já tiver sido definida. O argumento DispFlag opcional podem ser qualquer expressão.
|
Definir um programa: Definir request_demo()=Prgm
Execute o programa e escreva uma resposta: request_demo()
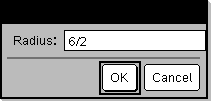
Resultado após selecionar OK: Raio: 6/2 |
||||||||||||||||||
|
O argumento statusVar opcional proporciona uma forma de determinar como o utilizador ignorou a caixa de diálogo. Atente que statusVar requer o argumento DispFlag.
O argumento func() permite que um programa armazene a resposta do utilizador como uma definição de função. Esta sintaxe funciona como se o utilizador executasse o comando: Definir func(arg1, ...argn) = resposta do utilizador O programa pode então usar a função definida func(). A CadeiaDePedido deve guiar o utilizador para introduzir uma resposta de utilizador adequada que complete a definição de função. Nota: Pode utilizar o comando Para parar um programa que contém um comando Pedido dentro de um ciclo infinito:
Nota: Consulte também |
Definir um programa: Definir polynomial()=Prgm
Execute o programa e escreva uma resposta: polynomial()
Resultado depois de introduzir x^3+3x+1 e selecionar OK: As raizes reais são: {-0.322185} |
|
Catálogo > |
|||||||||||||
|
Programar comando: Funciona de forma idêntica à primeira sintaxe do comando Pedido, exceto no facto de a resposta do utilizador ser sempre interpretada como uma cadeia. Em contraste, o comando Pedido interpreta a resposta como uma expressão, a não ser que o utilizador o coloque entre aspas (""). Nota: Pode usar o comando CadeiaDePedido dentro de um programa definido pelo utilizador, mas não dentro de uma função. Para parar um programa que contém um comando
Nota: Consulte também |
Definir um programa: Definir requestStr_demo()=Prgm
Execute o programa e escreva uma resposta: requestStr_demo()
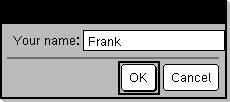
Resultado depois de se selecionar OK (De referir que o argumento DispFlag de 0 omite o pedido e a resposta do histórico):
requestStr_demo() A resposta tem 5 caracteres. |
|
Catálogo > |
|
|
Return [Expr] Devolve Expr como resultado da função. Utilize num bloco Func ... EndFunc. Nota: Utilize Return sem um argumento num bloco Prgm...EndPrgm para sair de um programa. Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto. |
|
|
Catálogo > |
|
|
right(List1[, Num]) ⇒ lista Devolve os elementos Num mais à direita contidos em Lista1. Se omitir Num, devolve todos os elementos de Lista1. |
|
|
right(sourceString[, Num]) ⇒ cadeia Devolve os caracteres Num mais à direita na cadeia de caracteres sourceString Se omitir Num, devolve todos os caracteres de sourceString. |
|
|
right(Comparação) ⇒ expressão Devolve o lado direito de uma equação ou desigualdade. |
|
|
Catálogo > |
|
|
Utiliza o método Runge-Kutta para resolver o sistema Expr é o segundo membro que define a equação diferencial ordinária (EDO). SystemOfExpr é o sistema de segundos membros que definem o sistema de EDOs (corresponde à ordem de variáveis dependentes em ListOfDepVars). ListOfExpr é uma lista de segundos membros que definem o sistema de EDOs (corresponde à ordem de variáveis dependentes em ListOfDepVars). Var é a variável independente. ListOfDepVars é uma lista de variáveis dependentes. {Var0, VarMax} é uma lista de dois elementos que informa a função para integrar de Var0 a VarMax. ListOfDepVars0 é uma lista de valores iniciais para variáveis dependentes. Se VarStep avalia para um número diferente de zero: sinal(VarStep) = sinal(VarMax-Var0) e soluções são apresentadas em Var0+i*VarStep para todos os i=0,1,2,… tal como Var0+i*VarStep está em [var0,VarMax] (pode não obter um valor de solução em VarMax). se VarStep avaliar para zero, as soluções são apresentadas nos valores Var Runge-Kutta". diftol é a tolerância de erro (passa para 0,001). |
Equação diferencial: y'=0.001*y*(100-y) e y(0)=10 Para ver o resultado completo, prima 5 e, de seguida, utilize 7 e 8 para mover o cursor. Mesma equação com diftol definido para 1.E-6 Compare o resultado acima com a solução exacta CAS obtida através de deSolve() e seqGen():
Sistema de equações:
com y1(0)=2 e y2(0)=5
|
|
Catálogo > |
|
|
root(Expr) ⇒ raiz
root(Expr1, Expr2) devolve a raiz de Expr2 de Expr1. Expr1 pode ser uma constante de ponto flutuante complexa, uma constante racional complexa ou número inteiro, ou uma expressão simbólica geral. Nota: Consulte também Modelo da raiz de índice N, aqui. |
|
|
Catálogo > |
|
|
rotate(NúmeroInteiro1[, #deRotações]) ⇒ número inteiro Roda os bits num número inteiro binário. Pode introduzir NúmeroInteiro1 em qualquer base numérica; é convertido automaticamente para uma forma binária de 64 bits assinada. Se a magnitude de NúmeroInteiro1 for demasiado grande para esta forma, uma operação do módulo simétrico coloca-o no intervalo. (Para mais informações, consulte ►Base2, aqui. |
No modo base Bin:
Para ver o resultado completo, prima 5 e, de seguida, utilize 7 e 8 para mover o cursor. |
|
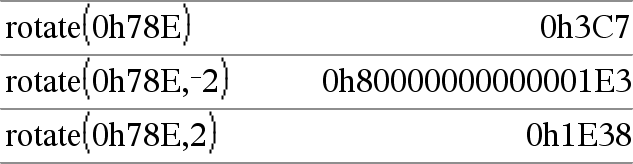
Se #deRotações for positivo, a rotação é para a esquerda. Se #deRotações for negativo, a rotação é para a direita. A predefinição é -1 (rodar um elemento para a direita). Por exemplo, numa rotação para a direita: |
No modo base Hex:
|
|
Cada bit roda para a direita. 0b00000000000001111010110000110101 O bit mais à direita roda para o extremo esquerdo. produz: 0b10000000000000111101011000011010 Os resultados aparecem de acordo com o modo base. |
Importante: Para introduzir um número binário ou hexadecimal, utilize sempre o prefixo 0b ou 0h (zero, não a letra O). |
|
rotate(Lista1[, #deRotações]) ⇒ lista Devolve uma cópia de Lista1 rodada para a direita ou para a esquerda pelos elementos #deRotações. Não altera Lista1. Se #deRotações for positivo, a rotação é para a esquerda. Se #deRotações for negativo, a rotação é para a direita. A predefinição é -1 (rodar um elemento para a direita). |
No modo base Dec:
|
|
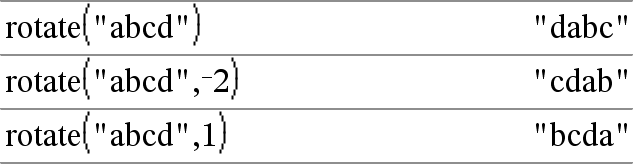
rotate(Cadeia1[,#deRotações]) ⇒ cadeia Devolve uma cópia de Cadeia1 rodada para a direita ou para a esquerda pelos caracteres #deRotações. Não altere Cadeia1. Se #deRotações for positivo, a rotação é para a esquerda. Se #deRotações for negativo, a rotação é para a direita. A predefinição é -1 (rodar um carácter para a direita). |
|
|
Catálogo > |
|
|
round(Expr1[, dígitos]) ⇒ expressão Devolve o argumento arredondado para o número especificado de dígitos após o ponto decimal. dígitos tem de ser um número inteiro no intervalo 0–12. Se dígitos não for incluído, devolve o argumento arredondado para 12 dígitos significativos. Nota: A visualização do modo de dígitos pode afetar como este é apresentado. |
|
|
round (Lista1[, dígitos]) ⇒ lista Devolve uma lista dos elementos arredondada para o número especificado de dígitos. |
|
|
round (Matriz1[, dígitos]) ⇒ matriz Devolve uma matriz dos elementos arredondados para o número especificado de dígitos. |
|
|
Catálogo > |
|
|
rowAdd(Matriz1, rIndex1, rIndex2) ⇒ matriz Devolve uma cópia de Matriz1 com a linha rIndex2 substituída pela soma das linhas rIndex1 e rIndex2. |
|
|
Catálogo > |
|
|
rowDim(Matriz) ⇒ expressão Devolve o número de linhas em Matriz. Nota: Consulte também colDim(), aqui. |
|
|
Catálogo > |
|
|
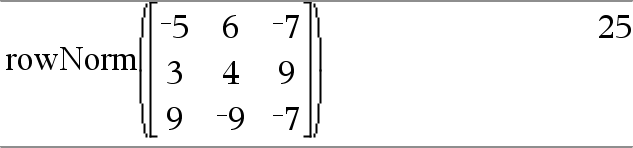
rowNorm(Matriz) ⇒ expressão Devolve o máximo das somas dos valores absolutos dos elementos nas linhas em Matriz. Nota: Todos os elementos da matriz têm de ser simplificados para números. Consulte também colNorm(), aqui. |
|
|
Catálogo > |
|
|
rowSwap (Matriz1, rIndex1, rIndex2) ⇒ matriz Devolve Matriz1 com as linhas rIndex1 e rIndex2 trocadas. |
|
|
Catálogo > |
|||||||
|
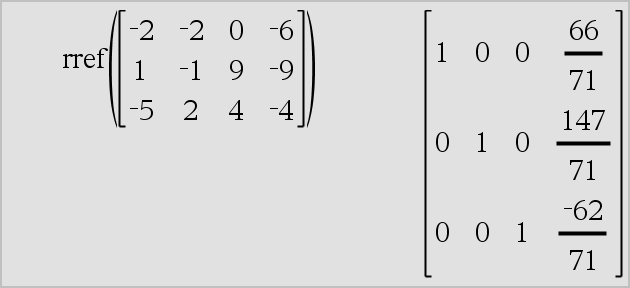
rref(Matriz1[, Tol]) ⇒ matriz Devolve a forma de escalão-linha reduzida de Matriz1. |
|
||||||
|
Opcionalmente, qualquer elemento da matriz é tratado como zero se o valor absoluto for inferior a Tol. Esta tolerância é utilizada apenas se a matriz tiver entradas de ponto flutuante e não contiver nenhuma variável simbólica sem nenhum valor atribuído. Caso contrário, Tol é ignorado.
Nota: Consulte também ref(), aqui. |
|