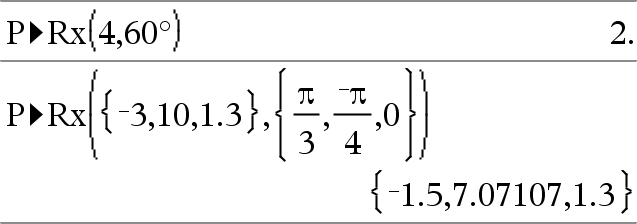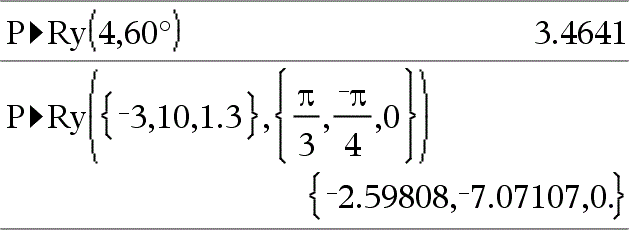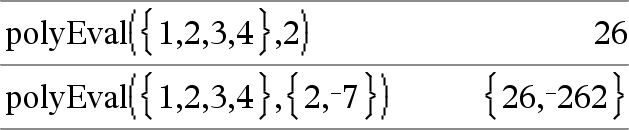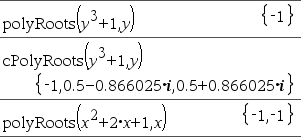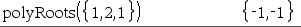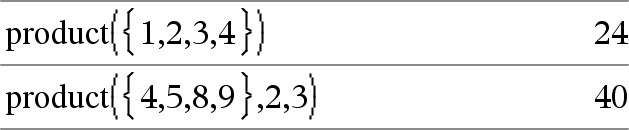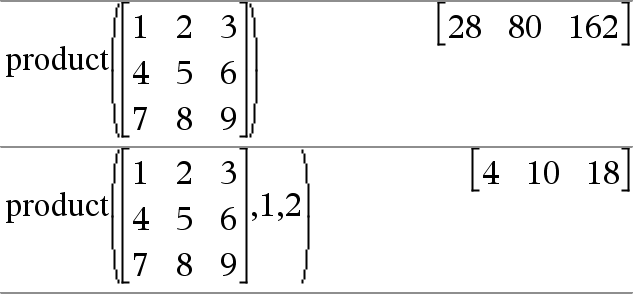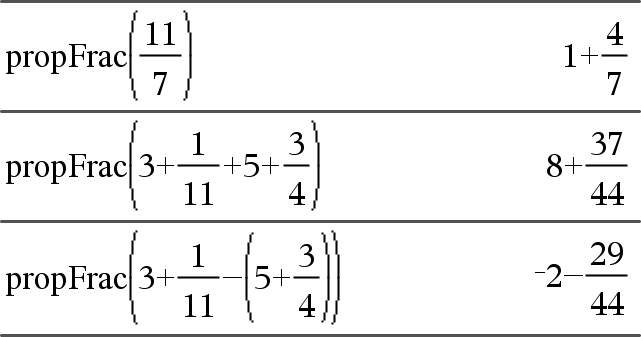P

P4Rx()

Catálogo >

P4Rx(rExpr, qExpr) Þexpressão

P4Rx(rList, qList) Þlista

P4Rx(rMatrix, qMatrix) Þmatriz

Devolve a coordenada x equivalente do par (r, q).

Nota: O argumento q é interpretado como um ângulo expresso em graus, gradianos ou radianos de acordo com o modo de ângulo actual. Se o argumento for uma expressão, pode utilizar ¡, G ou R para substituir a definição do modo de ângulo temporariamente.

Nota: Pode introduzir esta função através da escrita de P@>Rx(...) no teclado do computador.

No modo de ângulo Radianos:

P4Ry()

Catálogo >

P4Ry(rValue, qValue) Þvalor

P4Ry(rList, qList) Þlista

P4Ry(rMatrix, qMatrix) Þmatriz

Devolve a coordenada y equivalente do par (r, q).

Nota: O argumento q é interpretado como um ângulo expresso em graus, gradianos ou radianos de acordo com o modo de ângulo actual.

Nota: Pode introduzir esta função através da escrita de P@>Ry(...) no teclado do computador.

No modo de ângulo Radianos:

PassErr

Catálogo >

PassErr

Passa um erro para o nível seguinte.

Se a variável do sistema errCode for zero, PassErr não faz nada.

A proposição Else do bloco Try...Else...EndTry deve utilizar ClrErr ou PassErr. Se tiver de processar ou ignorar o erro, utilize ClrErr. Se não souber o que fazer com o erro, utilize PassErr para o enviar para a rotina de tratamento de erros seguinte. Se não existirem mais rotinas de tratamento de erros Try...Else...EndTry pendente, a caixa de diálogo de erros aparecerá como normal.

Nota: Consulte também ClrErr, aqui, e Try, aqui.

Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

Para ver um exemplo de PassErr, consulte o exemplo 2 no comando Try, aqui.

piecewise()

Catálogo >

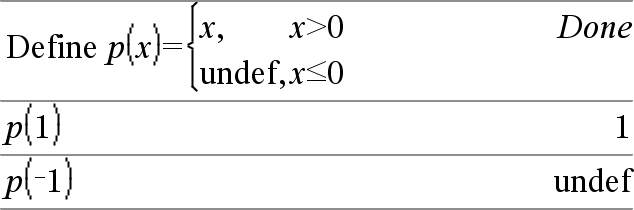
piecewise(Expr1 [, Condição1 [, Expr2 [, Condição2 [, … ]]]])

Devolve as definições para uma função piecewise na forma de uma lista. Pode também criar definições piecewise com um modelo.

Nota: Consulte também Modelo de Função por ramos, aqui.

poissCdf()

Catálogo >

poissCdf(l,LimiteInferior,LimiteSuperior)Þnúmero se LimiteInferior e LimiteSuperior forem números, lista se LimiteInferior e LimiteSuperior forem listas

poissCdf(l,LimiteSuperior)(para P(0{X{LimiteSuperior)Þnúmero se LimiteSuperior for um número, lista se LimiteSuperior for uma lista

Calcula uma probabilidade cumulativa para a distribuição Poisson discreta com a média especificada l.

Para P(X { LimiteSuperior), defina LimiteInferior=0

 

poissPdf()

Catálogo >

poissPdf(l, ValX) Þnúmero se ValX for um número, lista se ValX for uma lista

Calcula uma probabilidade para a distribuição Poisson discreta com a média especificada l.

 

►Polar

Catálogo >

Vector ►Polar

Nota: Pode introduzir este operador através da escrita de @>Polar no teclado do computador.

Apresenta o vector em forma polar [r∠θ]. O vector tem de ser de dimensão 2 e pode ser uma linha ou uma coluna.

Nota: ►Polar é uma instrução de formato de visualização, não uma função de conversão. Só pode utilizá-la no fim de uma linha de entrada e não actualiza ans.

Nota: Consulte também ►Rect, aqui.

ValorComplexo 4Polar

Apresenta VectorComplexo em forma polar.

• O modo de ângulo Graus devolve (r∠θ).
• O modo de ângulo Radianos devolve reiθ.

ValorComplexo pode ter qualquer forma complexa. No entanto, uma entrada reiθ provoca um erro no modo de ângulo Graus.

Nota: Tem de utilizar os parêntesis para uma entrada polar (r∠θ).

No modo de ângulo Radianos:

 

No modo de ângulo Gradianos:

 

No modo de ângulo Graus:

polyEval()

Catálogo >

polyEval(Lista1, Expr1) Þexpressão

polyEval(Lista1, Lista2) Þexpressão

Interpreta o primeiro argumento como o coeficiente de um polinómio de grau descendente e devolve o polinómio avaliado para o valor do segundo argumento.

polyRoots()

Catálogo >

polyRoots(Poli,Var) Þlista

polyRoots(ListaDeCoeficientes) Þlista

A primeira sintaxe, polyRoots(Poli,Var), devolve uma lista de raízes reais do polinómio Poly em relação à variável Var. Se não existirem raízes reais, devolve uma lista vazia: { }.

Poly tem de ser um polinómio na forma expandida. Não utilize formatos não expandidos, como, por exemplo, y2·y+1 ou x·x+2·x+1

A segunda sintaxe, polyRoots(ListaDeCoeficientes), devolve uma lista de raízes reais para os coeficientes em ListaDeCoeficientes.

Nota: Consulte também cPolyRoots(), aqui.

PowerReg

Catálogo >

PowerReg X,Y [, Freq] [, Categoria, Incluir]]

Calcula a regressão de potênciay = (a·(x)b)nas listas X e Y com a frequência Freq. Um resumo dos resultados é guardado na variável stat.results (aqui).

Todas as listas têm de ter a mesma dimensão, excepto para Incluir.

X e Y são listas de variáveis independentes e dependentes.

Freq é uma lista opcional de valores de frequência. Cada elemento em Freq especifica a frequência de ocorrência para cada ponto de dados X e Y correspondente. O valor predefinido é 1. Todos os elementos têm de ser números inteiros 0.

Categoria é uma lista de códigos de categorias numéricos ou de cadeias para os dados X e Y correspondentes.

Incluir é uma lista de um ou mais códigos de categorias. Apenas os itens de dados cujo código de categoria está incluído nesta lista são considerados no cálculo.

Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (aqui).

 

Variável de saída

Descrição

stat.RegEqn

Equação de regressão: a·(x)b

stat.a, stat.b

Parâmetros de regressão

stat.r2

Coeficiente de determinação linear para dados transformados

stat.r

Coeficiente de correlação para dados transformados (ln(x), ln(y))

stat.Resid

Resíduos associados ao modelo de potência

stat.ResidTrans

Resíduos associados ao ajuste linear dos dados transformados

stat.XReg

Lista de dados na Lista X modificada utilizada na regressão com base nas restrições de Freq, Lista de categorias e Incluir categorias

stat.YReg

Lista de dados na Lista Y modificada utilizada na regressão com base nas restrições de Freq, Lista de categorias e Incluir categorias

stat.FreqReg

Lista de frequências correspondentes a stat.XReg e stat.YReg

Prgm

Catálogo >

Prgm

     Bloco

EndPrgm

Modelo para criar um programa definido pelo utilizador. Tem de ser utilizado o comando Define, Define BibPub ou Define BibPriv.

Bloco pode ser uma afirmação, uma série de afirmações separadas pelo carácter “:” ou uma série de afirmações em linhas separadas.

Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

Calcule o GCD e visualize os resultados intermédios.

prodSeq()

Consulte P ( ), aqui.

 

 

Produto (PI)

Consulte P (), aqui.

 

 

product()

Catálogo >

product(Lista [, Início [, fim ]]) Þexpressão

Apresenta o produto dos elementos contidos na Lista. Início e Fim são opcionais. Especificam um intervalo de elementos.

product(Matriz1 [, Início [, fim ]]) Þmatriz

Devolve um vector da linha com os produtos dos elementos nas colunas de Matriz1. Início e Fim são opcionais. Especificam um intervalo de linhas.

Os elementos (nulos) vazios são ignorados. Para mais informações sobre os elementos vazios, consulte aqui.

propFrac()

Catálogo >

propFrac(Valor1 [, Var ]) Þvalor

propFrac(rational_number) devolve rational_number como a soma de um número inteiro e uma fracção com o mesmo sinal e uma magnitudade do denominador maior que a magnitude do numerador.

propFrac(rational_expression, Var) devolve a soma das fracções adequadas e um polinómio em relação a Var. O grau de Var no denominador excede o grau de Var no numerador em cada fracção adequada. As potências similares de Var são recolhidas. Os termos e os factores são ordenados com Var como variável principal.

Se omitir Var, uma expansão da fracção adequada é efectuada em relação à variável principal. Os coeficientes da parte polinominal são efectuados adequadamente em relação à primeira variável principal, etc.

Pode utilizar a função propFrac() para representar as fracções mistas e demonstrar a adição e a subtracção de fracções mistas.