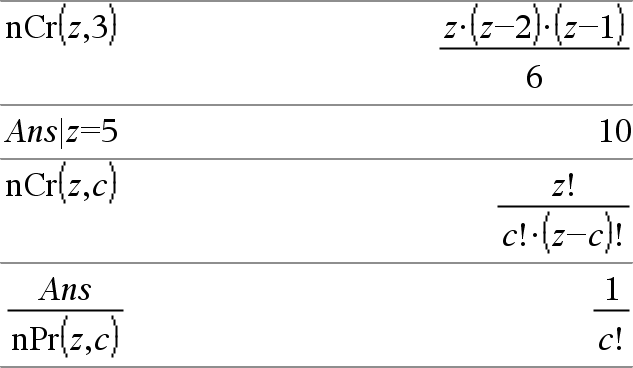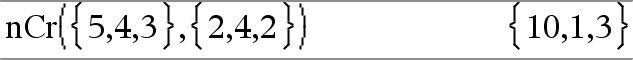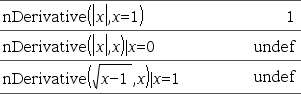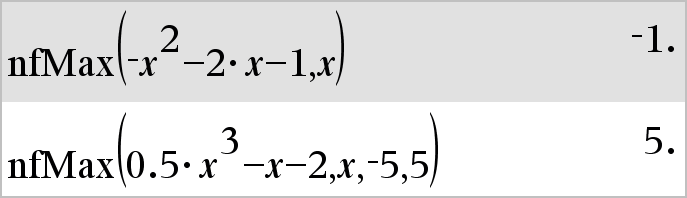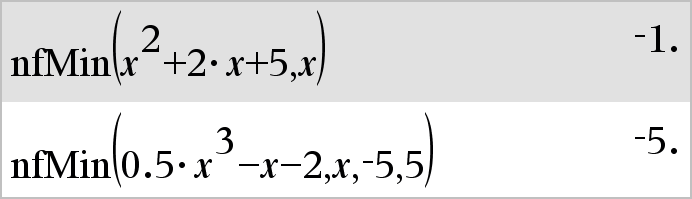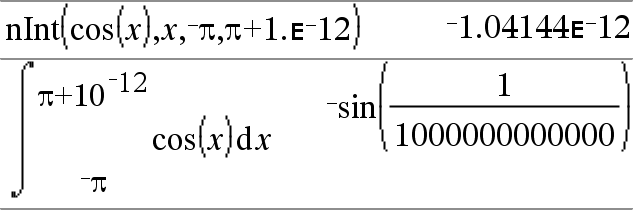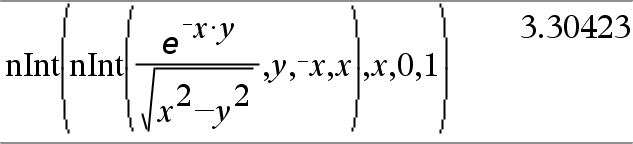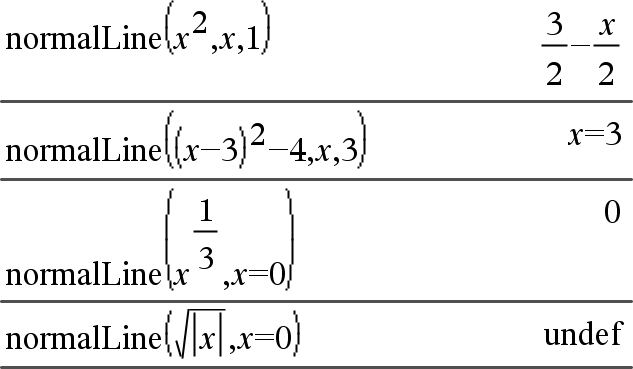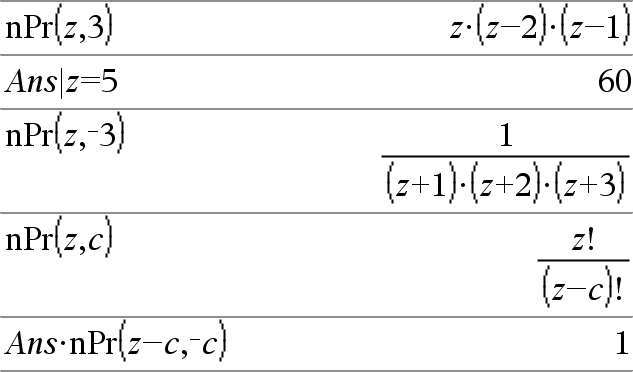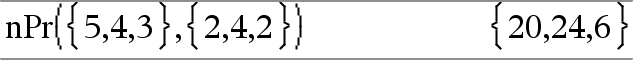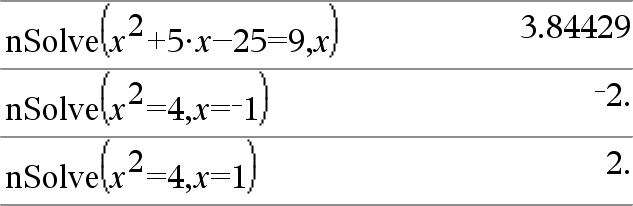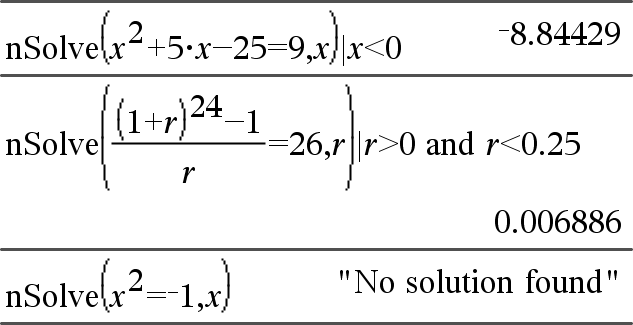|
touches /= |
|
|
BooleanExpr1 BooleanList1 BooleanMatrix1
Renvoie la négation d'une opération logique and sur les deux arguments. Renvoie true (vrai) ou false (faux) ou une forme simplifiée de l'équation. Pour les listes et matrices, renvoie le résultat des comparaisons, élément par élément. |
|
|
Integer1 Compare les représentations binaires de deux entiers en appliquant une opération nand. En interne, les deux entiers sont convertis en nombres binaires 64 bits signés. Lorsque les bits comparés correspondent, le résultat est 0 si dans les deux cas il s'agit d'un bit 1 ; dans les autres cas, le résultat est 1. La valeur donnée représente le résultat des bits et elle est affichée selon le mode de base utilisé. Les entiers peuvent être entrés dans tout type de base. Pour une entrée binaire ou hexadécimale, vous devez utiliser respectivement le préfixe 0b ou 0h. Tout entier sans préfixe est considéré comme un nombre en écriture décimale (base 10). |
|
|
Catalogue > |
|
|
nCr(Expr1, Expr2)Þexpression Pour les expressions Expr1 et Expr2 avec Expr1 | Expr2 | 0, nCr() donne le nombre de combinaisons de Expr1 éléments pris parmi Expr2 éléments. (Appelé aussi « coefficient binomial ».) Les deux arguments peuvent être des entiers ou des expressions symboliques. nCr(Expr, 0)Þ1 nCr(Expr, entierNég)Þ0 nCr(Expr, entierPos)Þ Expr·(ExprN1)... (ExprNentierPos+1)/ entierPos! nCr(Expr, nonEntier)Þexpression!/ ((ExprNnonEntier)!·nonEntier!) |
|
|
nCr(Liste1, Liste2)Þliste Donne une liste de combinaisons basées sur les paires d'éléments correspondantes dans les deux listes. Les arguments doivent être des listes comportant le même nombre d'éléments. |
|
|
nCr(Matrice1, Matrice2)Þmatrice Donne une matrice de combinaisons basées sur les paires d'éléments correspondantes dans les deux matrices. Les arguments doivent être des matrices comportant le même nombre d'éléments. |
|
|
Catalogue > |
|
|
Affiche la dérivée numérique calculée avec les méthodes de différenciation automatique. Quand la valeur est spécifiée, celle-ci prévaut sur toute affectation de variable ou substitution précédente de type « | » pour la variable. L'ordre de la dérivée doit être 1 ou 2. |
|
|
Catalogue > |
|
|
newList(nbreÉléments)Þliste Donne une liste de dimension nbreÉléments. Tous les éléments sont nuls. |
|
|
Catalogue > |
|
|
newMat(nbreLignes, nbreColonnes)Þmatrice Donne une matrice nulle de dimensions nbreLignes, nbreColonnes. |
|
|
Catalogue > |
|
|
nfMax(Expr, Var)Þvaleur nfMax(Expr, Var, LimitInf)Þvaleur nfMax(Expr, Var, LimitInf, LimitSup)Þvaleur nfMax(Expr, Var) | LimitInf{Var{LimitSupÞvaleur Donne la valeur numérique possible de la variable Var au point où le maximum local de Expr survient. Si LimitInf et LimitSup sont spécifiés, la fonction recherche le maximum local dans l'intervalle fermé [LimitInf,LimitSup].
|
|
|
Catalogue > |
|
|
nfMin(Expr, Var)Þvaleur nfMin(Expr, Var, LimitInf)Þvaleur nfMin(Expr, Var, LimitInf, LimitSup)Þvaleur nfMin(Expr, Var) | LimitInf{Var{LimitSupÞvaleur Donne la valeur numérique possible de la variable Var au point où le minimum local de Expr survient. Si LimitInf et LimitSup sont spécifiés, la fonction recherche le minimum local dans l'intervalle fermé [LimitInf,LimitSup].
|
|
|
Catalogue > |
|
|
nInt(Expr1, Var, Borne1, Borne2)Þexpression Si l'intégrande Expr1 ne contient pas d'autre variable que Var et si Borne1 et Borne2 sont des constantes, en +ˆ ou en -ˆ, alors nInt() donne le calcul approché de ‰(Expr1, Var, Borne1, Borne2). Cette approximation correspond à une moyenne pondérée de certaines valeurs d'échantillon de l'intégrande dans l'intervalle Borne1<Var<Borne2. |
|
|
L'objectif est d'atteindre une précision de six chiffres significatifs. L'algorithme s'adaptant, met un terme au calcul lorsqu'il semble avoir atteint cet objectif ou lorsqu'il paraît improbable que des échantillons supplémentaires produiront une amélioration notable. Le message « Précision incertaine » s'affiche lorsque cet objectif ne semble pas atteint. |
|
|
Il est possible de calculer une intégrale multiple en imbriquant plusieurs appels nInt(). Les bornes d'intégration peuvent dépendre des variables d'intégration les plus extérieures. |
|
|
Remarque : voir aussi ‰(), ici. |
|
|
Catalogue > |
|
|
nom(tauxEffectif,CpY)Þvaleur Fonction financière permettant de convertir le taux d'intérêt effectif tauxEffectif à un taux annuel nominal, CpY étant le nombre de périodes de calcul par an. tauxEffectif doit être un nombre réel et CpY doit être un nombre réel > 0. Remarque : voir également eff(), ici. |
|
|
touches /= |
|
|
BooleanExpr1
BooleanList1
BooleanMatrix1
Renvoie la négation d'une opération logique or sur les deux arguments. Renvoie true (vrai) ou false (faux) ou une forme simplifiée de l'équation. Pour les listes et matrices, renvoie le résultat des comparaisons, élément par élément. |
|
|
Integer1
Compare les représentations binaires de deux entiers en appliquant une opération nor. En interne, les deux entiers sont convertis en nombres binaires 64 bits signés. Lorsque les bits comparés correspondent, le résultat est 1 si dans les deux cas il s'agit d'un bit 1 ; dans les autres cas, le résultat est 0. La valeur donnée représente le résultat des bits et elle est affichée selon le mode de base utilisé. Les entiers peuvent être entrés dans tout type de base. Pour une entrée binaire ou hexadécimale, vous devez utiliser respectivement le préfixe 0b ou 0h. Tout entier sans préfixe est considéré comme un nombre en écriture décimale (base 10). |
|
|
Catalogue > |
|
|
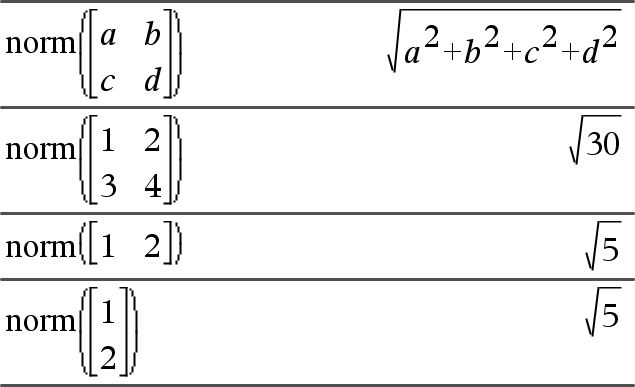
norm(Matrice)Þexpression norm(Vecteur)Þexpression Donne la norme de Frobenius. |
|
|
Catalogue > |
|
|
normalLine(Expr1,Var,Point)Þexpression normalLine(Expr1,Var=Point)Þexpression Donne la normale à la courbe représentée par Expr1 au point spécifié par Var=Point. Assurez-vous de ne pas avoir affecté une valeur à la variable indépendante. Par exemple, si f1(x):=5 et x:=3, alors normalLine(f1(x),x,2) retourne « faux». |
|
|
Catalogue > |
|
|
normCdf(lowBound,upBound[,m[,s]])Þnombre si lowBound et upBound sont des nombres, liste si lowBound et upBound sont des listes Calcule la probabilité qu'une variable suivant la loi normale de moyenne (m, valeur par défaut =0) et d'écart-type (sigma, valeur par défaut = 1) prenne des valeurs entre les bornes lowBound et upBound. Pour P(X { upBound), définissez lowBound = .ˆ. |
|
|
Catalogue > |
|
|
normPdf(ValX[,m[,s]])Þnombre si ValX est un nombre, liste si ValX est une liste Calcule la densité de probabilité de la loi normale à la valeur ValX spécifiée pour les paramètres m et s. |
|
|
Catalogue > |
|
|
not Expr booléenne1ÞExpression booléenne Donne true (vrai) ou false (faux) ou une forme simplifiée de l'argument. |
|
|
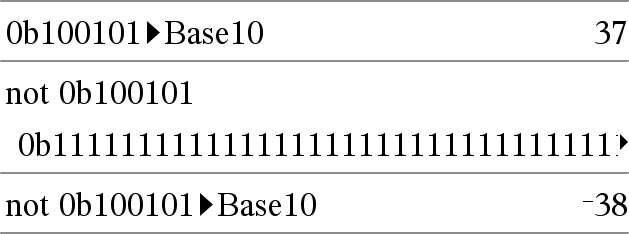
not Entier1Þentier Donne le complément à 1 d'un entier. En interne, Entier1 est converti en nombre binaire 64 bits signé. La valeur de chaque bit est inversée (0 devient 1, et vice versa) pour le complément à 1. Le résultat est affiché en fonction du mode Base utilisé. Les entiers de tout type de base sont admis. Pour une entrée binaire ou hexadécimale, vous devez utiliser respectivement le préfixe 0b ou 0h. Tout entier sans préfixe est considéré comme un nombre en écriture décimale (base 10). Si vous entrez un nombre dont le codage binaire signé dépasse 64 bits, il est ramené à l'aide d'une congruence dans la plage appropriée. Pour de plus amples informations, voir 4Base2, ici. |
En mode base Hex : Important : utilisez le chiffre zéro et pas la lettre O.
En mode base Bin :
Pour afficher le résultat entier, appuyez sur 5, puis utilisez les touches 7 et 8 pour déplacer le curseur. Remarque : une entrée binaire peut comporter jusqu'à 64 chiffres (sans compter le préfixe 0b) ; une entrée hexadécimale jusqu'à 16 chiffres. |
|
Catalogue > |
|
|
nPr(Expr1, Expr2)Þexpression Pour les expressions Expr1 et Expr2 avec Expr1 | Expr2 | 0, nPr() donne le nombre de permutations de Expr1 éléments pris parmi Expr2 éléments. Les deux arguments peuvent être des entiers ou des expressions symboliques. nPr(Expr, 0)Þ1 nPr(Expr, entierNég)Þ 1/((Expr+1)·(Expr+2)... (expressionNentierNég)) nPr(Expr, entierPos) Þ Expr·(ExprN1)... (ExprNentierPos+1) nPr(Expr, nonEntier)ÞExpr! / (ExprNnonEntier)! |
|
|
nPr(Liste1, Liste2)Þliste Donne une liste de permutations basées sur les paires d'éléments correspondantes dans les deux listes. Les arguments doivent être des listes comportant le même nombre d'éléments. |
|
|
nPr(Matrice1, Matrice2)Þmatrice Donne une matrice de permutations basées sur les paires d'éléments correspondantes dans les deux matrices. Les arguments doivent être des matrices comportant le même nombre d'éléments. |
|
|
Catalogue > |
|
|
npv(tauxIntérêt,MTO,ListeMT[,FréqMT]) Fonction financière permettant de calculer la valeur actuelle nette ; la somme des valeurs actuelles des mouvements d'entrée et de sortie de fonds. Un résultat positif pour NPV indique un investissement rentable. tauxIntérêt est le taux à appliquer pour l'escompte des mouvements de trésorerie (taux de l'argent) sur une période donnée. MT0 correspond au mouvement de trésorerie initial à l'heure 0 ; il doit s'agir d'un nombre réel. Liste MT est une liste des montants de mouvements de trésorerie après le mouvement de trésorerie initial MT0. FréqMT est une liste dans laquelle chaque élément indique la fréquence d'occurrence d'un montant de mouvement de trésorerie groupé (consécutif), correspondant à l'élément de ListeMT. La valeur par défaut est 1 ; si vous saisissez des valeurs, elles doivent être des entiers positifs < 10 000. |
|
|
Catalogue > |
|
|
nSolve(Équation,Var[=Condition])Þ chaîne_nombre ou erreur nSolve(Équation,Var[=Condition],LimitInf) Þchaîne_nombre ou erreur nSolve(Équation,Var[=Condition],LimitInf,LimitSup) Þchaîne_nombre ou erreur nSolve(Équation,Var[=Condition]) | LimitInf{Var{LimitSup Þchaîne_nombre ou erreur Recherche de façon itérative une solution numérique réelle approchée pour Équation en fonction de sa variable. Spécifiez la variable comme suit : variable – ou – variable = nombre réel Par exemple, x est autorisé, de même que x=3. |
Remarque : si plusieurs solutions sont possibles, vous pouvez utiliser une condition pour mieux déterminer une solution particulière. |
|
nSolve() tente de déterminer un point où la valeur résiduelle est zéro ou deux points relativement rapprochés où la valeur résiduelle a un signe négatif et où son ordre de grandeur n'est pas excessif. S'il n'y parvient pas en utilisant un nombre réduit de points d'échantillon, la chaîne « Aucune solution n'a été trouvée » s'affiche.
|
|