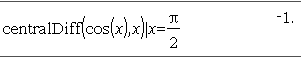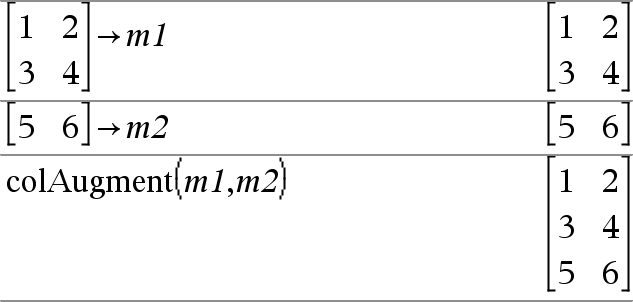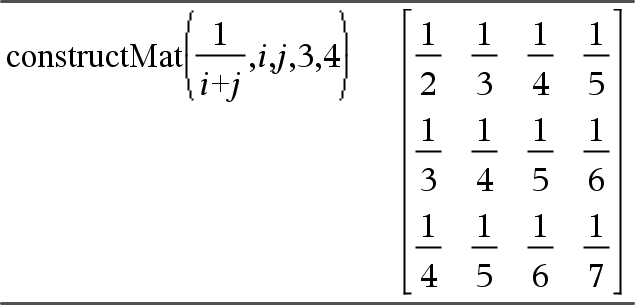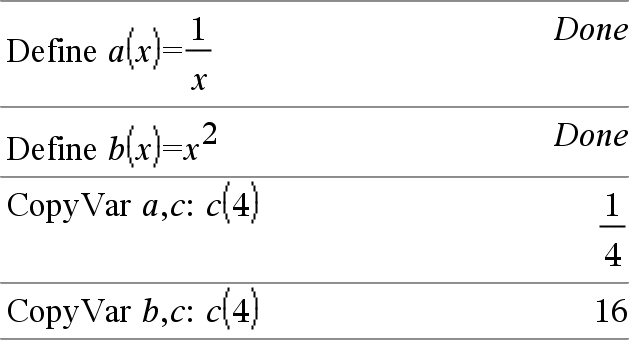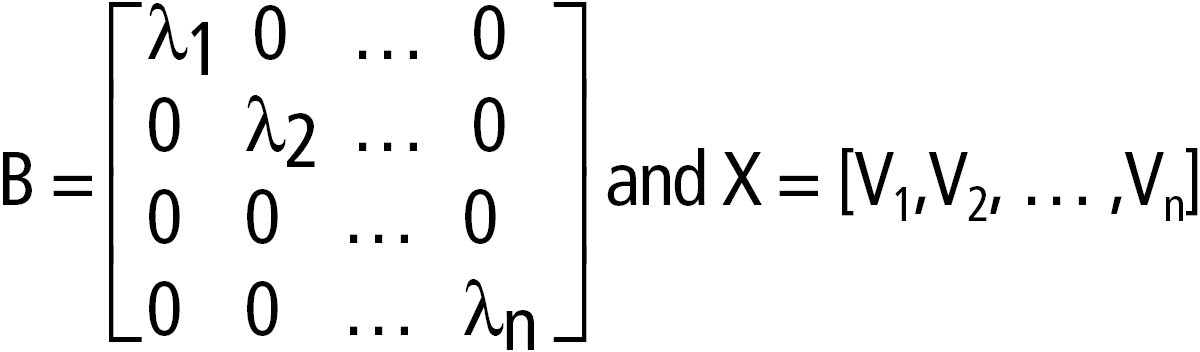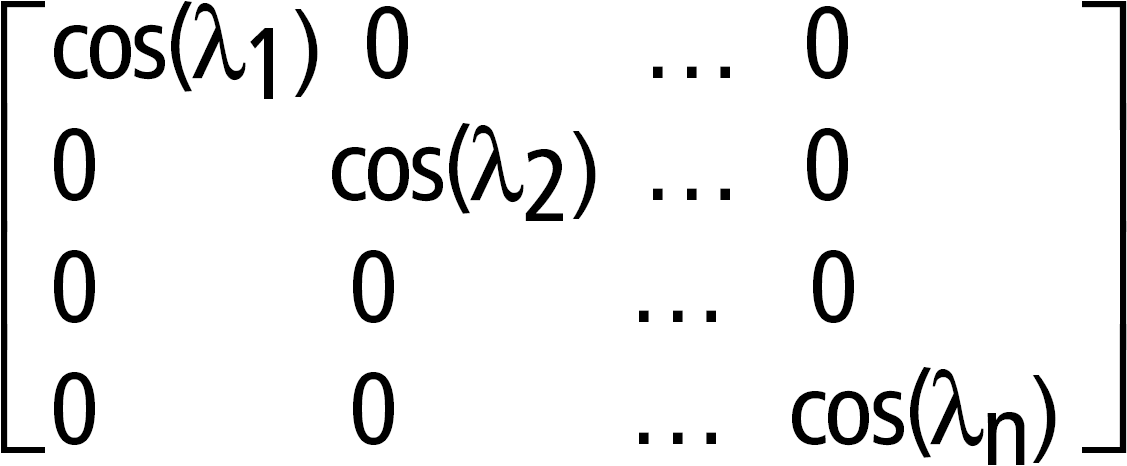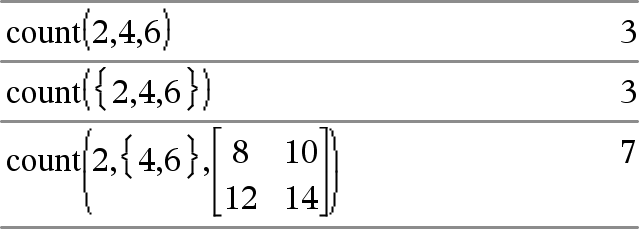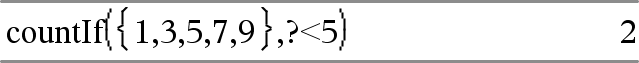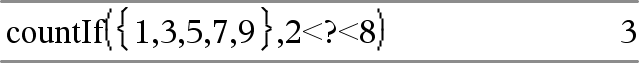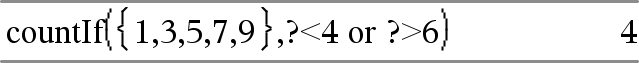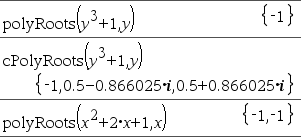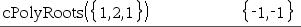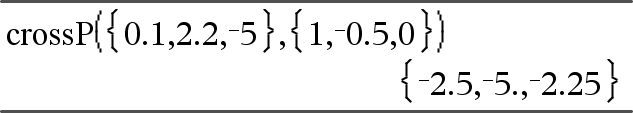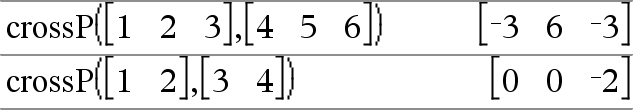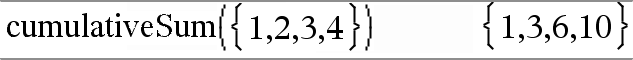|
Catalog > |
|
|
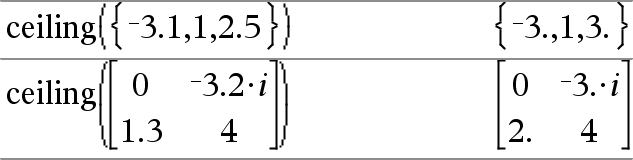
ceiling(Value1) ⇒ value Returns the nearest integer that is ≥ the argument. The argument can be a real or a complex number. Note: See also floor(). |
|
|
ceiling(List1) ⇒ list Returns a list or matrix of the ceiling of each element. |
|
|
Catalog > |
|
|
Returns the numerical derivative using the central difference quotient formula. When Value is specified, it overrides any prior variable assignment or any current “|” substitution for the variable. Step is the step value. If Step is omitted, it defaults to 0.001. When using List1 or Matrix1, the operation gets mapped across the values in the list or across the matrix elements. Note: See also avgRC(). |
|
|
Catalog > |
|
|
char(Integer) ⇒ character Returns a character string containing the character numbered Integer from the handheld character set. The valid range for Integer is 0–65535. |
|
|
Catalog > |
|
|
χ22way obsMatrix chi22way obsMatrix Computes a χ2 test for association on the two-way table of counts in the observed matrix obsMatrix. A summary of results is stored in the stat.results variable. (here) For information on the effect of empty elements in a matrix, see “Empty (Void) Elements,” here. |
|
|
Output variable |
Description |
|
stat.χ2 |
Chi square stat: sum (observed - expected)2/expected |
|
stat.PVal |
Smallest level of significance at which the null hypothesis can be rejected |
|
stat.df |
Degrees of freedom for the chi square statistics |
|
stat.ExpMat |
Matrix of expected elemental count table, assuming null hypothesis |
|
stat.CompMat |
Matrix of elemental chi square statistic contributions |
|
Catalog > |
|
|
χ2Cdf(lowBound,upBound,df) ⇒ number if lowBound and upBound are numbers, list if lowBound and upBound are lists chi2Cdf(lowBound,upBound,df) ⇒ number if lowBound and upBound are numbers, list if lowBound and upBound are lists Computes the χ2 distribution probability between lowBound and upBound for the specified degrees of freedom df. For P(X ≤ upBound), set lowBound = 0. For information on the effect of empty elements in a list, see “Empty (Void) Elements,” here. |
|
|
Catalog > |
|
|
χ2GOF obsList,expList,df chi2GOF obsList,expList,df Performs a test to confirm that sample data is from a population that conforms to a specified distribution. obsList is a list of counts and must contain integers. A summary of results is stored in the stat.results variable. (See here.) For information on the effect of empty elements in a list, see “Empty (Void) Elements,” here. |
|
|
Output variable |
Description |
|
stat.χ2 |
Chi square stat: sum((observed - expected)2/expected |
|
stat.PVal |
Smallest level of significance at which the null hypothesis can be rejected |
|
stat.df |
Degrees of freedom for the chi square statistics |
|
stat.CompList |
Elemental chi square statistic contributions |
|
Catalog > |
|
|
χ2Pdf(XVal,df) ⇒ number if XVal is a number, list if XVal is a list chi2Pdf(XVal,df) ⇒ number if XVal is a number, list if XVal is a list Computes the probability density function (pdf) for the χ2 distribution at a specified XVal value for the specified degrees of freedom df. For information on the effect of empty elements in a list, see “Empty (Void) Elements,” here. |
|
|
Catalog > |
|
|
ClearAZ Clears all single-character variables in the current problem space. If one or more of the variables are locked, this command displays an error message and deletes only the unlocked variables. See |
|
|
Catalog > |
|
|
Clears the error status and sets system variable errCode to zero. The Else clause of the Try...Else...EndTry block should use ClrErr or PassErr. If the error is to be processed or ignored, use ClrErr. If what to do with the error is not known, use PassErr to send it to the next error handler. If there are no more pending Try...Else...EndTry error handlers, the error dialog box will be displayed as normal. Note: See also PassErr, here, and Try, here. Note for entering the example: For instructions on entering multi-line program and function definitions, refer to the Calculator section of your product guidebook. |
For an example of ClrErr, See Example 2 under the Try command, here.
|
|
Catalog > |
|
|
colAugment(Matrix1, Matrix2) ⇒ matrix Returns a new matrix that is Matrix2 appended to Matrix1. The matrices must have equal column dimensions, and Matrix2 is appended to Matrix1 as new rows. Does not alter Matrix1 or Matrix2. |
|
|
Catalog > |
|
|
colDim(Matrix) ⇒ expression Returns the number of columns contained in Matrix. Note: See also rowDim(). |
|
|
Catalog > |
|
|
colNorm(Matrix) ⇒ expression Returns the maximum of the sums of the absolute values of the elements in the columns in Matrix. Note: Undefined matrix elements are not allowed. See also rowNorm(). |
|
|
Catalog > |
|
|
conj(Value1) ⇒ value conj(List1) ⇒ list conj(Matrix1) ⇒ matrix Returns the complex conjugate of the argument. |
|
|
Catalog > |
|
|
constructMat(Expr,Var1,Var2,numRows,numCols) ⇒ matrix Returns a matrix based on the arguments. Expr is an expression in variables Var1 and Var2. Elements in the resulting matrix are formed by evaluating Expr for each incremented value of Var1 and Var2. Var1 is automatically incremented from 1 through numRows. Within each row, Var2 is incremented from 1 through numCols. |
|
|
Catalog > |
|
|
CopyVar Var1, Var2 CopyVar Var1., Var2. CopyVar Var1, Var2 copies the value of variable Var1 to variable Var2, creating Var2 if necessary. Variable Var1 must have a value. If Var1 is the name of an existing user-defined function, copies the definition of that function to function Var2. Function Var1 must be defined. Var1 must meet the variable-naming requirements or must be an indirection expression that simplifies to a variable name meeting the requirements. |
|
|
CopyVar Var1., Var2. copies all members of the Var1. variable group to the Var2. group, creating Var2. if necessary. Var1. must be the name of an existing variable group, such as the statistics stat.nn results, or variables created using the |
|
|
Catalog > |
|
|
corrMat(List1,List2[,…[,List20]]) Computes the correlation matrix for the augmented matrix [List1, List2, ..., List20]. |
|
|
µ key |
|
|
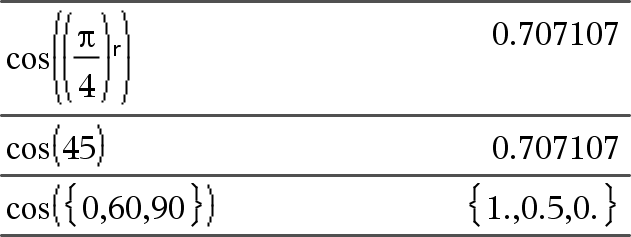
cos(Value1) ⇒ value cos(List1) ⇒ list
cos(List1) returns a list of the cosines of all elements in List1. Note: The argument is interpreted as a degree, gradian or radian angle, according to the current angle mode setting. You can use °, G, or r to override the angle mode temporarily. |
In Degree angle mode:
In Gradian angle mode:
In Radian angle mode:
|
|
cos(squareMatrix1) ⇒ squareMatrix Returns the matrix cosine of squareMatrix1. This is not the same as calculating the cosine of each element. When a scalar function f(A) operates on squareMatrix1 (A), the result is calculated by the algorithm: Compute the eigenvalues (λi) and eigenvectors (Vi) of A. squareMatrix1 must be diagonalizable. Also, it cannot have symbolic variables that have not been assigned a value. Form the matrices: Then A = X B X-1 and f(A) = X f(B) X-1. For example, cos(A) = X cos(B) X-1 where: cos(B) =
All computations are performed using floating-point arithmetic. |
In Radian angle mode:
|
|
µ key |
|
|
cos-1(List1) returns a list of the inverse cosines of each element of List1. Note: The result is returned as a degree, gradian or radian angle, according to the current angle mode setting. Note: You can insert this function from the keyboard by typing arccos(...). |
In Degree angle mode:
In Radian angle mode:
|
|
cos-1(squareMatrix1) ⇒ squareMatrix Returns the matrix inverse cosine of squareMatrix1. This is not the same as calculating the inverse cosine of each element. For information about the calculation method, refer to cos(). squareMatrix1 must be diagonalizable. The result always contains floating-point numbers. |
In Radian angle mode and Rectangular Complex Format:
To see the entire result, |
|
Catalog > |
|
|
cosh(Value1) returns the hyperbolic cosine of the argument. cosh(List1) returns a list of the hyperbolic cosines of each element of List1. |
In Degree angle mode:
|
|
cosh(squareMatrix1) ⇒ squareMatrix Returns the matrix hyperbolic cosine of squareMatrix1. This is not the same as calculating the hyperbolic cosine of each element. For information about the calculation method, refer to cos(). squareMatrix1 must be diagonalizable. The result always contains floating-point numbers. |
In Radian angle mode: |
|
Catalog > |
|
|
cosh-1(List1) returns a list of the inverse hyperbolic cosines of each element of List1. Note: You can insert this function from the keyboard by typing arccosh(...). |
new screenshots format (see Z_WriterNotes)
|
|
cosh-1(squareMatrix1) ⇒ squareMatrix Returns the matrix inverse hyperbolic cosine of squareMatrix1. This is not the same as calculating the inverse hyperbolic cosine of each element. For information about the calculation method, refer to cos(). squareMatrix1 must be diagonalizable. The result always contains floating-point numbers. |
In Radian angle mode and In Rectangular Complex Format: To see the entire result, |
|
µ key |
|
|
Returns the cotangent of Value1 or returns a list of the cotangents of all elements in List1. Note: The argument is interpreted as a degree, gradian or radian angle, according to the current angle mode setting. You can use °, G, or r to override the angle mode temporarily. |
In Degree angle mode:
|
|
µ key |
|
|
Returns the angle whose cotangent is Value1 or returns a list containing the inverse cotangents of each element of List1. Note: The result is returned as a degree, gradian or radian angle, according to the current angle mode setting. Note: You can insert this function from the keyboard by typing arccot(...). |
In Degree angle mode:
|
|
Catalog > |
|
|
Returns the hyperbolic cotangent of Value1 or returns a list of the hyperbolic cotangents of all elements of List1. |
|
|
Catalog > |
|
|
Returns the inverse hyperbolic cotangent of Value1 or returns a list containing the inverse hyperbolic cotangents of each element of List1. Note: You can insert this function from the keyboard by typing arccoth(...). |
|
|
Catalog > |
|
|
count(Value1orList1 [,Value2orList2 [,...]]) ⇒ value Returns the accumulated count of all elements in the arguments that evaluate to numeric values. Each argument can be an expression, value, list, or matrix. You can mix data types and use arguments of various dimensions. For a list, matrix, or range of cells, each element is evaluated to determine if it should be included in the count. Within the Lists & Spreadsheet application, you can use a range of cells in place of any argument. Empty (void) elements are ignored. For more information on empty elements, see here.
|
|
|
Catalog > |
|||||||
|
countif(List,Criteria) ⇒ value Returns the accumulated count of all elements in List that meet the specified Criteria. Criteria can be:
Within the Lists & Spreadsheet application, you can use a range of cells in place of List. Empty (void) elements in the list are ignored. For more information on empty elements, see here. |
Counts the number of elements equal to 3.
Counts the number of elements equal to “def.”
Counts 1 and 3.
Counts 3, 5, and 7.
Counts 1, 3, 7, and 9. |
|
Catalog > |
|
|
The first syntax,
The second syntax, Note: See also |
|
|
Catalog > |
|
|
crossP(List1, List2) ⇒ list Returns the cross product of List1 and List2 as a list. List1 and List2 must have equal dimension, and the dimension must be either 2 or 3. |
|
|
crossP(Vector1, Vector2) ⇒ vector Returns a row or column vector (depending on the arguments) that is the cross product of Vector1 and Vector2. Both Vector1 and Vector2 must be row vectors, or both must be column vectors. Both vectors must have equal dimension, and the dimension must be either 2 or 3. |
|
|
µ key |
|
|
Returns the cosecant of Value1 or returns a list containing the cosecants of all elements in List1. |
In Degree angle mode:
|
|
µ key |
|
|
Returns the angle whose cosecant is Value1 or returns a list containing the inverse cosecants of each element of List1. Note: The result is returned as a degree, gradian or radian angle, according to the current angle mode setting. Note: You can insert this function from the keyboard by typing arccsc(...). |
In Degree angle mode:
|
|
Catalog > |
|
|
csch(Value1) ⇒ value csch(List1) ⇒ list
|
|
|
Catalog > |
|
|
Returns the inverse hyperbolic cosecant of Value1 or returns a list containing the inverse hyperbolic cosecants of each element of List1. Note: You can insert this function from the keyboard by typing arccsch(...). |
|
|
Catalog > |
|
|
CubicReg X, Y[, [Freq] [, Category, Include]] Computes the cubic polynomial regression y=a•x3+b•x2+c•x+d on lists X and Y with frequency Freq. A summary of results is stored in the stat.results variable. (See here.) All the lists must have equal dimension except for Include. X and Y are lists of independent and dependent variables. Freq is an optional list of frequency values. Each element in Freq specifies the frequency of occurrence for each corresponding X and Y data point. The default value is 1. All elements must be integers ≥ 0. Category is a list of Include is a list of one or more of the category codes. Only those data items whose category code is included in this list are included in the calculation. For information on the effect of empty elements in a list, see “Empty (Void) Elements,” here. |
|
|
Output variable |
Description |
|
stat.RegEqn |
Regression equation: a•x3+b•x2+c•x+d |
|
stat.a, stat.b, stat.c, stat.d |
Regression coefficients |
|
stat.R2 |
Coefficient of determination |
|
stat.Resid |
Residuals from the regression |
|
stat.XReg |
List of data points in the modified X List actually used in the regression based on restrictions of Freq, Category List, and Include Categories |
|
stat.YReg |
List of data points in the modified Y List actually used in the regression based on restrictions of Freq, Category List, and Include Categories |
|
stat.FreqReg |
List of frequencies corresponding to stat.XReg and stat.YReg |
|
Catalog > |
|
|
cumulativeSum(List1) ⇒ list Returns a list of the cumulative sums of the elements in List1, starting at element 1. |
|
|
cumulativeSum(Matrix1) ⇒ matrix Returns a matrix of the cumulative sums of the elements in Matrix1. Each element is the cumulative sum of the column from top to bottom. An empty (void) element in List1 or Matrix1 produces a void element in the resulting list or matrix. For more information on empty elements, see here. |
|
|
Catalog > |
|
|
Cycle Transfers control immediately to the next iteration of the current loop (For, While, or Loop). Cycle is not allowed outside the three looping structures (For, While, or Loop). Note for entering the example: For instructions on entering multi-line program and function definitions, refer to the Calculator section of your product guidebook. |
Function listing that sums the integers from 1 to 100 skipping 50.
|
|
Catalog > |
|
|
Vector ►Cylind Note: You can insert this operator from the computer keyboard by typing @>Cylind. Displays the row or column vector in cylindrical form [r,∠θ, z]. Vector must have exactly three elements. It can be either a row or a column. |
|