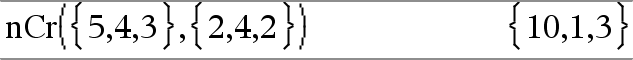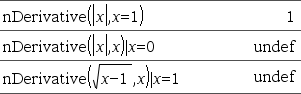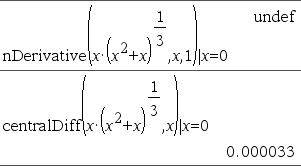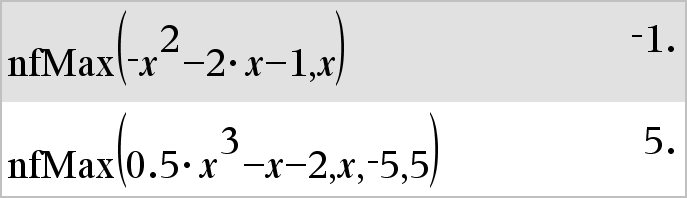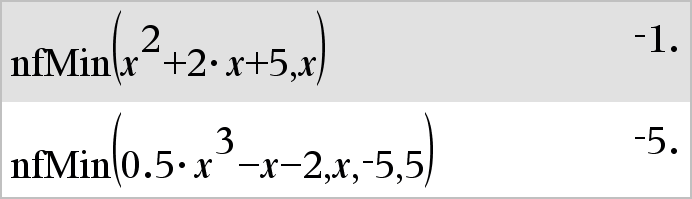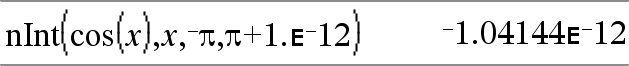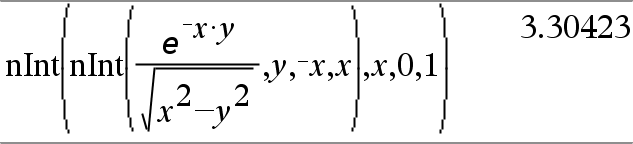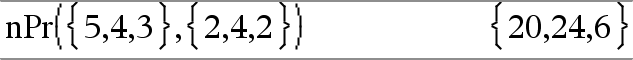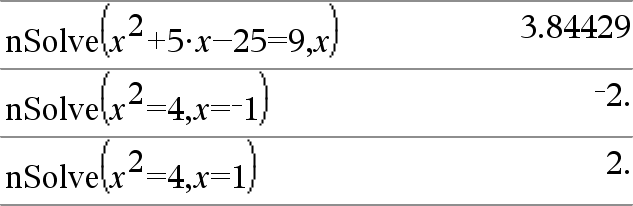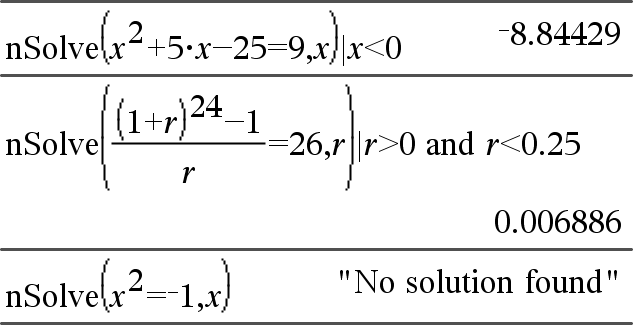|
/= Tasten |
|
|
BoolescherAusdr1 BoolescheListe1 BoolescheMatrix1
Gibt die Negation einer logischen Bei Listen und Matrizen werden die Ergebnisse des Vergleichs der einzelnen Elemente zurückgegeben. |
|
|
Ganzzahl1
Vergleicht zwei reelle ganze Zahlen mit Hilfe einer Sie können die ganzen Zahlen in jeder Basis eingeben. Für eine binäre oder hexadezimale Eingabe ist das Präfix 0b bzw. 0h zu verwenden. Ohne Präfix werden ganze Zahlen als dezimal behandelt (Basis 10). |
|
|
Katalog > |
|
|
nCr(Wert1, Wert2)ÞAusdruck Für ganzzahlige Wert1 und Wert2 mit Wert1 | Wert2 | 0 ist nCr() die Anzahl der Möglichkeiten, Wert1 Elemente aus Wert2 Elementen auszuwählen (auch als Binomialkoeffizient bekannt). nCr(Wert, 0)Þ1 nCr(Wert, negGanzzahl)Þ0 nCr(Wert, posGanzzahl)Þ Wert·(WertN1)... (WertNposGanzzahl+1)/ posGanzzahl!
|
|
|
nCr(Liste1, Liste2)ÞListe Gibt eine Liste von Binomialkoeffizienten auf der Basis der entsprechenden Elementpaare der beiden Listen zurück. Die Argumente müssen Listen gleicher Größe sein. |
|
|
nCr(Matrix1, Matrix2)ÞMatrix Gibt eine Matrix von Binomialkoeffizienten auf der Basis der entsprechenden Elementpaare der beiden Matrizen zurück. Die Argumente müssen Matrizen gleicher Größe sein. |
|
|
Katalog > |
|
|
Gibt die numerische Ableitung zurück, berechnet durch automatische Ableitungsmethoden. Wenn Wert angegeben ist, setzt er jede vorausgegangene Variablenzuweisung oder jede aktuelle „|“ Ersetzung für die Variable außer Kraft. Wenn die Variable Var keinen Zahlenwert enthält, müssen Sie Wert angeben. Ordnung der Ableitung muss 1 oder 2 sein. |
|
|
Hierzu rechts ein Beispiel. Die erste Ableitung von x·(x^2+x)^(1/3) bei x=0 ist gleich 0. Nun ist allerdings die erste Ableitung des Unterausdrucks (x^2+x)^(1/3) bei x=0 nicht definiert. Dieser Wert wird gleichzeitig jedoch verwendet, um die Ableitung des Gesamtausdrucks zu berechnen. Daher meldet nDerivative() das Ergebnis als nicht definiert und zeigt eine Warnmeldung an. Wenn Sie bei der Arbeit auf diese Einschränkung stoßen, prüfen Sie die Lösung grafisch. Ggf. können Sie es auch mit centralDiff() probieren. |
|
|
Katalog > |
|
|
newList(AnzElemente)ÞListe Gibt eine Liste der Dimension AnzElemente zurück. Jedes Element ist Null. |
|
|
Katalog > |
|
|
newMat(AnzZeil, AnzSpalt)ÞMatrix Gibt eine Matrix der Dimension AnzZeil mal AnzSpalt zurück, wobei die Elemente Null sind. |
|
|
Katalog > |
|
|
nfMax(Ausdr, Var)ÞWert nfMax(Ausdr, Var, UntereGrenze)ÞWert nfMax(Ausdr, Var, UntereGrenze, ObereGrenze)ÞWert nfMax(Ausdr, Var) | UntereGrenze{Var{ObereGrenzeÞWert Gibt einen möglichen numerischen Wert der Variablen Var zurück, wobei das lokale Maximum von Ausdr auftritt. Wenn Sie UntereGrenze und ObereGrenze ersetzen, sucht die Funktion in dem geschlossenen Invervall [UntereGrenze,ObereGrenze] für das lokale Maximum. |
|
|
Katalog > |
|
|
nfMin(Ausdr, Var)ÞWert nfMin(Ausdr, Var, UntereGrenze)ÞWert nfMin(Ausdr, Var, UntereGrenze, ObereGrenze)ÞWert nfMin(Ausdr, Var) | UntereGrenze{Var{ObereGrenzeÞWert Gibt einen möglichen numerischen Wert der Variablen Var zurück, wobei das lokale Minimum von Ausdr auftritt. Wenn Sie UntereGrenze und ObereGrenze ersetzen, sucht die Funktion in dem geschlossenen Invervall [UntereGrenze,ObereGrenze] für das lokale Minimum. |
|
|
Katalog > |
|
|
nInt(Ausdr1, Var, Untere, Obere)ÞAusdruck Wenn der Integrand Ausdr1 außer Var keine anderen Variablen enthält und wenn Untere und Obere Konstanten oder positiv ˆ oder negativ ˆ sind, gibt nInt() eine Näherung für ‰(Ausdr1, Var, Untere, Obere) zurück. Diese Näherung ist der gewichtete Durchschnitt von Stichprobenwerten des Integranden im Intervall Untere<Var<Obere. |
|
|
Das Berechnungsziel sind sechs signifikante Stellen. Der angewendete Algorithmus beendet die Weiterberechnung, wenn das Ziel hinreichend erreicht ist oder wenn weitere Stichproben wahrscheinlich zu keiner sinnvollen Verbesserung führen. Wenn es scheint, dass das Berechnungsziel nicht erreicht wurde, wird die Meldung “Zweifelhafte Genauigkeit” angezeigt. |
|
|
Sie können nInt() verschachteln, um mehrere numerische Integrationen durchzuführen. Die Integrationsgrenzen können von außerhalb liegenden Integrationsvariablen abhängen. |
|
|
Katalog > |
|
|
nom(Effektivzins,CpY)ÞWert Finanzfunktion zur Umrechnung des jährlichen Effektivzinssatzes Effektivzins in einen Nominalzinssatz, wobei CpY als Anzahl der Verzinsungsperioden pro Jahr gegeben ist. Effektivzins muss eine reelle Zahl sein und CpY muss eine reelle Zahl > 0 sein. Hinweis: Siehe auch eff(), hier. |
|
|
/= Tasten |
|
|
BoolescherAusd1
BoolescheListe1
BoolescheMatrix1
Gibt die Negation einer logischen Bei Listen und Matrizen werden die Ergebnisse des Vergleichs der einzelnen Elemente zurückgegeben. |
|
|
Ganzzahl1
Vergleicht zwei reelle ganze Zahlen mit Hilfe einer Sie können die ganzen Zahlen in jeder Basis eingeben. Für eine binäre oder hexadezimale Eingabe ist das Präfix 0b bzw. 0h zu verwenden. Ohne Präfix werden ganze Zahlen als dezimal behandelt (Basis 10). |
|
|
Katalog > |
|
|
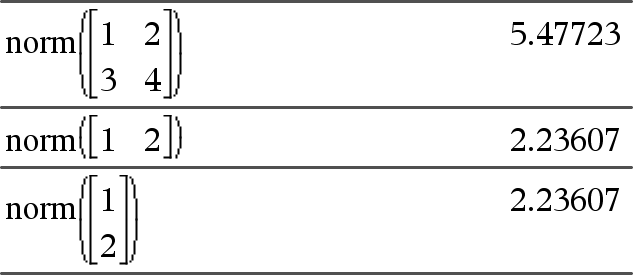
norm(Matrix)ÞAusdruck norm(Vektor)ÞAusdruck Gibt die Frobeniusnorm zurück. |
|
|
Katalog > |
|
|
normCdf(untereGrenze,obereGrenze[,m[,s]])ÞZahl, wenn untereGrenze und obereGrenze Zahlen sind, Liste, wenn untereGrenze und obereGrenze Listen sind Berechnet die Normalverteilungswahrscheinlichkeit zwischen untereGrenze und obereGrenze für die angegebenen m (Standard = 0) und s (Standard = 1).
|
|
|
Katalog > |
|
|
normPdf(XWert[,m[,s]])ÞZahl, wenn XWert eine Zahl ist, Liste, wenn XWert eine Liste ist Berechnet die Wahrscheinlichkeitsdichtefunktion für die Normalverteilung an einem bestimmten XWert für die vorgegebenen m und s. |
|
|
Katalog > |
|
|
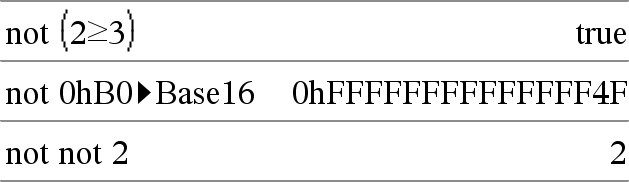
not BoolescherAusdr1ÞBoolescherAusdruck Gibt „wahr“ oder „falsch“ oder eine vereinfachte Form des Arguments zurück. |
|
|
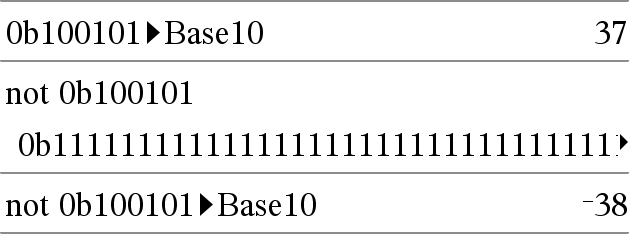
not Ganzzahl1ÞGanzzahl Gibt das Einerkomplement einer reellen ganzen Zahl zurück. Intern wird Ganzzahl1 in eine 32-Bit-Dualzahl mit Vorzeichen umgewandelt. Für das Einerkomplement werden die Werte aller Bits umgekehrt (so dass 0 zu 1 wird und umgekehrt). Die Ergebnisse werden im jeweiligen Basis-Modus angezeigt. Sie können die ganzen Zahlen mit jeder Basis eingeben. Für eine binäre oder hexadezimale Eingabe ist das Präfix 0b bzw. 0h zu verwenden. Ohne Präfix wird die ganze Zahl als dezimal behandelt (Basis 10). Geben Sie eine dezimale ganze Zahl ein, die für eine 64-Bit-Dualform mit Vorzeichen zu groß ist, dann wird eine symmetrische Modulo-Operation ausgeführt, um den Wert in den erforderlichen Bereich zu bringen. Weitere Informationen finden Sie unter 4Base2, hier. |
Im Hex-Modus:
Wichtig: Null, nicht Buchstabe O.
Im Bin-Modus:
Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen. Hinweis: Eine binäre Eingabe kann bis zu 64 Stellen haben (das Präfix 0b wird nicht mitgezählt). Eine hexadezimale Eingabe kann bis zu 16 Stellen aufweisen. |
|
Katalog > |
|
|
nPr(Wert1, Wert2)ÞAusdruck Für ganzzahlige Wert1 und Wert2 mit Wert1 | Wert2 | 0 ist nPr() die Anzahl der Möglichkeiten, Wert1 Elemente unter Berücksichtigung der Reihenfolge aus Wert2 Elementen auszuwählen. nPr(Wert, 0)Þ1 nPr(Wert, negGanzzahl) Þ 1/((Wert+1)·(Wert+2)... (WertNnegGanzzahl)) nPr(Wert, posGanzzahl) Þ Wert·(WertN1)... (WertNposGanzzahl+1) nPr(Wert, keineGanzzahl) |
|
|
nPr(Liste1, Liste2)ÞListe Gibt eine Liste der Permutationen auf der Basis der entsprechenden Elementpaare der beiden Listen zurück. Die Argumente müssen Listen gleicher Größe sein. |
|
|
nPr(Matrix1, Matrix2)ÞMatrix Gibt eine Matrix der Permutationen auf der Basis der entsprechenden Elementpaare der beiden Matrizen zurück. Die Argumente müssen Matrizen gleicher Größe sein. |
|
|
Katalog > |
|
|
npv(Zinssatz,CFO,CFListe[,CFFreq]) Finanzfunktion zur Berechnung des Nettobarwerts; die Summe der Barwerte für die Bar-Zuflüsse und -Abflüsse. Ein positives Ergebnis für npv zeigt eine rentable Investition an. Zinssatz ist der Satz, zu dem die Cash-Flows (der Geldpreis) für einen Zeitraum. CF0 ist der Anfangs-Cash-Flow zum Zeitpunkt 0; dies muss eine reelle Zahl sein. CFListe ist eine Liste der Cash-Flow-Beträge nach dem anfänglichen Cash-Flow CF0. CFFreq ist eine Liste, in der jedes Element die Häufigkeit des Auftretens für einen gruppierten (fortlaufenden) Cash-Flow-Betrag angibt, der das entsprechende Element von CFListeist. Der Standardwert ist 1; wenn Sie Werte eingeben, müssen diese positive Ganzzahlen < 10.000 sein. |
|
|
Katalog > |
|
|
nSolve(Gleichung,Var[=Schätzwert])ÞZahl oder Fehler_String nSolve(Gleichung,Var[=Schätzwert],UntereGrenze) ÞZahl oder Fehler_String nSolve(Gleichung,Var[=Schätzwert],UntereGrenze,ObereGrenze) ÞZahl oder Fehler_String nSolve(Gleichung,Var[=Schätzwert]) | UntereGrenze{Var{ObereGrenze ÞZahl oder Fehler_String Ermittelt iterativ eine reelle numerische Näherungslösung von Gleichung für deren eine Variable. Geben Sie die Variable an als: Variable – oder – Variable = reelle Zahl Beispiel: x ist gültig und x=3 ebenfalls. |
Hinweis: Existieren mehrere Lösungen, können Sie mit Hilfe einer Schätzung eine bestimmte Lösung suchen. |
|
nSolve() versucht entweder einen Punkt zu ermitteln, wo der Unterschied zwischen tatsächlichem und erwartetem Wert Null ist oder zwei relativ nahe Punkte, wo der Restfehler entgegengesetzte Vorzeichen besitzt und nicht zu groß ist. Wenn nSolve() dies nicht mit einer kleinen Anzahl von Versuchen erreichen kann, wird die Zeichenkette “Keine Lösung gefunden” zurückgegeben. |
|