Overview:

At the end of the activity, the last question asked what generalizations about the dimensions of the box can be made from this activity. In this lesson we will use the TI-89 to determine some generalizations to this problem.

In the activity the dimensions used were that of a standard sheet of paper. To begin with some generalizations we will start with a square sheet of paper.

Looking for a Pattern

Assume a sheet of paper that is 6 cm by 6 cm.

What is the size of square to be cut out to maximize the volume of the box created?

Following the steps in the activity the formula for the volume of the box is given by:

V = x(6-2x)(6-2x)

where x is the side of the square cut out.

Determine the maximum volume by graphing the volume equation in Y₁.

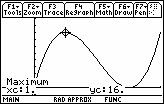
28.2.1 What is the value of x that gives us the maximum volume?

Click here for the answer.

We will also determine the value of x algebraically.

Differentiate the volume formula with respect to x. Press [d] x*(6-2x)*(6-2x) , x ) .

Set the derivative to 0 and solve for x.

1:solve( expression = 0 , x )

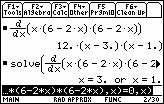
Two values for x should appear. One represents the maximum volume, one the minimum volume. Using the second derivative test we can confirm each. The value for x which maximizes the volume will correspond to the value obtained graphically.

28.2.2 Repeat the above for different dimensions of square paper and examine the ratio of x to the dimensions of the square sheet of paper. What ratio do you notice?

Click here for the answer.

Finding the General Case

We can now use the TI-89 to generalize the ratio using a by a for the size of the paper. The resulting equation for Volume will be:

V = x(a-2x)(a-2x)

Repeat the process of finding the derivative and setting it equal to 0 and solving.

28.2.3 What are your solutions for general ratio?

Click here for the answer.

These should confirm the work you have done previously.

Further Extension

An even further extension is suggested in an article in the November 2002 NCTM publication Mathematics Teacher. The article entitled "Thinking out of the Box ... Problem" suggests keeping the width constant while the length is extended to increasingly larger and larger values. The TI-89 can be used to illustrate that as the limit of the length approaches infinity the ratio of x to the width is ¼.

Click here to read this article.

You will need the Adobe Acrobat Reader^® to access these activities.

Please click on the icon below to download the free Acrobat Reader if you do not have it on your system.