A final related-rate problem, which models a particle moving along a curve, is explored in this lesson.

A particle is moving along the curve y = x³. At a certain instant, the particle is at the point (2, 8) and dx/dt = 5 ft/sec. How fast is the distance s from the particle to the origin changing at that instant?

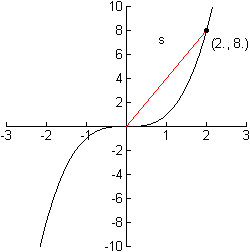
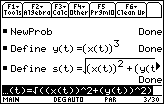
Find the Distance Function s(t)

• Execute the NewProb command
• Define y(t)=(x(t))^3
• Define

Find dy/dt at the Point (2, 8)

We know that dx/dt = 5 at this point. Thus, we need to compute dy/dt with the restrictions that x(t)=2, y(t)=8, and d(x(t),t)=5.

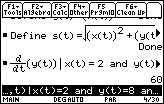
So, dy/dt = 60 ft/sec at the point (2, 8).

Answering the Question

To find out how fast the distance s from the particle to the origin is changing at the specified instant, we need to compute ds/dt with the restrictions that x(t)=2, y(t)=8, dx/dt=5, and dy/dt=60.

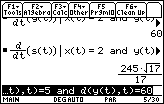
Therefore, the particle is moving away from the origin at