This lesson explores related rates by investigating the positions of the foot and the top of a ladder as it slides down a wall.

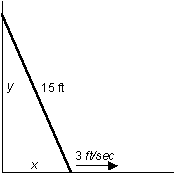
A 15 foot ladder is held against a wall and then released. The foot of the ladder begins to slide along the ground away from the wall at a constant rate of 3 ft/sec. In the diagram below, the distance from the wall to the foot of the ladder is represented by x, and y represents the distance from the ground to the top of the ladder.

Modeling the Position of the Ladder's Foot

Parametric equations can be used to model the position of the foot of the ladder.

Because the foot of the ladder is against the wall at time zero and it is moving at a constant rate of 3 ft/sec, it follows that at time t the foot of the ladder is 3t from the wall. That is,

Because the foot of the ladder does not rise above the ground and its position along the x-axis is given by 3t, the position of the foot of the ladder can be modeled by the parametric equations given below.

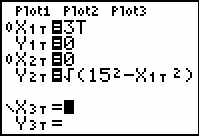
• Set X_1T = 3T
• Set Y_1T = 0

Modeling the Position of the Ladder's Top

Because the wall makes a right angle with the ground, an expression for the position of the ladder's top, y, can by found by using the Pythagorean theorem.

The position of the top of the ladder can be modeled by another set of parametric equations using X_1T for x.

• Set X_2T = 0
• Set
• Set the Graph style of both sets of equations to Animate.

Simulating the Ladder's Motion

To simulate the ladder's motion, display the graphs of the equations simultaneously.

• Select Simultaneous (Simul) in the MODE settings.

• Set the window values to [0, 5, 0.1] x [-1, 16, 1] x [-1, 16, 1]
• Graph the equations.

You should see animated circles that simulate the movement of the top and bottom of the ladder. Notice the rates at which the top and foot of the ladder move.

You can pause the graph by pressing or regraph the equations by selecting ClrDraw from the Draw menu.

16.1.1 Describe the rates at which the top and bottom of the ladder move. Click here for the answer.

Finding the Velocity of the Ladder's Top

Suppose you want to know how fast the top is moving down the wall when the bottom is 5 feet from the wall. The instantaneous velocity of the top of the ladder is the desired value. It is given by the derivative of the function that represents the position of the top.

To find the velocity of the top when the bottom is 5 feet from the wall, evaluate the derivative of y(Y2T) at the value of t that corresponds to x = 5.

Because x = 3t, x = 5 corresponds to . Find the value of when .

• On the Home screen, evaluate nDeriv(Y_2T,T,5/3).

16.1.2 How fast is the top of the ladder moving when the bottom is 5 ft from the wall? Click here for the answer.

Finding the Velocity Function for the Ladder's Top

The velocity of the top of the ladder is a function of time and is the derivative of the position function. Recall that gives the position of the top of the ladder. Because x = 3t, the position of the top of the ladder is given by

16.1.3 Find the function that represents the velocity of the ladder's top. Click here for the answer.

16.1.4 How fast is the top of the ladder moving, in theory, when it hits the ground? Click here for the answer.