In Lesson 9.1 you found average velocities of a falling book over different time intervals. In this lesson you will find the instantaneous velocity of the falling book at t = 0.16.

In Lesson 9.1 the average velocity of the book from t = 0 to t = 0.16 was found to be approximately -0.931 m/s and the average velocity of the book from t = 0.16 to t = 0.28 was found to be approximately -2.183 m/s.

Instantaneous velocity is the velocity of an object at a specific instant, which is the number that would be read from a speedometer at that particular moment. Each of the average velocities previously found could be considered an approximation of the instantaneous velocity at t = 0.16, but neither was exact.

Getting Better Approximations

You can use average velocities to find a series of approximations that will lead to the instantaneous velocity of an object at a given instant by letting the elapsed time between measurements be very small.

9.2.1 Find the average velocities over shorter and shorter intervals near t = 0.16 by using the following data points. Click here for the answer.

Data Points	Average Velocity
(0.16, 0.716) to (0.26, 0.506)
(0.16, 0.716) to (0.22, 0.600)
(0.16, 0.716) to (0.18, 0.681)

9.2.2 Which of the three average velocities is the best approximation to the instantaneous velocity? Why? Click here for the answer.

Fitting a Curve to the Data

The smaller the elapsed time interval, the better the average velocity approximates the instantaneous velocity. The smallest time interval provided by the data near t = 0.16 has length 0.02. However, a regression equation that approximates the data can be used to obtain points even closer to t = 0.16 and those points can then be used to find a better approximation of the book's instantaneous velocity at t = 0.16.

The shape of the data appears to be parabolic, so a quadratic equation should fit the data.

• Open the Stat Calc menu by pressing .
• Choose quadratic regression by selecting 5:QuadReg.
• Complete the command by entering QuadReg L₁, L₂.

Notice the third parameter (Y₁) for the regression command is missing and that the calculator will not store the regression equation in the Y= editor. You will round off the coefficients of the regression equation and manually enter the rounded version in the Y= editor.

Regression command	The regression equation is y -4.503x2 - 0.209x + 0.864

• Enter Y₁ = -4.503X² - 0.209X + 0.864 in the Y= editor.

• Display the regression equation with the scatter plot by pressing .

Using the Regression Equation

The height of the book at t = 0.16 and t = 0.18 can now be approximated by finding Y₁(0.16) and Y₁(0.18). These values can be used to approximate the average velocity of the book between t = 0.16 and t = 0.18 by computing

• Enter the command (Y₁(0.18)-Y₁(0.16))/(0.18-0.16) on the Home screen.
  Y₁ can be pasted to the Home screen by pressing .

The result is a good approximation of the average velocity of -1.75 m/s you found using the table data values over the same interval in Question 9.2.1.

Better Approximations

Points even closer to (0.16, 0.716), which represent shorter time intervals, may be found by using the quadratic function stored in Y₁.

Find the average velocity for the interval from t = 0.16 and t = 0.17 by evaluating

.

Instead of pressing all the keys to enter the above expression, recall and edit the last command on the Home screen.

• Recall the last command by pressing [ENTRY].
  [ENTRY] is above .
• Use the arrow keys to move the cursor until it is on the "8" in Y₁(0.18) and change it to a "7" by pressing .
• Move the cursor to the "8" in the denominator and change it to a "7."
• Evaluate the edited expression by pressing .

Insert and Overwrite Modes When editing expressions on the Home screen, you can insert digits by changing to Insert mode and overwrite digits by switching back to overwrite mode. You can toggle between modes by pressing [INS]. The Insert cursor is a blinking underline character and the overwrite cursor is a blinking solid rectangle.

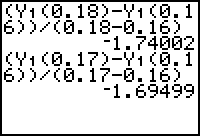
9.2.3 Using the regression equation in Y₁ and the method described above, find the average velocities for the smaller and smaller time intervals shown below.

t = 0.16 to t = 0.161 (elapsed time = 0.001 seconds)

t = 0.16 to t = 0.1601 (elapsed time = 0.0001 seconds)

t = 0.16 to t = 0.16001 (elapsed time = 0.00001 seconds)

Click here for the answer.

Finding Instantaneous Velocity

As the elapsed time approaches zero, the average velocities approach a limiting value. This limit is the instantaneous velocity and it can be found by letting h represent the elapsed time and evaluating

, or equivalently

The three average velocities found in Question 9.2.3 could also be found by letting h = 0.001, 0.0001, and 0.00001

and evaluating .

Evaluating for smaller and smaller values of h gives an approximation for

, the instantaneous velocity at t = 0.16.

Finding the Exact Value of the Limit

In order to find the exact value of the limit, the expression must first be simplified, as shown below. Recall that Y₁ = -4.503x² - 0.209x + 0.864.

The limit of the last expression as h approaches 0 is -4.503(0.32) - 0.209 = -1.64996, so the instantaneous velocity at t = 0.16 is approximately -1.64996 m/s.

Illustrating Instantaneous Velocity

Just as the slope of the line that connects two points on the graph of height vs. time represents the average velocity between the two points, a special line is associated with the instantaneous velocity: the tangent line to the curve at the desired point.

The slope of the tangent line to a curve at a given point is defined the same way as instantaneous velocity.

Definition of a Tangent Line to a Curve

The tangent line to the graph of f at the point (a, f(a)) is the line through (a, f(a)) with slope

provided the limit exists.

Drawing a Tangent Line

A tangent line to a curve at a given point can be drawn with the Tangent feature, which is found in the Draw menu.

• Return to the Graph screen by pressing .
• Open the Draw menu by pressing [DRAW].

• Select 5:Tangent(.

• Enter the x-coordinate of the point of tangency, 0.16, and press .

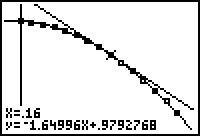
Enter the x-value of the desired point.	Instantaneous velocity illustrated

The equation at the bottom of the last screen, y = -1.64996x + 0.9792768 , is the equation of the line tangent to the curve at the point t = 0.16. Notice that the slope of this line, -1.64996, is equal to the instantaneous velocity found earlier by evaluating the limit

The Tangent Command from the Home Screen The Tangent command can be used from the Graph screen, as described above, or from the Home screen. Display the Home screen by pressing [QUIT]. Display the DRAW menu by pressing [DRAW]. Paste "Tangent(" to the Home screen by selecting 5:Tangent(. The syntax for the command is Tangent(expression,value). Complete the command by entering the desired expression and value of x. Y1 can be used to denote the expression and the value of x can be given as an expression.