This lesson exlores the relationship between antiderivatives and indefinite integrals and discusses families of curves.

Mathematics can be discovered using the TI-89, as illustrated in Module 2 and Module 10. There is a sense of ownership and interest that is acquired with inductive learning. Review the discovery-learning process which was described in Module 2 and Module 10 and is shown below.

• Explore several related examples
• Describe verbally the pattern of the results
• Predict the result
• Confirm the prediction
• Extend the types of examples explored
• Generalize

Defining Indefinite Integrals

Recall that an antiderivative of a function f is a function F whose derivative is .

The Fundamental theorem gives a relationship between an antiderivative F and the function f.

, where F'(x) = f(x) and a is any constant.

A modified notation is used to signify the antiderivatives of f. The new notation is called an indefinite integral and the antiderivatives of f are written as

Definite vs. Indefinite Integrals There are no limits of integration in an indefinite integral. A definite integral represents a number when the lower and upper limits are constants. The indefinite integral represents a family of functions whose derivatives are f. The difference between any two functions in the family is a constant.

Using the Integral Key

The integral key, which is used to find definite integrals, can also be used to find indefinite integrals by simply omitting the limits of integration.

Indefinite Integral Syntax The syntax for finding an indefinite integral is .

Exploring

Examine the antiderivative of each of the following functions that have the form xⁿ and look for a pattern that will lead you to a general rule for finding .

• Evaluate
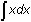
• Evaluate
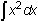
• Evaluate

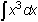
Notice that the arbitrary constant C is not part of the result given by the TI-89.

Adding a Constant to The Indefinite Integral Syntax The syntax for adding the constant c to an indefinite integral is

Describing the Pattern and Predicting

18.1.1 Describe the pattern you found when evaluating the indefinite integrals above and use it to predict .
Click here for the answer.

18.1.2 Confirm your prediction of on your TI-89.
Click here for the answer.

Extending the Examples

Extend the exploration of examples by predicting the following indefinite integrals.

• Evaluate
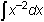
• Evaluate

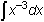
18.1.3 Confirm your predictions by entering the integrals on your TI-89.
Click here for the answer.

Generalizing the Pattern

18.1.4 Predict a general rule for and confirm it by entering the integral on your TI-89.
Click here for the answer.

Checking Indefinite Integrals

Because you can check each indefinite integral's result by finding the derivative of the result. For example, can be verified by taking the derivative of the result: . Because the result of the differentiation is the original function, the integration is confirmed.

The Generalized Rule

The generalized version of this rule is , where and C is a constant. Recall that the derivative of a constant is 0, so for any constant C.

Illustrating

The indefinite integral may be illustrated by graphing the family of curves that are represented by for different values of C. For example, corresponds to . Letting C take the values -240, -200, -160, -120, -80, -40, 0, 40, 80, the family of curves is shown below in a [0, 50] x [-50, 100] window where the particular curve associated with C = 0 is darker.

Each curve in the family can be obtained by choosing a different value of C and vertically translating the curve corresponding to C = 0.