This lesson explores the relationship between antiderivatives and indefinite integrals and discusses families of curves. You will also investigate finding antiderivatives graphically and analytically.

Defining Indefinite Integrals

Recall that an antiderivative of a function f is a function F whose derivative is f, that is,

.

The Fundamental Theorem of Calculus gives another relationship between an antiderivative F and the function f:

If a is a constant, then -F(a) is a constant and we call it C, and the above can be written as

.

A modified notation, , is used to represent all the antiderivatives of f. The new notation is called an indefinite integral. So, the indefinite integral is defined as

Definite vs. Indefinite Integrals A definite integral represents a number when the lower and upper limits are constants. An indefinite integral represents a family of functions all of whose derivatives are equal to f. The difference between any two functions in the family is a constant. There are no limits of integration in an indefinite integral.

Exploring Graphically

Suppose you are to find an antiderivative of f(x) = x². The Fundamental Theorem of Calculus says that by varying the value of a, will produce a whole family of antiderivatives, so explore the graph of for a = 0 and see if you can determine an antiderivative of x². Letting a = 0 will produce one antiderivative of the family of antiderivatives.

• Enter Y₁ = fnInt(T²,T,0,X).
• Graph Y₁ in a [-5, 5, 1] x [-5, 5, 1] viewing window.

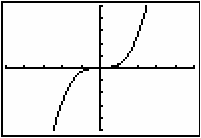
This antiderivative looks like f(x) = x³. However, graphing Y₂ = X^3 together with the antiderivative in Y₁ shows they are not quite the same.

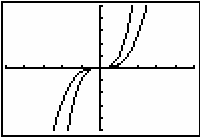
The antiderivative in the graph is actually . Define Y₂ as X^3/3 to provide graphical support that is an antiderivative of f(x) = x².

20.1.1 Graph an antiderivative of f(x) = x³ and find an equation for one antiderivative. Support your work graphically.

Click here for the answer.

Checking Indefinite Integrals Analytically

Because you can check an indefinite integral by taking the derivative of the result. For example, the fact that can be verified by taking the derivative of the result:

.

The Power Rule for Indefinite Integrals

The generalized version for antidifferentiation where is

, where C is an arbitrary constant.

Illustrating

The indefinite integral may be illustrated by graphing the family of curves that are represented by for different values of C. For example, corresponds to . Letting C take the values -240, -200, -160, -120, -80, -40, 0, 40, 80, the family of curves is shown below in a [0, 50,10] x [-50, 100,10] window, where the particular curve associated with C = 0 is the darker curve.

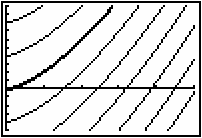
Each curve in the family can be obtained by choosing a different value of C and vertically translating the curve corresponding to C = 0.