Sx1, Sx2
=
樣本標準差的自由度 df 分別為 n1N1 和 n2N1。
F
=
F-statistic = 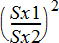
df(x, n1N1, n2N1)
=
Fpdf( ) 自由度為 df, n1N1 和 n2N1
p
=
回報的 p 值
以下是可以在 [序列 & 試算表] 應用程式中使用的假設檢定。 如需關於這些函數的詳細資訊,請參閱《TI‑Nspire™ 參考指南》。
統計檢定的某些精靈會顯示 [繪製] 核取方塊。 該核取方塊預設為已選取。 選取該方塊可在頁面上建立一個 [數據 & 統計] 工作區域,並在該工作區域繪製計算結果圖表。
執行單個不明母群體平均值 m 的假設檢定,且母群體標準差 s 為已知。 它根據下列其中一個對立假設,檢定虛無假設 H0: m=m0。
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
此檢定使用於常態分布的大型母群體。 必須已知標準差。
此檢定有助於在您清楚母群體的真實差時,用來判斷樣本平均值與母群體平均值之間的殘差是否具有統計上的顯著性。
執行單個不明母群體平均值 m 的假設檢定,且母群體標準差 s 不明。 它根據下列其中一個對立假設,檢定虛無假設 H0: m=m0。
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
此檢定類似於 z 檢定,但會在母群體較小且為常態分布的情況下使用。 此檢定比 z 檢定更常使用,因為在統計學中,小型樣本母群體比大型樣本母群體更常見。
此檢定有助於用來判斷兩個常態分布的母群體平均值是否相等,或當您未知母群體標準差時,需判斷樣本平均值與母群體平均值的殘差是否具顯著性。
在母群體標準差(s1 和 s2)皆為已知時,以獨立樣本為基礎,檢定兩個母群體的平均值等式(m1 和 m2)。 它根據下列其中一個對立假設,檢定虛無假設 H0: m1=m2。
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
在母群體標準差(s1 或 s2)皆為未知時,以獨立樣本為基礎,檢定兩個母群體的平均值等式 (m1 和 m2)。 它根據下列其中一個對立假設,檢定虛無假設 H0: m1=m2。
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
計算未知成功比例 (prop) 的檢定。 它需要在每一個樣本 x 中輸入成功計數,以及在每一個樣本 n 中輸入觀測計數。 1‑ 比例 z 檢定根據下列其中一個對立假設,檢定虛無假設 H0: prop=p0。
| • | Ha: propƒp0 |
| • | Ha: prop<p0 |
| • | Ha: prop>p0 |
此檢定有助於用來判斷樣本中所見的成功機率與母群體的成功機率是否具有顯著性的殘差,或該顯著性是否由於抽樣錯誤、差或其他因子所造成。
計算檢定以比較來自兩個母群體的成功比例(p1 和 p2)。 它需要在每一個樣本(x1和x2)中輸入成功計數,以及在每一個樣本(n1 和 n2)中輸入觀測計數。 2‑比例 z 檢定根據下列其中一個對立假設,檢定虛無假設 H0: p1=p2(使用合併樣本比例 Ç)。
| • | Ha: p1ƒp2 |
| • | Ha: p1<p2 |
| • | Ha: p1>p2 |
此檢定有助於用來判斷兩個樣本中的成功機率是否相等。
執行檢定,確認資料樣本的確來自符合特定分布的母群體。 例如,c2 GOF 可確認樣本資料是否來自常態分布。
計算卡方檢定,用於指定的觀察矩陣中計數的雙向交叉表之關聯性。 雙向交叉表的虛無假設 H0 為:列變數與欄變數之間不存在關聯性。 對立假設為:變數是相關的。
會計算 F‑ 檢定,以比較兩個常態母群體的標準差(s1 和 s2)。 母群體的平均值與標準差均為未知。 2‑ 樣本 F檢定使用樣本變異數比例 Sx12/Sx22,會根據下列其中一個對立假設,檢定虛無假設 H0: s1=s2。
| • | Ha: s1ƒs2 |
| • | Ha: s1<s2 |
| • | Ha: s1>s2 |
下列是2‑樣本 F檢定的定義。
|
Sx1, Sx2 |
= |
樣本標準差的自由度 df 分別為 n1N1 和 n2N1。 |
|
|
|
F-statistic = |
|
df(x, n1N1, n2N1) |
= |
Fpdf( ) 自由度為 df, n1N1 和 n2N1 |
|
p |
= |
回報的 p 值 |
用於對立假設 s1 > s2 的2‑樣本F檢定。
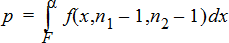
用於對立假設 s1 < s2 的2‑樣本F檢定。
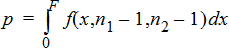
用於對立假設 s1ƒs2 的2‑樣本F檢定。 極限必須滿足以下所列:
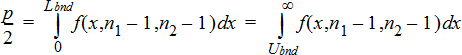
其中: [Lbnd,Ubnd]=下限與上限
F‑ statistic 為產生最小積分的界限。 系統會選取剩餘的界限來得到前一個積分的等式關係。
計算給定資料的線性迴歸、b 斜率值上的 t 檢定,以及 y=a+bx 方程式的 r 相關係數。 它根據下列其中一個對立假設,檢定虛無假設 H0: b=0 (等同於 r=0)。
| • | Ha: bƒ0 and rƒ0 |
| • | Ha: b<0 and r<0 |
| • | Ha: b>0 and r>0 |
在給定資料上計算線性迴歸,並提供線性的 F 檢定統計量。
如需詳細資訊,請參考 TI‑Nspire™ 參考指南。
計算單因子變異數分析,比較 2 至 20 個母群體的平均值。 比較這些平均值的 ANOVA 程序在相同樣本資料中進行變異分析。 會根據下列對立假設 Ha 檢定虛無假設 H0: m1=m2=...=mk:並非所有的 m1...mk 都相等。
ANOVA 檢定方法,可判斷群組間的殘差與各群組內發生的殘差之間是否具有顯著性。
此檢定有助於判斷來自樣本對樣本間的資料變異,是否在統計上有資料集本身變異之外的某因子具有顯著性的影響。 例如,貨運公司的紙箱採購人員要評估三家不同的紙箱製造商。 他會從三家供應商取得樣品紙箱。 ANOVA 可協助判斷各樣品群組間的差異與各樣品群組內的差異之間,是否具有顯著性。
計算雙因子變異數分析,比較 2 至 20 個母群體的平均值。 stat.results 變數儲存結果摘要。
雙向 ANOVA 變異數分析會檢查兩個自變數的影響,並協助判斷這些自變數是否與因變數進行互動。 (也就是說,如果兩個自變數之間有互動,其結合的影響可能會大於或小於單獨自變數的影響。)
此檢定有助於評估類似於 ANOVA 分析的差異,但是會增加對其他潛在影響的考量。 若繼續進行 ANOVA 紙箱範例,雙向 ANOVA 可以檢查紙箱材料在可見差異上的影響。
假設檢定的大部份推論統計編輯器會顯示提示,以選取三個對立假設的其中一個。
| • | 第一個是ƒ對立假設,例如z 檢定的 mƒm0。 |
| • | 第二個是 <對立假設,例如2‑樣本 t 檢定的m1<m2。 |
| • | 第三個是 > 對立假設,例如 2‑ 比例 z 檢定的 p1>p2 。 |
若要選取一個對立假設,請將游標移到適當的對立假設,然後按 Enter。
合併(僅 2‑樣本 t 檢定和2‑樣本 t 區間 )會指定是否要合併變異數以供計算使用。
| • | 如果不要合併變異數,請選取[否]。 母群體變異數可以不相等。 |
| • | 如果要合併變異數,請選取[是]。 假設母群體變異數相等。 |
若要選取 [合併] 選項,請從下拉式方塊選取 [是]。