菜单可让您从下面介绍的计算中选择。 有关更多相关信息,请参阅 TI‑Nspire™ 参考 指南。
单变量统计 (OneVar)
用一个测得的变量分析数据。 您可以指定一个可选的频率列表。 使用此分析方法返回的统计数据如下:
双变量统计 (TwoVar)
分析成对数据。 列表 1 是自变量。 列表 2 是因变量。 您可以指定一个可选的频率列表。 使用此分析方法返回的统计数据如下:
对于每个列表:
|
•
|
样本标准差,sx = sn-1x 或 sy = sn-1y |
|
•
|
总体标准差,sx = snx 或 sy = sny |
|
•
|
方差的和,SSx = G(x Nx)2 或 SSy = G(y Ny)2 |
其它数据:
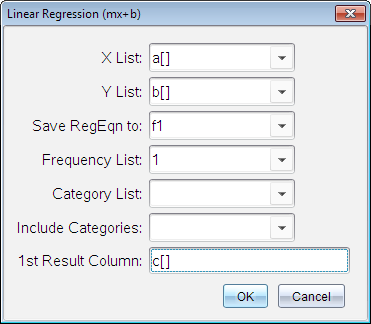
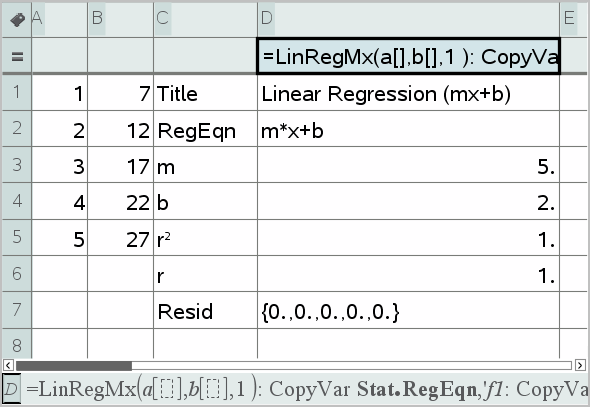
线性回归 (mx+b) (LinRegMx)
使用最小二乘拟合将模型方程式 y=ax+b 与数据拟合。 它显示 m(斜率)和 b (y‑轴截距)的值。
线性回归 (a+bx) (LinRegBx)
使用最小二乘拟合将模型方程式 y=a+bx 与数据拟合。 它显示 a(y‑轴截距)、b (斜率)、r2 以及 r。
中位线 (MedMed)
使用中位线(耐抗线)方法将模型方程式 y=mx+b 与数据拟合,计算摘要点 x1、y1、x2、y2、x3 和 y3。 “中‑位 线 显示 m (斜率)和 b (y‑轴截距)的值。
二次回归 (QuadReg)
将二次多项式 y=ax2+bx+c 与数据拟合。 它显示 a、b、c 和 R2 的值。 对于三个数据点,该方程式为多项式拟合;对于四个或四个以上数据点,该方程式为多项式回归。 需要至少三个数据点。
三次回归 (CubicReg)
将三次多项式 y=ax3+bx2+cx+d 与数据拟合。 它显示 a、b、c、d 和 R2 的值。 对于四个数据点,该方程式为多项式拟合;对于五个或五个以上数据点,该方程式为多项式回归。 需要至少四个点。
四次回归 (QuartReg)
将四次多项式 y=ax4+bx3+cx2+dx+e 与数据拟合。 它显示 a、b、c、d、e 和 R2 的值。 对于五个数据点,该方程式为多项式拟合;对于六个或六个以上数据点,该方程式为多项式回归。 需要至少五个点。
幂回归 (PowerReg)
使用变换值 ln(x) 和 ln(y) 上的最小二乘拟合将模型方程式 y=axb 与数据拟合。 它显示 a、b、r2 和 r 的值。
指数回归 (ExpReg)
使用变换值 x 和 ln(y) 上的最小二乘拟合将模型方程式 y=abx 与数据拟合。 它显示 a、b、r2 和 r 的值。
对数回归 (LogReg)
使用变换值 x 和 ln(y) 上的最小二乘拟合将模型方程式 y=a+b ln(x) 与数据拟合。 它显示 a、b、r2 和 r 的值。
正弦回归 (SinReg)
使用迭代最小二乘拟合将模型方程式 y=a sin(bx+c)+d 与数据拟合。 它显示 a、b、c 和 d 的值。 需要至少四个点。 每个周期需要至少两个数据点才能避免混杂频数估算。
注: 不论“弧度/度数”模式设置如何,SinReg 的输出始终为弧度。
逻辑回归 (d=0) (Logistic)
使用迭代最小二乘拟合将模型方程式 y=c/(1+a*e⁻bx) 与数据拟合。 它显示 a、b 和 c 的值。
逻辑回归 (dƒ0) (LogisticD)
使用迭代最小二乘拟合将模型方程式 y=c(1+a*e(⁻bx))+d 与数据拟合。 它显示 a、b、c 和 d 的值。
多元线性回归 (MultReg)
计算列表 X1、X2、…、X10 中列表 Y 的多元线性回归。
 进行统计计算
进行统计计算