Sx1、 Sx2
=
样本的标准差的自由度 df 分别是 n1N1 和 n2N1。
F
=
F-statistic = 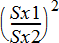
df(x, n1N1, n2N1)
=
Fpdf( ) 的自由度 df 为 n1N1 和 n2N1
p
=
报告的 p 值
“列表与电子表格”应用程序可提供假设检验。 有关这些函数的详细信息,请参阅 TI‑Nspire™ 参考指南。
统计检验的一些向导会显示绘图复选框。 默认情况下选中该复选框。 选中该框可在页面中创建“数据与统计”工作区并绘制该工作区中的结果。
在总体标准差 s 已知的情况下,执行单个未知总体平均值 m 的假设检验。 它对照以下备选之一检验零假设 H0: m=m0 。
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
此检验用于正态分布的大型总体。 标准差必须为已知。
此测试用于在知道总体的真实偏差时确定样本平均值和总体平均值之差是否有统计显著性。
在总体标准差 s 未知的情况下,执行单个未知总体平均值 m 的假设检验。 它对照以下备选之一检验零假设 H0: m=m0 。
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
此检验与 z 检验类似,但用在总体较小并且为正态分布时。 此检验比 z 检验更常用,因为统计中小型样本总体比大型总体更常见。
此检验用于确定两个正态分布总体平均值是否相等,或用于确定样本平均值是否与总体平均值有显著差异(总体标准差未知)。
在两个总体标准差(s1 和 s2)已知的情况下,检验基于独立样本的两个总体平均值(m1 和 m2)是否相等。 零假设 H0: m1=m2 对照以下备选之一进行检验。
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
在两个总体标准差(s1 或 s2)已知的情况下,检验基于独立样本的两个总体平均值(m1 和 m2)是否相等。 零假设 H0: m1=m2 对照以下备选之一进行检验。
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
计算未知成功比例 (prop) 的检验。 它将样本 x 中的成功计数和样本 n 中的观察计数作为输入。 ‑单比例 z 检验 对照以下备选之一检验零假设 H0: prop=p0。
| • | Ha: propƒp0 |
| • | Ha: prop<p0 |
| • | Ha: prop>p0 |
此检验用于确定样本中看到的成功概率与总体概率有无显著差异,或这种差异是否由于抽样误差、偏差或其它因素导致。
计算检验以比较两个总体的成功比例(p1 和 p2)。 它将每个样本中的成功计数(x1 和 x2)和每个样本中的观察计数(n1 和 n2)作为输入。 双‑比例 z 检验 对照以下备选之一检验零假设 H0: p1=p2 (使用合并的样本比例 Ç)。
| • | Ha: p1ƒp2 |
| • | Ha: p1<p2 |
| • | Ha: p1>p2 |
此检验用于确定两个样本中出现的成功概率是否相等。
执行检验以确认样本数据来自于符合指定分布的总体。 例如,c2 GOF 可确认样本数据来自正态分布。
计算指定观察到的矩阵中计数双向表格关联性的卡方检验。 双向表格的零假设 H0 为:行变量与列变量之间没有关联性。 备选假设为:这些变量相关。
计算 F‑ 检验以比较来那个正态总体标准差 (s1 和 s2)。 总体平均值和标准差均未知。 双‑样本 F 检验(使用样本方差比率 Sx12/Sx22)对照以下备选之一检验零假设 H0: s1=s2。
| • | Ha: s1ƒs2 |
| • | Ha: s1<s2 |
| • | Ha: s1>s2 |
下面是双‑样本 F 检验的定义。
|
Sx1、 Sx2 |
= |
样本的标准差的自由度 df 分别是 n1N1 和 n2N1。 |
|
|
|
F-statistic = |
|
df(x, n1N1, n2N1) |
= |
Fpdf( ) 的自由度 df 为 n1N1 和 n2N1 |
|
p |
= |
报告的 p 值 |
双‑样本 F 检验用于备选假设 s1 > s2。
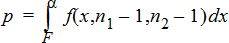
双‑样本 F 检验用于备选假设 s1 < s2。
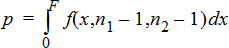
双‑样本 F 检验用于备选假设 s1ƒs2。 极限必须满足以下条件:
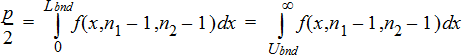
其中: [Lbnd,Ubnd]=下限和上限
F‑ 统计用作边界以生成最小积分。 选择另一个边界以存档前导积分的相等关系。
计算指定数据的线性回归并对方程式 y=a+bx 的斜率值 b 和相关系数 r 执行 t 检验。 它对照以下备选之一检验零假设 H0: b=0(等同于 r=0)。
| • | Ha: bƒ0 和 rƒ0 |
| • | Ha: b<0 和 r<0 |
| • | Ha: b>0 和 r>0 |
计算指定数据的线性回归,并提供线性的 F 检验统计量。
有关更多相关信息,请参阅 TI‑Nspire™ 参考指南。
计算单因素的方差分析以比较两个到 20 个总体的平均值。 用于比较这些平均值的 ANOVA 过程涉及样本数据的方差分析。 零假设 H0: m1=m2=...=mk 对照备选 Ha:(并非所有 m1...mk 均相等)进行检验。
ANOVA 检验是比较每组内出现的差异以确定各组之间是否有显著差异的一种方法。
此检验用于确定样本之间的数据差异是否显示出除数据集本身内差异以外的其它因素对统计显著性的影响。 例如,运输公司的箱子采购员想要评估三个不同的箱子生产商。 他将从所有三个供应商获得样本。 通过在各样本组内比较差异,ANOVA 可帮助他确定各样本组之间的差异是否显著。
计算双因素的方差分析以比较两个到 20 个总体的平均值。 结果摘要存储在 stat.results 变量中。
双因素 ANOVA 方差分析检查两个自变量的影响,以便确定其是否相互作用进而影响因变量。 (换句话说,如果两个自变量相互作用,其组合影响可能大于或小于两个自变量单独作用并相加的影响。)
此检验用于评估类似 ANOVA 分析的差异,但增加了另一个潜在影响。 继续以 ANOVA 箱子为例,双因素 ANOVA 可能会检查箱子材料差异的影响。
大多数假设检验的推断统计编辑器会提示您选择以下三种备选假设之一。
| • | 第一种是 ƒ 备选假设,例如 z 检验 的 mƒm0。 |
| • | 第二种是<备选假设,例如 双‑样本 t 检验 的 m1<m2。 |
| • | 第三种是>备选假设,例如 双‑比例 z 检验 的 p1>p2。 |
要选择备选假设,请将光标移动到相应的备选项,然后按 Enter。
合并(仅限 双‑样本 t 检验 和 双‑样本 t 区间)指定计算是否合并方差。
| • | 如果不想合并方差,请选择 否。 总体方差可以不相等。 |
| • | 如果要合并方差,请选择 是。 此时假设总体方差相等。 |
要选择 合并选项,请从下拉框中选择“是”。