Tilastolaskennan avulla voit analysoida dataa. Seuraavassa esimerkissä lineaarista regressiomallia y=mx+b sovitetaan kahteen listaan sarakkeissa A ja B.

1.

Valitse Tilastot-valikosta Tilastolaskenta> Lineaarinen regressio (mx+b) regressiomallin valitsemiseksi.

Lineaarinen regressio (mx+b) -valintaikkuna avautuu.

2.

Näppäile a[] sarakkeeksi X-listalle.

3.

Näppäile b[] sarakkeeksi Y-listalle.

4.

Jos haluat tallentaa regressioyhtälön johonkin tiettyyn muuttujaan, korvaa teksti Tallenna RegYht nimellä muuttujan nimellä.

5.

Näppäile c[] sarakkeeksi 1. tulokselle.

6.

Napsauta OK.

Listat & taulukot lisää kaksi saraketta: toinen sisältää vastausten nimet ja toinen niitä vastaavat arvot.

Huomaa: Tulokset on linkitetty lähdedataan. Jos esimerkiksi vaihdat arvon sarakkeessa A, regressioyhtälö päivitetään automaattisesti.

 

Listat & taulukot tallentaa tilastolaskujen vastaukset käyttäen muuttujaryhmän nimeä, joka on muotoa stat.nnn, jossa nnn on vastauksen nimi (esimerkiksi stat.RegEqn ja stat.Resid). Vakionimien käyttäminen muuttujien niminä helpottaa tilastomuuttujien myöhempää tunnistamista ja käyttöä. Jos haluat käyttää mukautettua muuttujaryhmää vakionimen sijaan, voit muokata sarakekaavan solussa olevaa kaavaa.

Voit käyttää esimerkiksi seuraavanlaista kaavaa tulosten tallentamiseksi muuttujaryhmään MystatsB.

=LinRegMx(a[],b[],1 ): CopyVar Stat., MystatsB.

Voit myöhemmin tarkastella vastauksia syöttämällä seuraavan lausekkeen  Laskin-sovellukseen tai johonkin toiseen Listat & taulukot -sovelluksen sarakkeeseen:

MystatsB.results

 

Tilastolaskenta-valikosta voit valita seuraavassa kuvatut laskutoimitukset. Katso lisätietoja TI‑Nspire™   -käyttöoppaasta.

Yhden muuttujan tilastot (OneVar)

Analysoi dataa yhdellä mitatulla muuttujalla. Voit määrittää valinnaisen frekvenssilistan. Tällä analyysimenetelmällä saadaan seuraavat tilastotiedot:

•

Otoksen keskiarvo, x

•

Datan summa, Gx

•

Datan neliösumma, Gx2

•

Otoksen keskihajonta, sx

•

Perusjoukon keskihajonta, sx

•

Otoksen koko, n

•

X‑min

•

Ensimmäinen neljännes, Q1

•

Mediaani

•

Kolmas neljännes, Q3

•

X‑max

•

Toiseen potenssiin korotettujen hajontojen summa, SSx = G(x Nx)2

Kahden muuttujan tilastot (TwoVar)

Analysoi datapareja. Lista 1 on riippumaton muuttuja. Lista 2 on riippuva muuttuja. Voit määrittää valinnaisen frekvenssilistan. Tällä analyysimenetelmällä saadaan seuraavat tilastotiedot:

Jokaisesta listasta:

•

Otoksen keskiarvo, x tai y

•

Datan summa, Gx tai Gy

•

Datan neliösumma, Gx2 tai Gy2

•

Otoksen keskihajonta, sx = sn-1x tai sy = sn-1y

•

Perusjoukon keskihajonta, sx = snx tai sy = sny

•

X‑min tai Y-min

•

Ensimmäinen neljännes, Q1X tai Q1Y

•

Mediaani

•

Kolmas neljännes, Q3X tai Q3Y

•

X‑max tai Y-max

•

Toiseen potenssiin korotettujen hajontojen summa, SSx = G(x Nx2 tai SSy = G(y Ny)2

Lisätiedot:

•

Jokaisen datasarjan otoksen koko, n

•

Gxy

•

Korrelaatiokerroin, R.

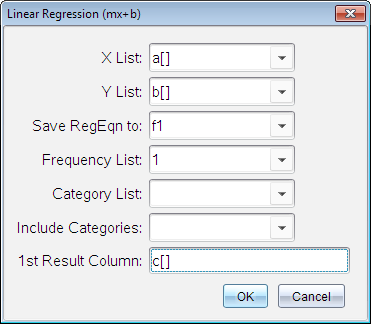
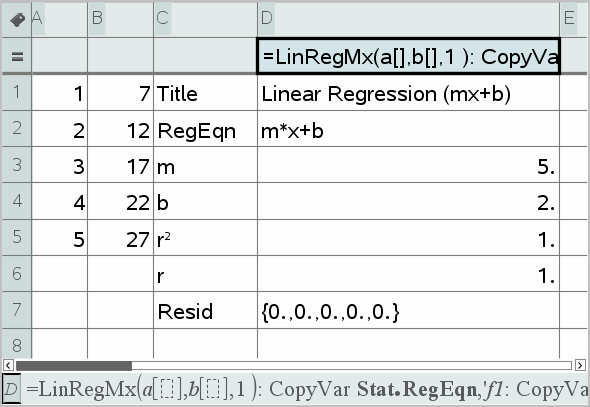
Lineaarinen regressio (mx+b) (LinRegMx)

Sijoittaa yhtälön y=ax+b tietoihin käyttäen pienimmän neliösumman menetelmää. Se näyttää m:n (kulmakerroin) ja b:n (y‑-leikkaus) arvot.

Lineaarinen regressio (a+bx) (LinRegBx)

Sijoittaa yhtälön y=a+bx tietoihin käyttäen pienimmän neliösumman menetelmää. Se näyttää a:n (y‑-leikkaus), b:n (kulmakerroin), r2:n ja r:n arvot.

Mediaani-mediaani-suora (MedMed)

Sovittaa dataan malliyhtälöä y=mx+b käyttäen mediaani-mediaani-suoran (resistentti suora) menetelmää ja laskien yhteenvetopisteet x1, y1, x2, y2, x3 ja y3. Mediaani‑mediaani- suora näyttää m:n (kulmakerroin) ja b:n (y‑-leikkaus) arvot.

2. asteen regressio (QuadReg)

Sovittaa toisen asteen polynomin y=ax2+bx+c tietoihin. Se näyttää a:n, b:n, c:n ja R2:n arvot. Kolmelle pisteelle yhtälö on polynomisovitus; jos pisteitä on neljä tai enemmän, kyseessä on polynomiregressio. Vähintään kolme tietopistettä tarvitaan.

3. asteen regressio (CubicReg)

Sovittaa kolmannen asteen polynomin y=ax3+bx2+cx+d tietoihin. Se näyttää a:n, b:n, c:n, d:n ja R2:n arvot. Neljän pisteen tapauksessa yhtälö on polynomin sovitus; jos pisteitä on viisi tai enemmän, kyseessä on polynominregressio. Vähintään neljä pistettä tarvitaan.

4. asteen regressio (QuartReg)

Sovittaa dataan neljännen asteen polynomifunktion y=ax4+bx3+cx2+dx+e dataan. Se näyttää a:n, b:n, c:n, d:n, e:n ja R2:n. Viidessä datapisteessä yhtälö on polynominen. Jos pisteitä on kuusi tai enemmän, se on polynomiregressio. Vähintään viisi pistettä vaaditaan.

Potenssiregressio (PowerReg)

Sovittaa malliyhtälön y=axb annettuihin arvoihin käyttäen pienimmän neliösumman menetelmää muunnettuihin arvoihin ln(x) ja ln(y). Se näyttää a:n, b:n, r2:n ja r:n arvot.

Eksponentiaalinen regressio (ExpReg)

Sovittaa yhtälön y=abx annettuihin arvoihin käyttäen pienimmän neliösumman menetelmää muunnettuihin arvoihin x ja ln(y). Se näyttää a:n, b:n, r2:n ja r:n arvot.

Logaritminen regressio (LogReg)

Sovittaa yhtälön y=a+b ln(x) annettuihin arvoihin käyttäen pienimmän neliösumman menetelmää muunnettuihin arvoihin ln(x) ja y. Se näyttää a:n, b:n, r2:n ja r:n arvot.

Siniregressio (SinReg)

Sovittaa dataan malliyhtälöä y=a sin(bx+c)+d käyttäen iteratiivista pienimmän neliösumman menetelmää. Se näyttää a:n, b:n, c:n ja d:n arvot. Vähintään neljä datapistettä vaaditaan. Jaksoa kohden tarvitaan vähintään kaksi datapistettä, jotta vältetään virheelliset frekvenssiarviot.

Huomaa: SinReg:n tulos on aina radiaaneja riippumatta Radiaani/Aste-tilan asetuksesta.

Logistinen regressio (d=0) (Logistic)

Sovittaa dataan malliyhtälöä y=c/(1+a*e⁻bx) käyttäen iteratiivista pienimmän neliösumman menetelmää. Se näyttää a:n, b:n ja c:n arvot.

Logistinen regressio (dƒ0) (LogisticD)

Sovittaa dataan malliyhtälöä y=c/(1+a*e(⁻bx))+d käyttäen iteratiivista pienimmän neliösumman menetelmää. Se näyttää a:n, b:n, c:n ja d:n arvot.

Moninkertainen lineaarinen regressio (MultReg)

Laskee listan Y moninkertaisen lineaarisen regression listojen X1, X2, …, X10 suhteen.