
indtastningslinje i funktionstilstand
Indtastningslinjen Grafer og Geometri vises nederst i arbejdsområdet. Du kan bruge den til at angive flere forskrifter for hver af de forskellige graftyper. Standardgraftypen er Funktion, så formlen f1(x)= vises ved start.
Bemærk: Indtastningslinjen skjules automatisk, hvis du ikke indtaster eller redigerer forskrifter. For at vise eller skjule den til hver en tid skal du trykke på / G.
| 1. | Markér den type graf, du vil tegne. |
| - | For at tegne en funktion skal du klikke på Funktion i menuen Grafindtastning /Redigér. |
|
|
Arbejdsområdet og indtastningslinjen ændres til funktionstilstand. Skriv en forskrift for funktionen efter lighedstegnet.
|
|
Skriv koefficienterne i ligningsskabelonen.
| - | Du tegner en parameterfremstilling ved at vælge Parameterfremstilling i menuen Grafindtastning/Redigér. |
|
|
Skriv udtrykkene for xn(t) og yn(t). Du kan frit ændre værdierne for t-min, t-max, og t-trin.
| - | Du kan tegne en polær kurve ved at klikke på Polær i menuen Grafindtastning/Redigér. |
|
|
Skriv et udtryk for rn(q). Du kan frit ændre værdierne for q-minimum og q-maksimum og q-trin.
| - | Du tegner et punktplot ved at klikke på Punktplot i menuen Grafindtastning/Redigér. |
|
|
Arbejdsområdet og indtastningslinjen ændres til punktplottilstand. Klik på var for at vælge en variabel at plotte som x og y for sn. Du kan også skrive navnet på en variabel, der allerede eksisterer, eller definere en liste (skrevet som kommaseparerede elementer omsluttet af krøllede parenteser), for eksempel: {1,2,3}.
| - | Vælg indstillingen til den sekvensgraftype, du vil plotte. |
For at plotte en sekvensgraf som et web-plot eller et tidsplot skal du klikke på Sekvensi menuen Grafindtastning/Redigér og derefter klikke på Sekvens.
|
|
For at plotte et faseplot for en række af sekvenser skal du klikke på Sekvens i menuen Grafindtastning/Redigér og klikke på Brugerdefineret.
|
|
Arbejdsområdet og indtastningslinjen ændrer sig for at vise de nødvendige parametre for den markerede sekvenstilstand. Angiv de nødvendige parametre til plottypen. Med værktøjet Attributter kan du skifte mellem en sekvensgraf som tidsplot og som web-plot.
| 2. | Tryk på · for at tegne forskriften. |
Når du trykker på · for at tegne grafen, skjuler Grafer og Geometri indtastningslinjen og viser grafen uden andre elementer.
Når du har tegnet grafen f1(x) og viser indtastningslinjen igen, viser indtastningslinjen f2(x)=, så du kan indtaste en anden funktion. Hvis du markerer eller sporer en funktion, vises denne funktion i indtastningslinjen.
Når du tegner grafer for flere forskrifte på grafakserne, mærker Grafer og Geometri hver graf med et navn, medmindre Grafer og geometri-indstillingen "Skjul automatisk plotetiketter" er afkrydset. Du kan definere og tegne op til 99 funktioner af hver type. Du kan for eksempel bruge funktionstilstanden til at angive funktionerne (f1(x) - f99(x)). Du kan omdøbe funktioner med brugerdefinerede navne, for eksempel g1(x).
Med historikken for forskrifter kan du vise, redigere og slette forskrifter og grafer.
Historikken lagrer automatisk forskrifter, såsom funktioner fra f1 til f99 og sekvenser fra u1 til u99, for hver opgave. Forskrifterne kan defineres:
| • | I indtastningslinjen for Grafer og Geometri. |
| • | På et andet sted i opgaven, såsom en Beregningsside eller en Noterside. |
| • | I udtryk, der er tegnet med værktøjet Tekst. |
| 1. | Vis indtastningslinjen (/ G), og klik på knappen vis historik  til højre for linjen. til højre for linjen. |
Historikken opfører forskrifterne på en liste i indtastningsrækkefølgen (top til bund).

Bemærk: Historikken viser også hver grafs linjefarve samt knapper til at vise/skjule grafen og ændre visningsattributterne
og ændre visningsattributterne  .
.
| 2. | Brug 9 og : til at flytte op og ned i listen. |
| 3. | Tryk på d for at skjule historikken. |
Med værktøjerne i menuen Undersøg graf kan du finde et punkt af interesse i et angivet område af en funktionsgraf. Vælg et værktøj til at finde nulpunkter, minimum eller maksimum, skæringspunkter eller vendepunktet, differentialkvotienter (dy/dx) eller integraler. For grafer definerede som keglesnit kan du også finde brændpunkter, ledelinje og andre punkter af interesse.
Bemærk (CAS): Du kan også finde vendepunktet.
| 1. | Klik på punktet af interesse i menuen Undersøg graf. Vælg for eksempel Minimum for at finde minimumspunktet. |
Ikonet for det markerede værktøj vises øverst til venstre i arbejdsområdet. Peg på ikonet for at se et værktøjstip om brugen af det markerede værktøj.
| 2. | Klik på den graf, der skal gennemsøges for punkter af interesse. |
Når du udpeger grafen, bliver en punkteret linje vist til markering af den del af grafen, der skal afsøges for punktet af interesse.
Noter:
| - | Hvis du vil finde differentialkvotienten, skal du klikke på grafen i punktet, hvor du vil bestemme differentialkvotienten. |
| - | Du kan vælge værktøjer i kontekstmenuen til at søge punkter af interesse. Hvis du markerer værktøjet Integral eller Differentialkvotient i kontekstmenuen med en funktionsgraf markeret, anvendes den pågældende funktion til at søge efter punktet af interesse. |
| 3. | Tryk på 3 eller 4 for at flytte den punkterede linje til den nedre grænse for søgeintervallet. |
Bemærk: Du kan også skrive et tal, der skal bruges som den nedre grænse for søgeintervallet og trykke på ·.
| 4. | Tryk på · for at markere det punkt, hvor søgningen skal starte. |
Værktøjet skraverer området.
| 5. | Gentag trin 3 og 4 for at indstille den øvre grænse af søgeintervallet. |
Hvis det angivne søgeinterval indeholder punktet af interesse, vises en etikette for punktet. Hvis du ændrer en graf med afmærkede punkter af interesse, skal du huske også at se efter ændringer af disse punkter. Hvis du for eksempel redigerer funktionen i indtastningslinjen eller manipulerer et plot, kan punktet, hvor grafen skærer x-aksen, ændre sig.
Du kan afslutte værktøjet ved at trykke på d eller vælge et andet værktøj. De afmærkede punkter af interesse er fortsat synlige på grafen.
Med indtastningslinjen eller applikationerne Beregninger og Noter kan du angive en funktion med begrænsninger i definitionsmængden. Til sammensatte begrænsninger i definitionsmængden for en funktion anvendes skabelonen for den stykvise funktion ( piecewise() ).
I følgende eksempel er der angivet en funktion med et domæne, der er mindre end 2 og større end -2 i indtastningslinjen:
| 1. | Tryk på / G for at vise indtastningslinjen. |
| 2. | Skriv piecewise(3, x > -2 og x < 2) i indtastningslinjen. |
| 3. | Tryk på · for at tegne funktionen. |
Grafer og Geometri omformaterer forskriften i indtastningslinjen og tegner grafen:
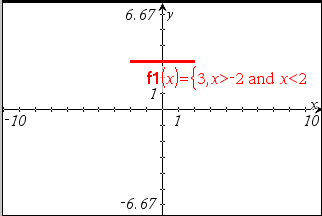
En familie af funktioner adskiller sig ved en eller flere parametre og kan angives ved én enkelt forskrift, der indeholder parameterlister. Sådan tegnes en familie af funktioner:
| 1. | Skriv et udtryk for en familie af funktioner i indtastningslinjen. Sådan angiver du en familie af funktioner. |
| - | Angiv parametrene som et udtryk for flere funktioner ved at bruge formatet f1(x) = {-1,0,1,2} * x + {2,4,6,8} —eller— f1(x) = m*x | m = {1,2,3} |
| - | Skriv som sædvanligt tallisterne eller listerne med variable med krøllede parenteser. Angiv parametre til at tegne en familie på op til 16 funktioner. |
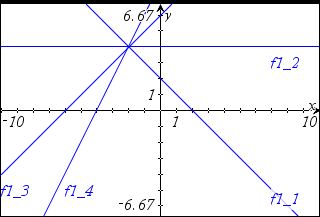
For eksempel angives fire funktioner med udtrykket:
f1(x) = {-1,0,1,2} * x + {2,4,6,8}.
Første funktion, der skal beregnes, er y = -1 * x + 2 og den anden er 0 * x + 4.
| 2. | Tryk på · for at tegne den angivne familie af funktioner. |
Grafer og Geometri opretter og viser en separat graf for hvert medlem af familien af funktioner.
Hver funktion er navngivet (f1_1, f1_2) for at vise dens nummer i rækkefølgen af grafer. Du kan markere, analyse eller spore graferne for at undersøge dem.
Bemærk: Det er ikke muligt at redigere en almindelig funktionsgraf for at ændre den til en familie af funktioner.
I graftegningstilstanden Sekvensgrafer kan du plotte et tidsplot eller web-plot fra indtastningslinjen.
| • | Et tidsplot plotter n på den vandrette akse mod værdien af sekvensen i hvert led, u1(n), på den lodrette akse. Et tidsplot er nyttigt til identifikation af mønstre i talfølger. |
| 1. | Angiv de nødvendige parametre til den sekvenstype, du vil plotte: |
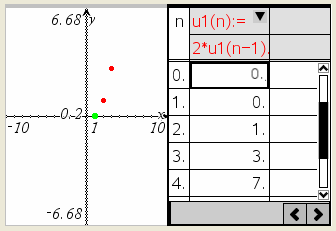
| - | Udtryksfeltet u1(n)= er stedet, hvor du indtaster eller redigerer sekvensen. Skriv det udtryk, der definerer sekvensen. Ledindekset n er en på hinanden følgende række af heltal, der begynder med et nul eller et positivt helt tal. Sekvensnavnet kan indeholde bogstaver, tal og parenteser i formaterne: u1, u1(n), u1(), myseq, myseq(n) eller myseq(). Hvis du skriver sekvensnavnet i formatet u1() eller myseq(), tilføjer applikationen automatisk n. |
| - | Det udtryk, du skriver for en sekvens, kan indeholde en variabel, der er tilknyttet en skyder. |
| - | Parameteren Startled er det første led, der skal beregnes for en rekursiv sekvens. Hvis sekvensudtrykket kalder mere end ét forudgående led, såsom u1(n-1) og u1(n-2), skal du skrive flere begyndelsesled. Adskil flere begyndelsesled med kommaer. |
| - | Trin-intervallet n er det mindste indeks, maksimale indeks og det trinvise spring, der anvendes til graftegningen. |
I u1(n) feltet kan du for eksempel skrive udtrykket 2*u1(n‑1) + 1. Der kræves ikke indtastning af første led eller trinstørrelse i dette tilfælde.
| 2. | Efter indtastning af parametrene trykker du på · for at tegne den angivne sekvens. |
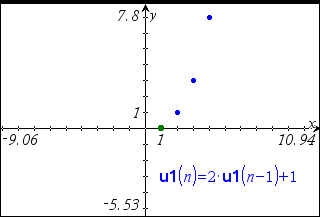
Sekvensgrafen indeholder et punkt for hvert led i sekvensen.
Bemærk: Hvis du plotter en sekvens, og hvis den variabel, der anvendes til at angive den, senere ændres til en anden type (såsom til en funktion), slettes den plottede sekvens automatisk.
| 3. | Klik på sekvensgrafen, og udforsk den tegnede sekvensgraf med værktøjerne i Grafer og Geometri. |
| - | Klik på sekvensgrafen for at se dens ligning og navnet for grafen. |
| - | Du kan animere en skyder, der er tildelt til at bruge en variabel i ligningen for en sekvensgraf for at observere ændringerne i plottet. |
| - | Højreklik på arbejdsområdet, og klik på Grafsporing i kontekstmenuen for at løbe gennem grafpunkterne og fremhæve værdierne i sekvensen. |
Håndholdt: Tryk på / b, og markér Grafsporing for at løbe igennem grafpunkterne og fremhæve værdierne i sekvensgrafen.
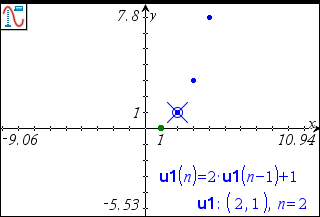
| - | Tryk på / T for at vise en tabel med de værdier, der blev fundet under beregning af sekvenserne med på hinanden følgende heltalsværdier. |
| - | Grib og træk i det punkt, der repræsenterer det første led. Mens du trækker i punktet hørende til startleddet, ændres dets værdi. Sekvensgrafdefinitionen i indtastningslinjen opdateres automatisk med de ændringer, du foretager, ved at manipulere punktet for startleddet. |
Med et brugerdefineret plot kan du vise en sammenhæng mellem to sekvenser ved at plotte den ene sekvens på x -aksen og den anden på y -aksen.
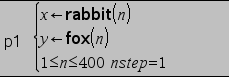
Når du definerer et brugerdefineret plot angiver du variabelnavnene på to definerede sekvenser (i applikationen Grafer og Geometri) og tildeler hver sekvens en akse. I dette afsnit demonstreres, hvordan du kan bruge en brugerdefineret sekvens og rovdyr-byttedyr-modellen fra biologi til at bestemme det antal kaniner og ræve, der opretholder ligevægten i populationerne.
kanin(n) = kanin(n-1) * (1 +,05-,001 * ræv(n-1))
ræv(n) = ræv(n-1) * (1 +,0002* kanin(n-1) -,03), hvor:
,05 = vækstraten for kaniner, hvis der ikke findes ræve,
,001 = hastigheden, hvormed ræve kan dræbe kaniner,
,0002 = vækstraten for ræve, hvis der findes kaniner,
,03 = dødsraten for ræve, hvis der ikke findes kaniner.
| 1. | I menuen Grafindtastning/Redigér skal du klikke på Sekvens og klikke på Sekvens. Med modelligningen kan du definere kanin og rævesekvenser over en cyklus på 400 generationer. Vi går ud fra, at der til at begynde med er 200 kaniner og 50 ræve. |

Bemærk: For at få et mindre overlæsset billede, kan du vælge Skjul/Vis i menuen Handlinger for at skjule sekvensernekanin(n) og ræv(n) i arbejdsområdet.
| 2. | I menuen Graftype skal du klikke på Sekvens og klikke på Brugerdefineret. |
| 3. | Skriv kanin(n) som x-aksesekvens, tryk derefter på e, og skriv ræv(n) som y-aksesekvens. |
Bemærk: Du kan også klikke på  (eller trykke på h) for at vælge navnet på en tidligere defineret sekvens eller angive navnet på en ny sekvens, som du kan definere senere.
(eller trykke på h) for at vælge navnet på en tidligere defineret sekvens eller angive navnet på en ny sekvens, som du kan definere senere.
| 4. | Tryk på e for at gå til næste linje, og indstil n-trinnet og intervallet for n. Til dette eksempel er n indstillet til mellem 1 og 400, og n-trin er på standardværdien 1. |
| 5. | Tryk på · for at oprette den brugerdefinerede sekvens. |
Bemærk: Klik på Zoom – Tilpasning i menuen Vindue/Zoom for at justere vinduesindstillingerne.
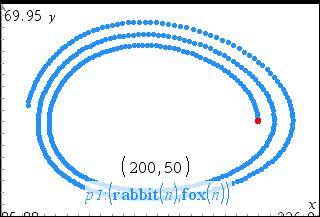
| 6. | Undersøg det brugerdefinerede plot ved at gribe og trække i det punkt, der repræsenterer det første led. |
Når du trækker i startpunktet, ændres dets værdi, og de første led for kanin og ræv opdateres automatisk.


I dette eksempel demonstrerer en manipulation af startpunktet hørende til det første led, at ligevægtspunktet i kanin- og rævepopulationerne over en cyklus på 400 generationer = (150, 50).
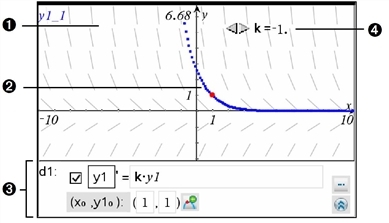
Du kan studere lineære og ikke-lineære differentialligninger og systemer af almindelige differentialligninger (ODE'er), inklusive logistiske modeller og Lotka-Volterra-ligninger (rovdyr-byttedyr-model). Du kan også plotte linjeelementer og retningsfelter med interaktiv anvendelse af Euler- og Runge-Kutta-metoder.
|
À |
Linjeelementer |
|||||||||||||||
|
Á |
En løsningskurve går gennem punktet hørende til startbetingelsen |
|||||||||||||||
|
 |
ODE-editor:
|
|||||||||||||||
|
à |
Skyder til at styre koefficienten k i den sædvanlige differentialligning af første orden |
| 1. | I menuen Grafindtastning /Redigér skal du klikke på Differentialligning. |
Indtastningslinjen viser et ODE-redigeringsfelt til definition af den næste tilgængelige ODE. ODE'en tildeles automatisk en afhængig variabel, såsom "y1".

Bemærk: Du kan indtaste et andet navn for den afhængige variabel til erstatning og derefter bruge dette navn i differentialligningen på den højre side af “=”-symbolet.
| 2. | Navigér til feltet for ligningen, og indtast udtrykket, der definerer differentialligningen. Du kan for eksempel indtaste -y1+0.1*y1*y2. |

| 3. | Indtast begyndelsesbetingelsen for den uafhængige værdi for x0 og for y10. |
Noter:
| - | Værdien(erne) x0 er fælles for alle ODE'erne i en opgave, men kan kun indtastes eller redigeres i den første ODE. De vises som ikke-redigerbare i de andre ODE'er. |
| - | Du kan slette en eksisterende begyndelsesbetingelse ved at rydde betingelsens x0- og y0-felter. |
| 4. | Hvis du ønsker at undersøge flere begyndelsesbetingelser for den aktuelle ODE, skal du klikke på knappen Tilføj startbetingelse  og indtaste betingelserne. og indtaste betingelserne. |
| 5. | Klik på knappen Redigér parametre  for at vise eller indstille plotparametre. for at vise eller indstille plotparametre. |
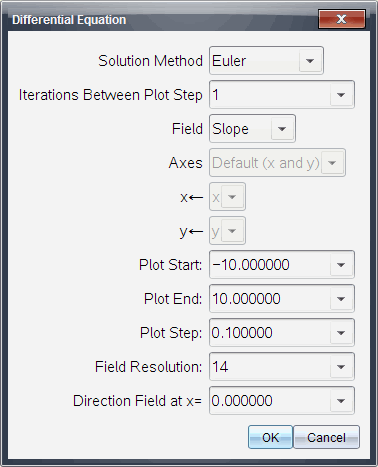
| 6. | Der henvises til oversigten over indstillinger, der følger denne procedure. Markér en numerisk løsningsmetode og yderligere plotparametre. Du kan ændre disse parametre efter behov. |
| 7. | Klik på OK. |
| 8. | Indtast yderligere ODE'er ved at trykke på pil ned for at få vist det næste ODE-redigeringsfelt. |
Når du trykker på · eller på pil op eller pil ned for at navigere mellem de ODE'er, du allerede har defineret, opdateres grafen for at vise ændringerne. Én løsning til ODE'en er tegnet for hver startbetingelse der er knyttet til den aktive ODE (valgt med et afkrydsningsfelt).
|
Løsningsmetode |
Markér Euler eller Runge-Kutta som numerisk løsningsmetode. |
|||||||||
|
Iterationer mellem plottrin |
Beregningsnøjagtighed (kun for Euler-løsningsmetoden). Skal være en heltalsværdi >0. Markér pil ned, og herefter Standard for at gendanne standardværdierne. |
|||||||||
|
Fejltolerance |
Beregningsnøjagtighed kun for Runge-Kutta-løsningsmetoden. Skal være en flydende decimaltalværdi |1×10-14. Markér pil ned, og herefter Standard for at gendanne standardværdierne. |
|||||||||
|
Retningsfelt |
Intet – intet retningsfelt. Denne mulighed gælder for alle ODE'er, men den er den eneste mulighed, når tre eller flere førsteordens ODE'er er aktive. Tegner en kombination af løsninger og/eller værdier for en eller flere ODE'er (i overensstemmelse med brugerkonfigurerede Akseindstillinger). Hældning – plotter et felt af linjelementer, der repræsenterer familien af løsninger på en enkelt førsteordens ODE. Der skal være præcist én ODE aktiv. Indstiller Akser til Standard (x og y). Indstiller den vandrette akse til x (den uafhængige værdi). Indstiller den lodrette akse til y (løsningen til ODE'en). Retning – tegner et retningsfelt i faseplanet, der repræsenterer retningsvektoren for et system af to førsteordens‑ ODE'er (som angivet af den Brugerdefinerede Akseindstilling). Der skal være præcist to ODE'er aktive. |
|||||||||
|
Akser |
Standard (x og y) – plotter x på x-aksen og y (løsningerne til de aktive differentialligninger) på y-aksen. Brugerdefineret – lader dig markere de værdier, der skal plottes på henholdsvis x- og y-aksen. Gyldige indtastninger inkluderer:
|
|||||||||
|
Plotstart |
Indstiller den uafhængige variabelværdi, hvor løsningskurven starter. |
|||||||||
|
Plotslut |
Indstiller den uafhængige variabelværdi, hvor løsningsplottet stopper. |
|||||||||
|
Plottrin |
Indstiller det trinvise spring for den uafhængige variabel, der benyttes i plottet. |
|||||||||
|
Feltopløsning |
Indstiller antallet af rækker og søjler i retningsfeltet, der bruges til at tegne linjeelementer eller retningsvektorer. Du kan kun ændre denne parameter, hvis Felt = Retning eller Hældning. |
|||||||||
|
Retningsfelt i x= |
Indstiller den uafhængige variabelværdi, hvor retningsfeltet tegnes, når ikke-autonome ligninger plottes (dem, der referer eksplicit til tidsparameteren x). Ignoreres, når der plottes autonome ligninger. Du kan kun ændre denne parameter, hvis Felt = Retning. |
Visningen Graftegning giver dig mulighed for at tegne og udforske lineære ligninger og andengradsligninger for keglesnit i et todimensionalt koordinatsystem. Du kan oprette og analysere linjer, cirkler, ellipser, parabler, hyperbler og generelle keglesnit.
Indtastningslinjen gør det enkelt at indtaste ligningen ved at vise en skabelon for typen af den ligning, som du vælger.
| 1. | I menuen Grafindtastning/Redigér skal du klikke på Ligning > Ellipse og klikke på ligningen. |
Indtastningslinjen viser skabelonen.
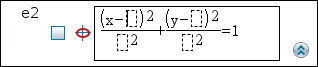
| 2. | Skriv startværdier for koefficienterne i de beregnede felter. Brug piletasterne til at navigere mellem koefficienterne. |
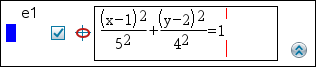
| 3. | Tryk på · for at tegne ligningen. |
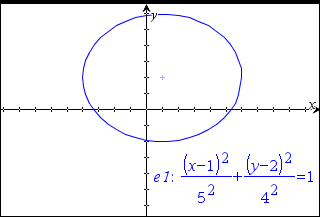
| 4. | Træk i ellipsen ved at gribe fat i dens centrum for at udforske effekten af parallelforskydningen i ligningen. |
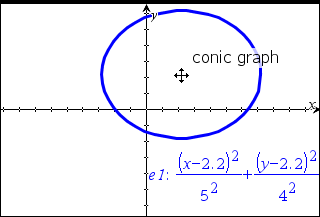
| 5. | Brug analyseværktøjerne, såsom Undersøg graf > Undersøg keglesnit > Brændpunkter til at udforske grafen yderligere. |
Bemærk: Keglesnittets type bestemmer, hvilke analyseværktøjer du kan bruge. I tilfælde af ellipsen kan du få adgang til dens centrum, toppunkter, brændpunkter, symmetriakser, ledelinjer, excentricitet og bredde parameter (latus rectum).
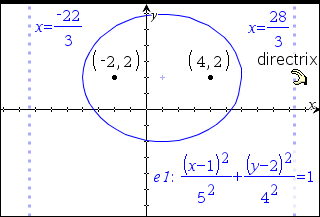
| 6. | For at udforske både parallelforskydning og multiplikation skal du definere en ellipse, der bruger variable for h, k, a og b-koefficienterne. Opret skydere til at variere parametrene. |
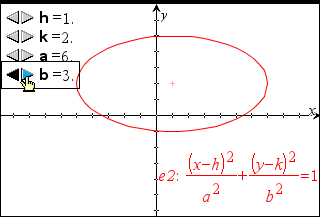
Du kan tegne en "x=" eller "y="-ligning ved at indtaste den i et tekstfelt og trække teksten til en akse.
Når du slipper teksten, tegner Grafer og ligningen og tilføjer den til den øverste del af funktionshistorikken. Du kan redigere ligningen (du kan for eksempel ændre den til en ulighed), men du kan ikke skifte mellem x= and y=.
| 1. | Åbn menuen Handlinger, og klik på Tekst. |
| 2. | Klik i arbejdsområdet for at placere tekstfeltet, og skriv derefter den ligning, du vil tegne. |
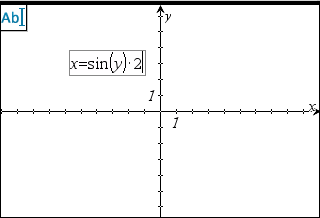
| 3. | Træk teksten, og slip den på en akse. |
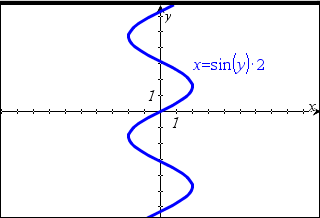
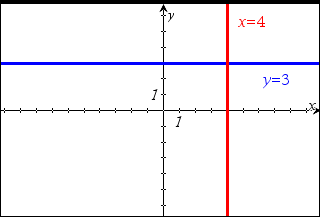
| 1. | Opret et tekstfelt, og skriv en ligning til en lodret linje, såsom x=4, eller en vandret linje, såsom y=3. |
| 2. | Træk teksten til en akse. |
Efter du har plottet en linje, kan du trække for at parallelforskyde eller dreje den eller fastgøre den for at bruge den som en fastlåst referencelinje.
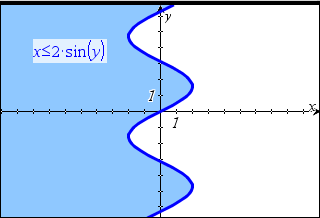
Du kan tegne uligheder, der bruger operatorerne >, <, { eller |. Områder, der opfylder uligheden, bliver vist med skygge. Hvis skraverede områder af to eller flere uligheder overlapper, tones overlapningsområdet mørkere.
| 1. | Opret et tekstfelt, og indtast ulighedsudtrykket, såsom x<2*sin(y). |
Bemærk: For at udtrykke { eller | kan du skrive <= eller >= eller vælge tegnet i Symbolpaletten.
| 2. | Træk teksten til en akse. |
Standardnavnet for funktioner er fn(x). (Indekset repræsenteret ved tallet n øges i takt med, at du angiver flere funktioner). Du kan udskifte standardnavnet med et navn efter eget valg.
| 1. | Placer din markør til højre for lighedstegnet i indtastningslinjen. |
| 2. | Vælg standardnavnet. |

| 3. | Skriv med bogstaver/tal det navn, du vil bruge, og skriv derefter den funktion eller forskrift, du vil tegne. |

| 4. | Tryk på · for at tegne grafen for funktionen. |
Bemærk, at navnet ved siden af grafen er identisk med det, du har indtastet.

Bemærk: For at fortsætte med at anvende brugerdefineret navngivning skal du manuelt omdøbe hver ny funktion, når den indtastes.
| 1. | I menuen Grafindtastning/Redigér skal du klikke på grafens type, såsom Funktion. |
Indtastningslinjen for den markerede graftype vises.
| 2. | Brug tasterne pil op/pil ned til at gå igennem historikken for forskrifterne og vælge grafen. |
| 3. | Tilpas forskriften efter behov. |

| 4. | Tryk på · for at tegne grafen for den reviderede funktion. |
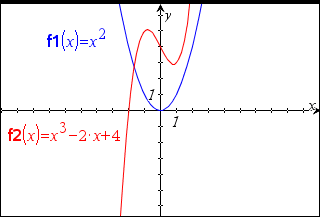
| 1. | I menuen Handlinger skal du klikke på Skjul/Vis. |
Værktøjsikonet Skjul/vis bliver vist øverst i arbejdsområdet.
| 2. | Klik på grafen for de funktioner, du vil skjule. Du kan også klikke på andre objekter, du vil skjule. |
Objekter, du klikker på, mens værktøjet er aktivt, vises nedtonet.
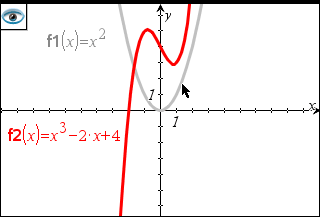
| 3. | Tryk på d for at afslutte værktøjet Skjul/Vis. |
Den skjulte funktion forsvinder. For at vise skjulte elementer igen skal du gentage disse trin.
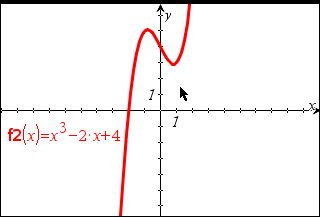
| 1. | Markér funktionen ved at klikke på dens graf. |
| 2. | Slet funktionen ved at trykke på Back Space-tasten eller .. |
Funktionen fjernes fra arbejdsområdet og fra listen med tegnede funktioner.
Visse funktioner kan du parallelforskyde, strække og/eller dreje ved at gribe i grafen og manipulere den.
| ¢ | Gå til menuen Handlinger, klik på Markør, og gå til den graf, du vil manipulere. |
Markøren ændres for at vise en understøttet manipulation (for eksempel til õ, ö, eller é), hvis du holder markøren over en tegnet funktion, du kan gribe i og manipulere.
Når du ændrer grafen, opdateres ligningen for grafen for at afspejle ændringerne. Du kan manipulere følgende funktionstyper:
| • | Konstant funktion; y=b, x=b |
| • | Lineær funktion; y=ax+b, x=ay+b |
| • | Kvadratisk funktion; y=a(x-b)2+c, x=a(y-b)2+c |
| • | Kvadratisk funktion; y=ax2+bx+c, x=ay2+by+c |
| • | Eksponentiel funktion; y=exp(ax+b)+c, x=exp(ay+b)+c |
| • | Eksponentiel funktion; y=b*exp(ax)+c, x=b*exp(ay)+c |
| • | Eksponentiel funktion; y=d*exp(ax+b)+c, x=d*exp(ay+b)+c |
| • | Logaritmisk funktion; y=a*ln(cx+b)+d, x=a*ln(cy+b)+d |
| • | Sinussvingning; y=a*sin(cx+b)+d, x=a*sin(cy+b)+d |
| • | Cosinussvigning; y=a*cos(cx+b)+d, x=a*cos(cy+b)+d |
| ¢ | Grafen kan parallelforskydes ved at gribe tæt på grafens midte og derefter trække. |
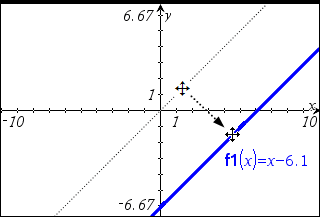
| ¢ | Grafen kan drejes ved at gribe tæt på grafens ender, og derefter trække. |
| ¢ | Grafen kan parallelforskydes ved at gribe tæt på grafens toppunkt og derefter trække. |
| ¢ | Grafen kan strækkes ved at gribe uden for grafens toppunkt og derefter trække. |
| ¢ | Grafen kan parallelforskydes ved at gribe tæt på den lodrette symmetriakse og derefter trække |
| ¢ | Grafen kan strækkes ved at gribe uden for grafens lodrette symmetriakse og derefter trække. |
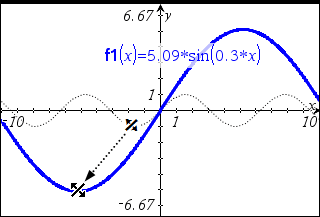
Denne metode benytter menuen Undersøg graf. Alternativt kan du oprette en tangent på grafen som hjælp til at visualisere hældningen og derefter anvende menuen Måling til at måle den.
| 1. | I menuen Undersøg graf skal du klikke på dy/dx. |
| 2. | Klik på det punkt på grafen, hvor du vil bestemme differentialkvotienten. |
Værdien af differentialkvotienten for det markerede punkt bliver vist på grafen.
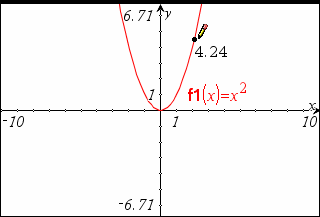
Bemærk: Du kan bestemme differentialkvotienten af en specifik værdi af x eller y med kontekstmenuen for punktet for at vise dets koordinater og derefter redigere x -eller y-koordinaten.
Du kan vise en tabel med funktionsværdier for funktioner i den aktuelle opgave.
Under visning af tabellen kan du ændre indstillingerne for tabellen, slette kolonner, tilføje værdier for flere funktioner og redigere det udtryk, der definerer en funktion. For yderligere oplysninger henvises der til Brug af Lister og Regneark.
| ¢ | I menuen Tabel skal du klikke på Delt-skærmbillede -tabel. |
Tabellen bliver vist med kolonner med værdier for de aktuelt definerede funktioner.
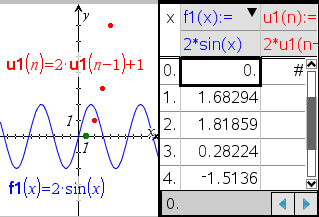
Øverst i hver kolonne kan du vælge den funktion, der skal vises i kolonnen.
| ¢ | I menuen Tabel skal du klikke på Fjern tabel. |