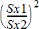Ondersteunde statistische toetsen
Hypothesetoetsen zijn beschikbaar in de toepassing Lijsten & Spreadsheets. Zie voor meer informatie over deze functies de TI-Nspire™-handleiding.
In bepaalde wizards voor statistische toetsen is er een selectievakje voor Tekenen. Dit vakje is standaard niet geselecteerd. Door dit vakje aan te kruisen wordt er een Gegevensverwerking & Statistiek-werkgebied op de pagina gecreëerd, en worden de resultaten in dat werkgebied geplot.
z -toets (zTest)
Voert een hypothesetoets uit voor één onbekend populatiegemiddelde, m, wanneer de populatiestandaarddeviate, s, bekend is. De nulhypothese H0: m=m0 wordt getoetst tegen één van de onderstaande alternatieven.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Deze toets wordt gebruikt voor grote populaties die normaal verdeeld zijn. De standaarddeviatie moet bekend zijn.
Deze toets kan gebruikt worden om te bepalen of het verschil tussen een steekproefgemiddelde en een populatiegemiddelde statistisch significant is wanneer u de ware standaarddeviatie voor een populatie weet.
t -toets (tTest)
Voert een hypothesetoets uit voor één onbekend populatiegemiddelde, m, wanneer de populatiestandaarddeviate, s, onbekend is. De nulhypothese H0: m=m0 wordt getoetst tegen één van de onderstaande alternatieven.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Deze toets is gelijk aan een z-toets, maar wordt gebruikt wanneer de populatie klein en normaal verdeeld is. Deze toets wordt vaker gebruikt dan de z-toets, omdat kleine steekproefpopulaties vaker voorkomen in de statistiek dan grote populaties.
Deze toets wordt gebruikt om te bepalen of twee normaal verdeelde populaties gelijke gemiddelden hebben, of om te bepalen of een steekproefgemiddelde significant verschilt van een populatiegemiddelde en de populatiestandaarddeviatie onbekend is.
z-toets met gepaarde steekproeven (zTest_2Samp)
Toetst de gelijkheid van de gemiddelden van twee populaties (m1 en m2) op basis van onafhankelijke steekproeven wanneer beide populatiestandaarddeviaties (s1 en s2) bekend zijn. De nulhypothese H 0:m1=m2 wordt getoetst tegen één van de onderstaande alternatieven.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
t-toets met gepaarde steekproeven (tTest_2Samp)
Toetst de gelijkheid van de gemiddelden van twee populaties (m1 en m2) op basis van onafhankelijke steekproeven wanneer geen van beide populatiestandaarddeviaties (s1 of s2) bekend is. De nulhypothese H0: m1=m2 wordt getoetst tegen één van de onderstaande alternatieven.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
z-toets met 1 prop (zTest_1Prop)
Berekent een toets voor een onbekende proportie van successen (prop). Als invoer wordt het aantal successen x in de steekproef en het aantal observaties n in de steekproef genomen. Een -z-toets met 1 proportie test de nulhypothese H0: prop=p0 tegen een van de onderstaande alternatieven.
| • | Ha: propƒp0 |
| • | Ha: prop<p0 |
| • | Ha: prop>p0 |
Deze toets wordt gebruikt om te bepalen of de kans op succes die aangetroffen wordt in een steekproef significant verschilt van de kans op succes in de populatie, of dat dit het gevolg is van een steekproeffout, afwijking of andere factoren.
z-toets met 2 prop (zTest_2Prop)
Berekent een toets om de proportie van successen (p1 en p2) van twee populaties te vergelijken Als invoer wordt het aantal successen in elke steekproef (x1 en x2) en het aantal observaties in elke steekproef genomen (n1 en n2). - z-toets met 2 proporties toetst de nulhypothese H0: p1=p2 (met behulp van de samengestelde steekproefproportie Ç) tegen één van de onderstaande alternatieven.
| • | Ha: p1ƒp2 |
| • | Ha: p1<p2 |
| • | Ha: p1>p2 |
Deze toets wordt gebruikt om te bepalen of de kans op succes die aangetroffen wordt in twee steekproeven gelijk is.
c2GOF (c2GOF)
Voert een toets uit om te bevestigen dat de steekproefgegevens afkomstig zijn uit een populatie met de gespecificeerde verdeling. c2 GOF kan bijvoorbeeld bevestigen dat de steekproefgegevens afkomstig waren uit een normale verdeling.
c2 2-voudige toets (c22-voudige)
Berekent een chi-kwadraat-toets voor afhankelijkheid in de kruistabel met aantallen uit de gespecificeerde geobserveerde matrix. De nulhypothese H0 voor een kruistabel is: er bestaat geen afhankelijkheid tussen rijvariabelen en kolomvariabelen. De alternatieve hypothese is: de variabelen zijn afhankelijk.
F-toets met 2 steekproeven (FTest_2Samp)
Berekent een F--toets om twee normale populatie-standaarddeviaties (s1 en s2) te vergelijken. De gemiddelden en standaarddeviaties van de populatie zijn allemaal onbekend. De F-toetsmet 2 steekproeven, die de verhouding van steekproefvarianties Sx12/Sx22 gebruikt, toetst de nulhypothese H0: s1=s2 tegen een van de onderstaande alternatieven.
| • | Ha: s1ƒs2 |
| • | Ha: s1<s2 |
| • | Ha: s1>s2 |
Hieronder volgt de definitie voor de F-toets met 2steekproeven.
|
Sx1, Sx2 |
= |
Steekproefstandaarddeviaties met respectievelijk n1N1 en n2N1 vrijheidsgraden df. |
|
|
|
F-grootheid = |
|
df(x, n1N1, n2N1) |
= |
Fpdf( ) met vrijheidsgraden df, n1N1 en2N1 |
|
p |
= |
gerapporteerde p-waarde |
F--toets met 2 steekproeven voor de alternatieve hypothese s1 > s2.
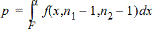
F--toets met steekproeven voor de alternatieve hypothese s1 < s2.
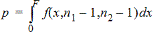
F--toets met 2 steekproeven voor de alternatieve hypothese s1ƒs2. De grenzen moeten aan het volgende voldoen:
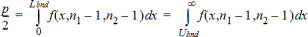
waarbij [Ondergrens,Bovengrens]=onder- en bovengrenzen ([Lbnd,Ubnd])
De F--statistiek wordt gebruikt als de grens die de kleinste integraal produceert. De andere grens wordt geselecteerd zodat de bovenstaande integraalvergelijking juist is.
t-toets lineaire regressie (LinRegtTest)
berekent een lineaire regressie op de gegevens en een t-toets op de waarde van de helling b en de correlatiecoëfficiënt r voor de vergelijking y=a+bx. De nulhypothese H0: b=0 (equivalent aan r=0) wordt getoetst tegen één van de onderstaande alternatieven.
| • | Ha: bƒ0 en rƒ0 |
| • | Ha: b<0 en r<0 |
| • | Ha: b>0 en r>0 |
Meervoudige reg.-toets (MultRegTest)
Berekent een lineaire regressie op de gegevens, en geeft de F-toetsingsgrootheid voor lineariteit.
Zie voor meer informatie de TI-Nspire™ handleiding.
ANOVA (ANOVA)
Berekent een enkelvoudige variantieanalyse voor het vergelijken van de gemiddelden van 2 tot 20 populaties. De ANOVA-procedure voor het vergelijken van deze gemiddelden impliceert analyse van de variatie in de steekproefgegevens. De nulhypothese H0: m1=m2=...=mk wordt getest tegen de alternatieve hypothese Ha: niet alle m1...mk zijn gelijk.
De ANOVA-toets is een methode om te bepalen of er een significant verschil is tussen de groepen vergeleken met het verschil dat optreedt binnen elke groep.
Deze toets wordt gebruikt om te bepalen of de variatie van gegevens van steekproef tot steekproef een statistisch significante invloed van een andere factor laat zien dan van de variatie binnen de gegevensverzamelingen zelf. Een dozeninkoper voor een verzendbedrijf wil bijvoorbeeld drie verschillende dozenfabrikanten beoordelen. Hij krijgt voorbeelddozen van alle drie de leveranciers. ANOVA kan hem helpen te bepalen of de verschillen tussen de steekproeven significant zijn vergeleken met de verschillen binnen elke steekproef.
ANOVA 2-voudige (ANOVA2way)
Berekent een tweevoudige variantieanalyse voor het vergelijken van de gemiddelden van twee tot 20 populaties. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten.
De tweewegs ANOVA-analyse van variantie onderzoekt de effecten van twee onafhankelijke variabelen en helpt om te bepalen of deze elkaar beïnvloeden met betrekking tot de afhankelijke variabele. (Met andere woorden, als de twee onafhankelijke variabelen inderdaad van invloed zijn op elkaar, dan kan hun gecombineerde effect groter of kleiner zijn dan de som van de effecten van elke onafhankelijke variabele.)
Deze toets wordt gebruikt om verschillen te beoordelen net als bij de ANOVA-analyse, maar met toevoeging van een andere mogelijke invloed. Om door te gaan op het voorbeeld met de dozen: met tweewegs-ANOVA zou u de invloed van het materiaal van de dozen op de waargenomen verschillen kunnen onderzoeken.
Een alternatieve hypothese selecteren (ƒ< >)
De meeste editors op het gebied van interferentiële statistiek voor de hypothesetoetsen verzoeken u om één van drie alternatieve hypotheses te selecteren.
| • | De eerste is een ƒ alternatieve hypothese, zoals mƒm0 bij de z toets. |
| • | De tweede is een < alternatieve hypothese, zoals m1<m2 bij de t-toets met 2 steekproeven. |
| • | De derde is een > alternatieve hypothese, zoals p1>p2 bij de z-toets met 2 prop. |
Om een alternatieve hypothese te selecteren verplaatst u de cursor naar het betreffende alternatief en drukt u op Enter.
De gepoolde optie selecteren
Gepoold (alleen bij t toets met 2- steekproeven en t interval met 2- steekproeven) specificeert of de varianties gepoold moeten worden voor de berekening.
| • | Selecteer Nee als u niet wilt dat de varianties gepoold worden. Populatievarianties kunnen ongelijk zijn. |
| • | Selecteer Ja als u wilt dat de varianties gepoold worden. Populatievarianties worden verondersteld gelijk te zijn. |
Om de optie Gepoold te kiezen selecteert u Ja uit de lijst.