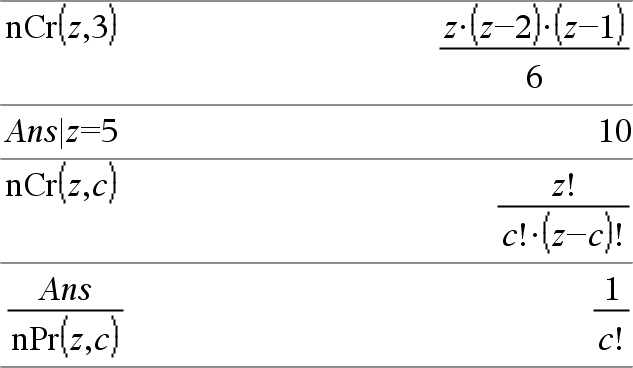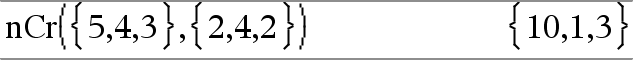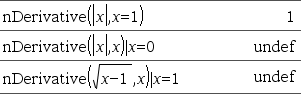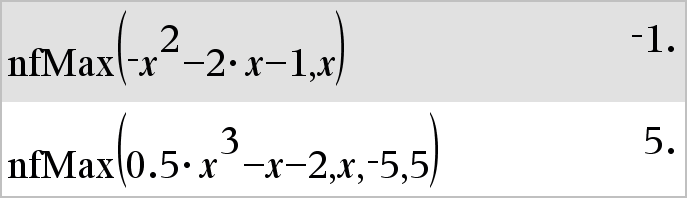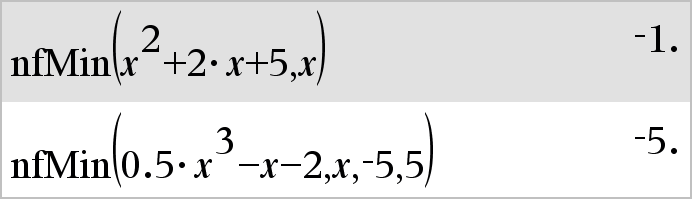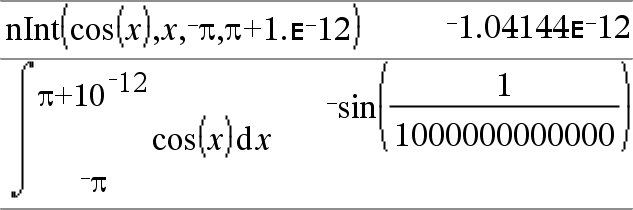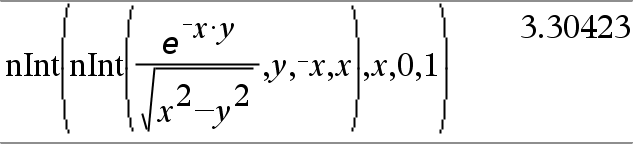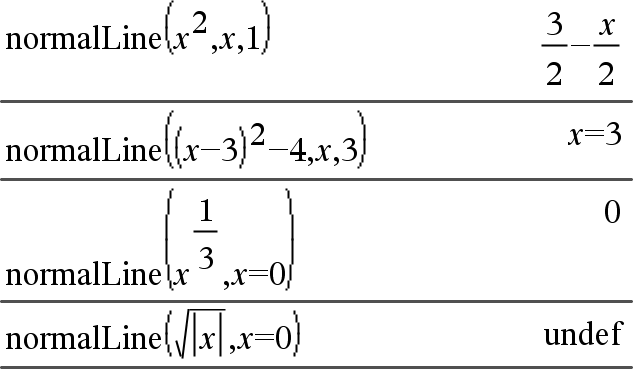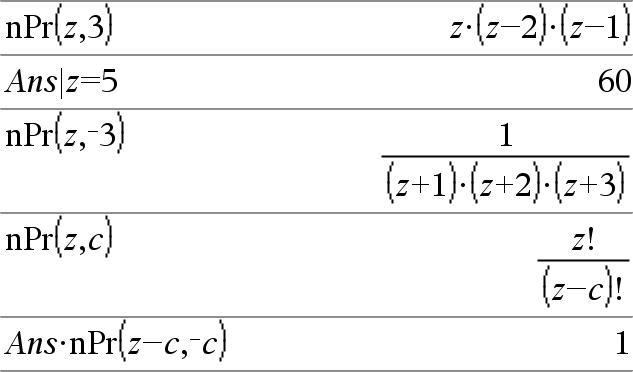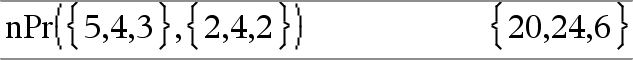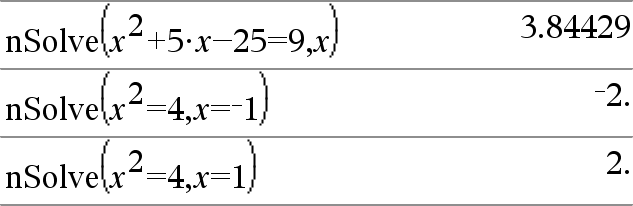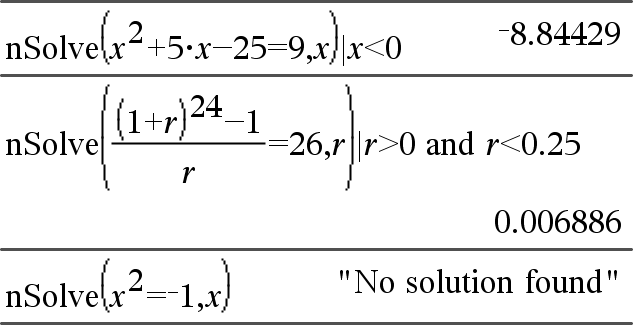|
/= näppäimet |
|
|
BoolenLaus1 Antaa vastauksena loogisen Listojen ja matriisien kohdalla vastauksena on vertailuja elementti elementiltä. |
|
|
Kokonaisluku1 Vertaa kahta reaalikokonaislukua bitti bitiltä Kokonaisluvut voi syöttää minkä tahansa luvun kantalukuna. Binaarisen syötteen edelle tulee merkitä etumerkki 0b ja heksadesimaalisen syötteen edelle 0h. Jos etumerkkiä ei ole, kokonaislukuja käsitellään desimaalilukuina (kantaluku 10). |
|
|
Katalogi > |
|
|
nCr(Laus1, Laus2)Þlauseke Kokonaisluvulle Laus1 ja Laus2 sekä Laus1 | Laus2 | 0, nCr() on Laus1:n asioiden kombinaatioiden lukumäärä, joita otetaan Laus2:n verran kerrallaan. (Tästä käytetään myös nimitystä binomikerroin.) Kumpikin argumentti voi olla kokonaisluku tai symbolinen lauseke. nCr(Laus, 0)Þ1 nCr(Laus, negKokonaisluku)Þ0 nCr(Laus, posKokonaisluku)Þ Laus·(LausN1)... (LausNposKokonaisluku+1)/ posKokonaisluku! nCr(Laus, eiKokonaisluku)Þlauseke!/ ((LausNeiKokonaisluku)!·eiKokonaisluku!) |
|
|
nCr(Lista1, Lista2)Þlista Laskee listan kombinaatioista kahden listan sisältämiin vastaaviin elementtipareihin perustuen. Argumenttien on oltava samankokoisia listoja. |
|
|
nCr(Matriisi1, Matriisi2)Þmatriisi Laskee matriisin kombinaatioista kahden matriisin sisältämiin vastaaviin elementtipareihin perustuen. Argumenttien on oltava samankokoisia matriiseja. |
|
|
Katalogi > |
|
|
Laskee numeerisen derivaatan käyttäen automaattisia derivointimenetelmiä. Kun Arvo määritetään, se ohittaa mahdolliset aikaisemmat muuttujamääritykset tai mahdolliset muuttujan nykyiset “|” -sijoitukset. Derivaatan Asteen on oltava 1 tai 2. |
|
|
Katalogi > |
|
|
newList(numElementit)Þlista Antaa tuloksena listan, jonka koko on numElementit. Jokainen elementti on nolla. |
|
|
Katalogi > |
|
|
newMat(numRivit, numSarakkeet)Þmatriisi Antaa tuloksena nollamatriisin, jonka koko on numRivit ja numSarakkeet. |
|
|
Katalogi > |
|
|
nfMax(Laus, Muutt)Þarvo Laskee muuttujan Muutt numeerisen ehdotusarvon, jossa lausekkeen Laus paikallinen maksimi esiintyy. Jos ilmoitat alarajan ja ylärajan, funktio etsii suljetulta väliltä [alaraja,yläraja] paikallista maksimia.
|
|
|
Katalogi > |
|
|
nfMin(Laus, Muutt)Þarvo Laskee muuttujan Muutt numeerisen ehdotusarvon, jossa lausekkeen Laus paikallinen minimi esiintyy. Jos ilmoitat alarajan ja ylärajan, funktio etsii suljetulta väliltä [alaraja,yläraja] paikallista minimia.
|
|
|
Katalogi > |
|
|
nInt(Laus1, Muutt, Ala, Ylä)Þlauseke Jos integroitava funktio Laus1 ei sisällä muita muuttujia kuin Muutt, ja jos Ala ja Ylä ovat vakioita, positiivinen ˆ tai negatiivinen ˆ, tällöin nInt() laskee likiarvon lausekkeesta ‰(Laus1, Var, Ala, Ylä). Tämä likiarvo on integrandin välillä Ala<Muutt<Ylä olevien joidenkin otosarvojen painotettu keskiarvo. |
|
|
Tavoitteena on kuusi merkitsevää numeroa. Adaptiivinen algoritmi päättyy, kun näyttää todennäköiseltä, että tavoite on saavutettu, tai kun näyttää epätodennäköiseltä, että lisäotokset tuottaisivat merkittävää parannusta. Näkyviin tulee viesti (Questionable accuracy (Kyseenalainen tarkkuus)), kun näyttää siltä, että tavoitetta ei ole saavutettu. |
|
|
Sijoita nInt()-komentoa sisäkkäin, jos haluat suorittaa moninkertaisen numeerisen integroinnin. Integroinnin raja-arvot voivat riippua niiden ulkopuolella olevista integrointimuuttujista. |
|
|
Huomaa: Katso myös ‰(), täältä. |
|
|
Katalogi > |
|
|
nom(efektiivinenKorko,CpY)Þarvo Talouslaskentatoiminto, joka muuntaa efektiivisen vuosikoron efektiivinenKorko nimelliskoroksi, kun CpY määritetään korkojaksojen lukumääräksi vuodessa. efektiivinenKorko on oltava reaaliluku, ja CpY:n on oltava reaaliluku > 0. Huomaa: Katso myös eff(), täältä. |
|
|
/= näppäimet |
|
|
BoolenLaus1
Antaa vastauksena loogisen Listojen ja matriisien kohdalla vastauksena on vertailuja elementti elementiltä. |
|
|
Kokonaisluku1
Vertaa kahta reaalikokonaislukua bitti bitiltä Kokonaisluvut voi syöttää minkä tahansa luvun kantalukuna. Binaarisen syötteen edelle tulee merkitä etumerkki 0b ja heksadesimaalisen syötteen edelle 0h. Jos etumerkkiä ei ole, kokonaislukuja käsitellään desimaalilukuina (kantaluku 10). |
|
|
Katalogi > |
|
|
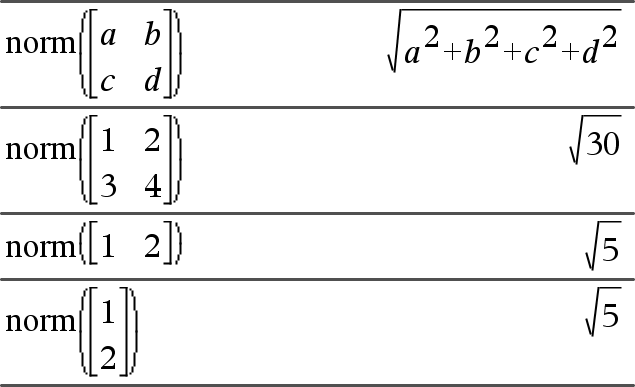
norm(Matriisi)Þlauseke norm(Vektori)Þlauseke Laskee Frobeniusin normin. |
|
|
Katalogi > |
|
|
normalLine(Laus1,Muutt,Piste)Þlauseke normalLine(Laus1,Muutt=Piste)Þlauseke Määrittää normaalisuoran Laus1:n kuvaamasta käyrästä pisteessä, joka on määritetty kohtaan Muutt=Piste. Varmista, että riippumatonta muuttujaa ei ole määritetty. Esimerkiksi, jos f1(x):=5 ja x:=3, tällöin normalLine(f1(x),x,2) antaa vastauksen “epätosi”. |
|
|
Katalogi > |
|
|
normCdf(alaraja,yläraja[,m[,s]])Þluku, jos yläraja ja alaraja ovat lukuja, lista, jos alaraja ja yläraja ovat listoja Laskee normaalijakauman todennäköisyyden alarajan ja ylärajan välillä määritetylle m:lle (oletus=0) ja s:lle (oletus=1). Kun P(X { yläraja), aseta alaraja = .ˆ. |
|
|
Katalogi > |
|
|
normPdf(XArvo[,m,s])Þluku, jos XArvo on luku, lista, jos XArvo on lista Laskee normaalijakauman pistetodennäköisyysfunktion määritetyssä XArvossa määritetylle m:lle ja s:lle. |
|
|
Katalogi > |
|
|
not BoolenLausÞBoolen lauseke Määrittää totuusarvon tosi, epätosi tai argumentin sievennetyn muodon. |
|
|
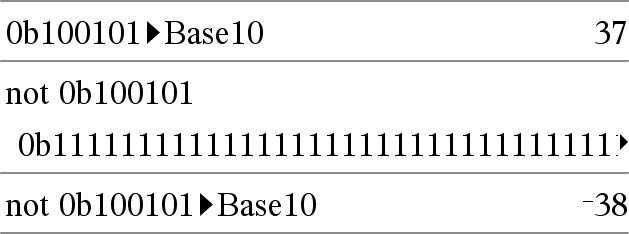
not Kokonaisluku1Þkokonaisluku Laskee reaalikokonaisluvun ykkösen komplementin. Sisäisesti Kokonaisluku1 muunnetaan etumerkilliseksi, 64-bittiseksi binaariluvuksi. Jokaisen bitin arvo vaihtuu (0:sta tulee 1 ja päin vastoin) ykkösen komplementille. Tulokset näytetään kantalukutilan mukaisesti. Voit syöttää kokonaisluvun minkä tahansa luvun kantalukuna. Binaarisen syötteen edelle tulee merkitä etumerkki 0b ja heksadesimaalisen syötteen edelle 0h. Ilman etuliitettä kokonaislukua käsitellään desimaalilukuna (kantaluku 10). Jos syötät desimaalikokonaisluvun, joka on etumerkillisen, 64 bitin binaarimuodon lukualueen ulkopuolella, laskin käyttää symmetristä modulo-operaatiota, jotta arvo saadaan oikealle alueelle. Lisätietoja, katso 4Base2, täältä. |
Heksadesimaalisessa kantalukutilassa:
Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8. Huomaa: Binaarisessa syötteessä voi olla korkeintaan 64 numeroa (etuliitettä 0b ei lasketa). Heksadesimaalisessa syötteessä voi olla korkeintaan 16 numeroa. |
|
Katalogi > |
|
|
nPr(Laus1, Laus2)Þlauseke Kokonaisluvulle Laus1 ja Laus2 sekä Laus1 | Laus2 | 0, nPr() on Laus1:n asioiden permutaatioiden lukumäärä, joita otetaan Laus2:n verran kerrallaan. Kumpikin argumentti voi olla kokonaisluku tai symbolinen lauseke. nPr(Laus, 0)Þ1 nPr(Laus, negKokonaisluku)Þ 1/((Laus+1)·(Laus+2)... (lausekeNnegKokonaisluku)) nPr(Laus, posKokonaisluku)Þ Laus·(LausN1)... (LausNposKokonaisluku+1) nPr(Laus, eiKokonaisluku)ÞLaus! / (LausNeiKokonaisluku)!
|
|
|
nPr(Lista1, List2)Þlista Luo listan permutaatioista kahden listan sisältämiin vastaaviin elementtipareihin perustuen. Argumenttien on oltava samankokoisia listoja. |
|
|
nPr(Matriisi1, Matriisi2)Þmatriisi Luo matriisin permutaatioista kahden matriisin sisältämiin vastaaviin elementtipareihin perustuen. Argumenttien on oltava samankokoisia matriiseja. |
|
|
Katalogi > |
|
|
npv(Korkoprosentti,CFO,CFLista[,CFFrekv]) Talouslaskentatoiminto, joka laskee nettonykyarvon; tulevien ja poistuvien kassavirtojen nykyisten arvojen summan. Jos npv:n tulos on positiivinen, investointi on kannattava. Korkoprosentti on prosentti, jolla kassavirtoja (rahan kustannusta) vähennetään yhden jakson aikana. CF0 on alkuperäinen kassavirta aikana 0; arvon on oltava kokonaisluku. CFLista on lista kassavirtamääristä ensimmäisen kassavirran CF0 jälkeen. CFFrekv on lista, jossa jokainen elementti määrittää esiintymisfrekvenssin ryhmitetylle (peräkkäiselle) kassavirtamäärälle, joka on CFListan vastaava elementti. Oletusarvo on 1; jos syötät arvoja, niiden on oltava positiivisia kokonaislukuja < 10,000. |
|
|
Katalogi > |
|
|
nSolve(Yhtälö,Muutt[=Arvaus])Þluku tai virhe_merkkijono nSolve(Yhtälö,Muutt[=Arvaus],alaraja) nSolve(Yhtälö,Muutt[=Arvaus],alaraja,yläraja) Þluku tai virhe_merkkijono nSolve(Yhtälö,Muutt[=Arvaus]) | alaraja{Muutt{yläraja Etsii iteratiivisesti yhtä likimääräistä numeerista ratkaisua Yhtälön yhdelle muuttujalle. Määritä muuttuja seuraavasti: muuttuja
Esimerkiksi x kelpaa ja samoin x=3. |
Huomaa: Jos ratkaisuja on useita, voit yrittää löytää tietyn ratkaisun käyttämällä apuna arvausta. |
|
nSolve() yrittää määrittää joko yhden pisteen, jossa jäännös on nolla, tai kaksi toisiaan suhteellisen lähellä olevaa pistettä, jossa jäännöksen etumerkki on vastakkainen ja jäännöksen magnitudi ei ole liian suuri. Jos funktio ei pysty määrittämään tätä kohtuullisella otospisteiden määrällä, se antaa vastauksena merkkijonon “no solution found” (yhtään ratkaisua ei löydy).
|
|