Catalogue > 
zeros(Expr, Var)Þliste
zeros(Expr, Var=Init)Þliste
Donne la liste des valeurs réelles possibles de Var avec lesquelles Expr=0. Pour y parvenir, zeros() calcule exp4list(solve(Expr=0,Var),Var).
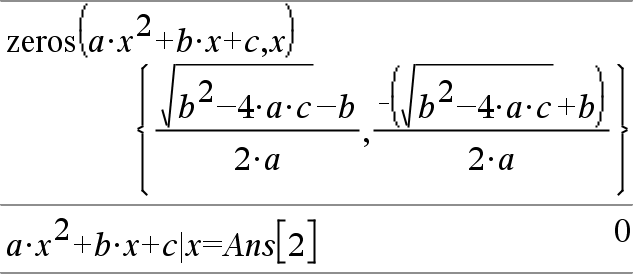
Dans certains cas, la nature du résultat de zeros() est plus satisfaisante que celle de solve(). Toutefois, la nature du résultat de zeros() ne permet pas d'exprimer des solutions implicites, des solutions nécessitant des inéquations ou des solutions qui n'impliquent pas Var.
Remarque : voir aussi cSolve(), cZeros() et solve().
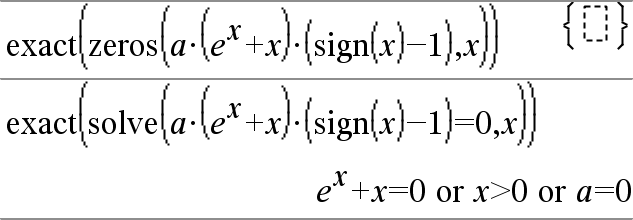
zeros({Expr1, Expr2}, {VarOuInit1, VarOuInit2 [, … ]})Þmatrice
Donne les zéros réels possibles du système d'expressions algébriques, où chaque VarOuInit spécifie une inconnue dont vous recherchez la valeur.
Vous pouvez également spécifier une condition initiale pour les variables. Chaque VarOuInit doit utiliser le format suivant :
variable
– ou –
variable = nombre réel ou nonréel
Par exemple, x est autorisé, de même que x=3.
Si toutes les expressions sont polynomiales et si vous NE spécifiez PAS de condition initiale, zeros() utilise la méthode d'élimination lexicale Gröbner/Buchberger pour tenter de trouver tous les zéros réels.
Par exemple, si vous avez un cercle de rayon r centré à l'origine et un autre cercle de rayon r centré, au point où le premier cercle coupe l'axe des x positifs. Utilisez zeros() pour trouver les intersections.
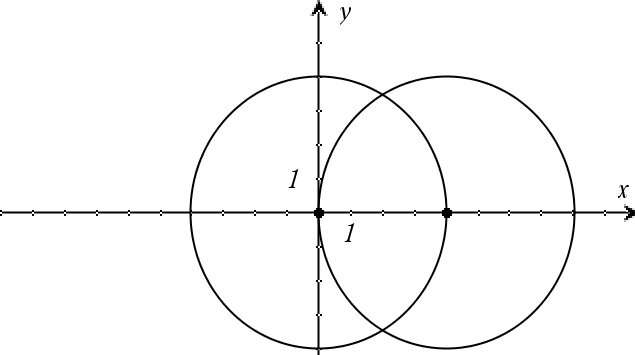
Comme l'illustre r dans l'exemple ci-contre, des expressions polynomiales simultanées peuvent avoir des variables supplémentaires sans valeur assignée, mais représenter des valeurs auxquelles on peut affecter par la suite des valeurs numériques.
Chaque ligne de la matrice résultante représente un n_uplet, l'ordre des composants étant identique à celui de la liste VarOuInit. Pour extraire une ligne, indexez la matrice par [ligne].
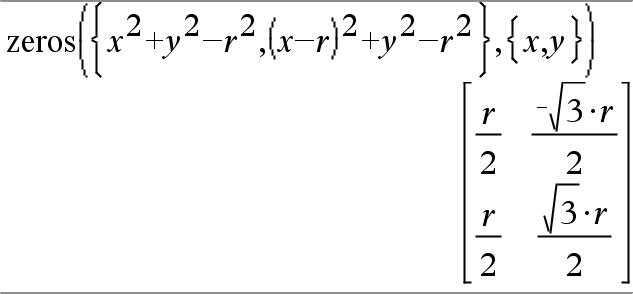
Extraction ligne 2 :

Vous pouvez également utiliser des inconnues qui n'apparaissent pas dans les expressions. Par exemple, vous pouvez utiliser z comme inconnue pour développer l'exemple précédent et avoir deux cylindres parallèles sécants de rayon r. La solution des cylindres montre comment des groupes de zéros peuvent contenir des constantes arbitraires de type ck, où k est un suffixe entier compris entre 1 et 255.
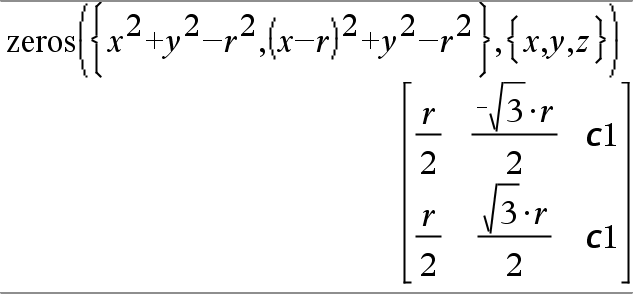
Pour les systèmes d'équations polynomiaux, le temps de calcul et l'utilisation de la mémoire peuvent considérablement varier en fonction de l'ordre dans lequel les inconnues sont spécifiées. Si votre choix initial ne vous satisfait pas pour ces raisons, vous pouvez modifier l'ordre des variables dans les expressions et/ou la liste VarOuInit.
Si vous choisissez de ne pas spécifier de condition et s'il l'une des expressions n'est pas polynomiale dans l'une des variables, mais que toutes les expressions sont linéaires par rapport à toutes les inconnues, zeros() utilise l'élimination gaussienne pour tenter de trouver tous les zéros réels.
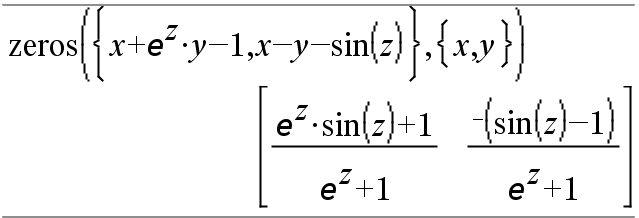
Si un système d'équations n'est pas polynomial dans toutes ses variables ni linéaire par rapport à ses inconnues, zeros() cherche au moins un zéro en utilisant une méthode itérative approchée. Pour cela, le nombre d'inconnues doit être égal au nombre d'expressions et toutes les autres variables contenues dans les expressions doivent pouvoir être évaluées à des nombres.
Chaque inconnue commence à sa valeur supposée, si elle existe ; sinon, la valeur de départ est 0.0.
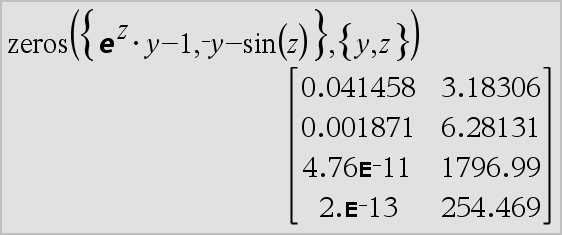
Utilisez des valeurs initiales pour rechercher des zéros supplémentaires, un par un. Pour assurer une convergence correcte, une valeur initiale doit être relativement proche d'un zéro.