Example: Calculate a distribution to fit the Normal Pdf distribution model.

1.

Click the column formula cell (second cell from the top) in column A.

2.

Click Statistics > Distributions > Normal Pdf to choose the Distribution model.

The Normal Pdf dialogue box opens and displays fields for typing or selecting the arguments for the calculation.

3.

Press Tab as necessary to move from field to field and provide each argument. You can type values, or select them from the drop-down list:

-

X Value: Click the drop-down arrow to choose any list in the problem to provide the x values for the calculation.

-

Mean: Type a value for the mean or click the drop-down arrow to choose a variable that contains the mean.

-

Standard Deviation: Type a value for the standard deviation or choose a variable that contains the standard deviation.

4.

Click the Draw tick box to see the distribution plotted in Data & Statistics.

Note: The Draw option is not available for all distributions.

5.

Click OK.

Lists & Spreadsheet inserts two columns: one containing the names of the results, and one containing the corresponding values. The results are plotted in Data & Statistics.

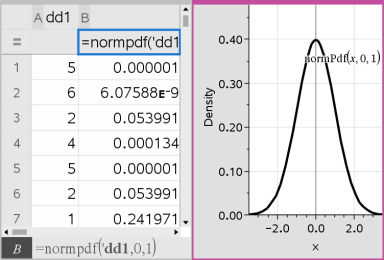
Note: The results are linked to the source data. For example, you can change a value in Column A, and the equation updates automatically.

 

The following distributions are available from the Lists & Spreadsheet application. For more information regarding these functions, see the TI-Nspire™ Reference Guide.

•

To return a single distribution result based on a single value, type the function in a single cell.

•

To return a list of distribution results based on a list of values, type the function in a column formula cell. In this case, you specify a list (column) that contains the values. For each value in the list, the distribution returns a corresponding result.

Note: For distribution functions that support the draw option (normPdf, t Pdf, χ² Pdf, and F Pdf), the option is available only if you type the distribution function in a formula cell.

Normal Pdf (normPdf)

Computes the probability density function (Pdf) for the normal distribution at a specified x value. The defaults are mean μ=0 and standard deviation σ=1. The probability density function (Pdf) is:

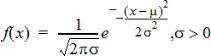
This distribution is used to determine the probability of the occurrence of a certain value in a normal distribution. The draw option is available when Normal Pdf is invoked from a formula cell.

When you access distributions from the formula cell, you must select a valid list from the drop-down list to avoid unexpected results. If accessed from a cell, you must specify a number for the x-value. The distribution returns the probability that the value you specify will occur.

Normal Cdf (normCdf)

Computes the normal distribution probability between Lower Bound and Upper Bound for the specified mean, μ (default=0) and the standard deviation, s (default=1). You can click the Draw (Shade area) box to shade the area between the lower and upper bounds. Changes to the initial Lower Bound and Upper Bound automatically update the distribution.

This distribution is useful in determining the probability of an occurrence of any value between the lower and upper bounds in the normal distribution. It is equivalent to finding the area under the specified normal curve between the bounds.

Inverse Normal (invNorm)

Computes the inverse cumulative normal distribution function for a given area under the normal distribution curve specified by mean, μ and standard deviation, s.

This distribution is useful in determining the x-value of data in the area from 0 to x<1 when the percentile is known.

t Pdf (tPdf)

Computes the probability density function (Pdf) for the tdistribution at a specified x value. df (degrees of freedom) must be 0. The probability density function (Pdf) is:

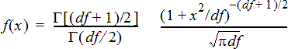
This distribution is useful in determining the probability of the occurrence of a value when the population standard deviation is not known and the sample size is small. The draw option is available when tPdf is invoked from a formula cell.

t Cdf (tCdf)

Computes the Student-t distribution probability between Lower Bound and Upper Bound for the specified df (degrees of freedom). You can click the Draw (Shade area) box to shade the area between the bounds. Changes to the initial Lower Bound and Upper Bound automatically update the distribution.

This distribution is useful in determining the probability of the occurrence of a value within an interval defined by the lower and upper bound for a normally distributed population when the population standard deviation is not known.

Inverse t (invt)

Computes the inverse cumulative t-distribution probability function specified by Degrees of Freedom, df, for a given area under the curve.

This distribution is useful in determining the probability of an occurrence of data in the area from 0 to x<1. This function is used when the population mean and/or population standard deviation is not known.

c2 Pdf (c2 Pdf())

Computes the probability density function (Pdf) for the c2 (chi-square) distribution at a specified x value. df (degrees of freedom) must be an integer > 0. The probability density function (Pdf) is:

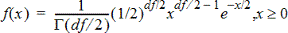
This distribution is useful in determining the probability of the occurrence of a given value from a population with a c2 distribution. The draw option is available when c2 Pdf is invoked from a formula cell.

c2 Cdf (c2 Cdf())

Computes the c2 (chi-square) distribution probability between lowBound and upBound for the specified df (degrees of freedom). You can click the Draw Shade area box to shade the area between the lower and upper bounds. Changes to the initial lowBound and upBound automatically update the distribution.

This distribution is useful in determining the probability of the occurrence of value within given boundaries of a population with a c2 distribution.

F Pdf (F Pdf())

Computes the probability density function (Pdf) for the F distribution at a specified x value. numerator df (degrees of freedom) and denominator df must be integers > 0. The probability density function (Pdf) is:

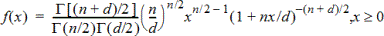
where

n = numerator degrees of freedom d = denominator degrees of freedom

This distribution is useful in determining the probability that two samples have the same variance. The draw option is available when F Pdf is invoked from a formula cell.

F Cdf (F Cdf())

Computes the F distribution probability between lowBound and upBound for the specified dfnumer (degrees of freedom) and dfDenom. You can click the Draw (Shade area) box to shade the area between the lower and upper bounds. Changes to the initial lowBound and upBound automatically update the distribution.

This distribution is useful in determining the probability that a single observation falls within the range between the lower bound and upper bound.

Binomial Pdf (binomPdf())

Computes a probability at x for the discrete binomial distribution with the specified numtrials and probability of success (p) on each trial. The x parameter can be an integer or a list of integers. 0{p{1 must be true. numtrials must be an integer > 0. If you do not specify x, a list of probabilities from 0 to numtrials is returned. The probability density function (Pdf) is:

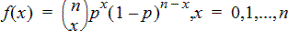
where n = numtrials

This distribution is useful in determining the probability of success in a success/failure trial, at trial n. For example, you could use this distribution to predict the probability of getting heads in a coin toss on the fifth toss.

Binomial Cdf (binomCdf())

Computes a cumulative probability for the discrete binomial distribution with n number of trials and probability p of success on each trial.

This distribution is useful in determining the probability of a success on one trial before all trials are completed. For example, if heads is a successful coin toss and you plan to toss the coin 10 times, this distribution would predict the chance of obtaining heads at least once in the 10 tosses.

Inverse Binomial (invBinom())

Given the number of trials (NumTrials) and the probability of success of each trial (Prob), this function returns the minimum number of successes, k, such that the cumulative probability of k successes is greater than or equal to the given cumulative probability (CumulativeProb).

Inverse Binomial with respect to N (invBinomN())

Given the probability of success of each trial (Prob), and the number of successes (NumSuccess), this function returns the minimum number of trials, N, such that the cumulative probability of x successes is less than or equal to the given cumulative probability (CumulativeProb).

Poisson Pdf (poissPdf())

Computes a probability at x for the discrete Poisson distribution with the specified mean, μ, which must be a real number > 0. x can be an integer or a list of integers. The probability density function (Pdf) is:

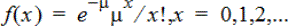
This distribution is useful in determining the probability of obtaining a certain number of successes before a trial begins. For example, you could use this calculation to predict the number of heads that would occur in eight tosses of a coin.

Poisson Cdf (poissCdf())

Computes a cumulative probability for the discrete Poisson distribution with specified mean, x.

This distribution is useful in determining the probability that a certain number of successes occur between the upper and lower bounds of a trial. For example, you could use this calculation to predict the number of heads displayed between coin toss No.3 and toss No.8.

Geometric Pdf (geomPdf())

Computes a probability at x, the number of the trial on which the first success occurs, for the discrete geometric distribution with the specified probability of success p. 0{p{1 must be true. x can be an integer or a list of integers. The probability density function (Pdf) is:

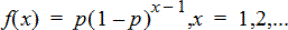
This distribution is useful in determining the likeliest number of trials before a success is obtained. For example, you could use this calculation to predict the number of coin tosses that would be made before a heads resulted.

Geometric Cdf (geomCdf())

Computes a cumulative geometric probability from lowBound to upBound with the specified probability of success, p.

This distribution is useful in determining the probability associated with the first success occurring during trials 1 through n. For example, you could use this calculation to determine the probability that heads display on toss No.1, No.2, No.3, ..., No.n.