Graphing Relations

Relation graphing is available on Graphs pages and in the Analytic Window of Geometry pages.

You can define relations using ≤, <, =, > or ≥. The inequality operator (≠) is not supported in relation graphing.

Relation type	Examples
Equations and inequalities equivalent to y = f(x)	• y = sqrt(x) • y-sqrt(x) = 1/2 • -2*y-sqrt(x) = 1/2 • y-sqrt(x) ≥ 1/2 • -2*y-sqrt(x) ≥ 1/2
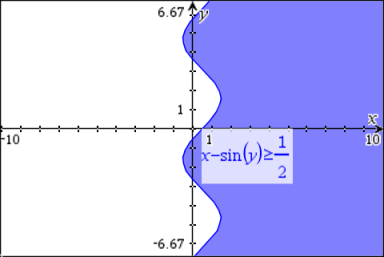
Equations and inequalities equivalent to x = g(y)	• x = sin(y) • x-sin(y) = 1/2 • x-sin(y) ≥ 1/2
Polynomial equations and inequalities	• x^2+y^2 = 5 • x^2-y^2 ≥ 1/2+y • x3+y3-6*x*y=0
The above relations on domains restricted by rectangles	• y=sin(x) and -2π<x≤2π • y≤x2|y≥-2 and 0≤x≤3 • {x2+y2≤3, y≥0 and x≤0

Note: Restrictions imposed by an active Press-to-Test session may limit the types of relations you can graph.

To Graph a Relation:

1.

From the Graph Entry/Edit menu, select Relation.

2.

Type an expression for the relation.

3.

Press Enter to graph the relation.

Tips for Graphing Relations

▶

You can quickly define a relation from the Function entry line. Position the cursor to the immediate right of the = sign, and then press the Backspace key. A small menu appears with the relation operators and a Relation option. Choosing from the menu places the cursor in the Relation entry line.

▶

You can type a relation as text on a Graphs page and then drag the text object over either axis. The relation is graphed and added to the relation history.

Warning and Error Message

Error Condition	Additional Information
Relation input not supported	Relation input not supported Note: The following relation inputs are supported: • Relations using ≤, <, =, >, or ≥. • Polynomial relations in x and y • Relations equivalent to y=f(x) or x=g(y) or corresponding inequalities • The above relations on domains restricted by rectangles
Domain Restrictions not supported for certain classes of relations equivalent to y=f(x) or x=g(y) or corresponding inequalities.	• Relations equivalent to y=f(x) and corresponding inequalities can only have constraints on x • For example: y=√(x) and 0≤x≤1 will work but y=√(x) and 0≤y≤1 will not • Relations equivalent to x=g(y) and corresponding inequalities can only have constraints on y • For example: x=sin(y)|−1≤y≤1 will work but x=sin(y)|−1≤x≤1 will not