Menus/Itens de menu
Descrição
Definições de cônicas (Prima z)
Tipo
Selecionar o modo da calculadora
FUNC: Função representa graficamente funções, em que Y é uma função de X.
PAR: Paramétrica representa graficamente relações, em que X e Y são funções de T.
POL: Polar representa graficamente funções, em que R é uma função de
Definições da janela
Selecione AUTO para que as janelas mudem automaticamente.
Selecione MAN para que possa mudar manualmente as definições da janela.
Esc
Voltar ao ecrã anterior.
Menu principal
Circunferência
Uma circunferência é um conjunto de pontos num plano, cuja distância a um ponto fixo é constante. O ponto fixo é o centro da circunferência; a distância constante é o raio.
Elipse
Uma elipse é um conjunto de pontos, cujas distâncias a dois pontos fixos no plano têm uma soma constante. Os dois pontos fixos são os focos da elipse. A reta definida pelos focos de uma elipse é o eixo focal da elipse. O ponto médio dos focos é o centro. Os pontos de interseção do eixo focal com a elipse são vértices da elipse.
Hipérbole
Uma hipérbole é um conjunto de pontos num plano, cujas distâncias de dois pontos fixos no plano têm uma diferença constante. Os dois pontos fixos são os focos da hipérbole. A reta definida pelos focos de uma hipérbole é o eixo focal. O ponto no eixo a meio caminho entre os focos é o centro da hipérbole. Os pontos de interseção do eixo focal com a hipérbole são os vértices.
Parábola
O conjunto de todos os pontos de um plano equidistantes de um determinado ponto fixo e de uma determinada reta fixa no mesmo plano é uma parábola. O ponto fixo é o foco da parábola. A reta fixa é a diretriz. O ponto onde o eixo focal interseta a parábola é o vértice.
Info
Apresenta o ecrã de informação que contém o número de versão da aplicação.
Sair
Selecione SAIR para sair da representação gráfica de cónicas.
Esc
Selecione ESC para ir um ecrã para trás.
Menu Circunferência
(X-H)2 + (Y-K)2 = R2
No modo FUNC, selecione esta equação e introduza H, K e R.
AX2 + AY2 + BX + CY+ D = 0
No modo FUNC, selecione esta equação e introduza A, B, C e D.
X=Rcos(T)+H
Y=Rsin(T)+K
No modo PAR, selecione esta equação paramétrica e introduza H, K e R.
1:R+2Acos(0)
No modo POL, selecione esta equação polar e introduza A.
2:R=2Asin(0)
No modo POL, selecione esta equação polar e introduza A.
3:A2=B2+R2-2BRcos(0-b)
Selecione esta equação polar e introduza A, B e b.
[GRAPH]
Selecione para representar graficamente a equação.
ƒ \
Apresenta o centro e o raio.
r
Trace a circunferência.
Menu Elipse
1: 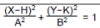
No modo FUNC, selecione esta equação e introduza A, B, H e K.
2: 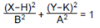
No modo FUNC, selecione esta equação e introduza A, B, H e K.
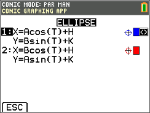
No modo PAR, selecione esta equação paramétrica e introduza A, B, H e K.
No modo PAR, selecione esta equação paramétrica e introduza A, B, H e K.
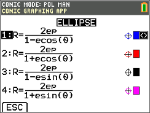
No modo POL, selecione esta equação polar e introduza e e p.
No modo POL, selecione esta equação polar e introduza e e p.
No modo POL, selecione esta equação polar e introduza e e p.
No modo POL, selecione esta equação polar e introduza e e p.
[GRAPH]
Selecione para representar graficamente a equação.
ƒ \
Apresenta o centro e os focos.
r ¤
Trace a órbita.
Menu Hipérbole
1: 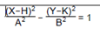
No modo FUNC, selecione esta equação de função e introduza A, B, H e K.
2: 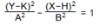
No modo FUNC, selecione esta equação de função e introduza A, B, H e K.
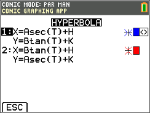
No modo PAR, selecione esta equação paramétrica e introduza A, B, H e K.
No modo PAR, selecione esta equação paramétrica e introduza A, B, H e K.
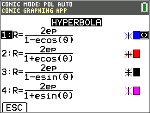
No modo POL, selecione esta equação polar e introduza e e p.
No modo POL, selecione esta equação polar e introduza e e p.
No modo POL, selecione esta equação polar e introduza e e p.
No modo POL, selecione esta equação polar e introduza e e p.
[GRAPH]
Selecione para representar graficamente a equação.
ƒ \
Apresenta o centro, os vértices, os focos e o declive das assíntotas.
r ¤
Trace a hipérbole.
Menu Parábole
1: (Y-K)2 = 4P(X-H)
No modo FUNC, selecione esta equação de função e introduza A, B, H e K.
2: (X-H)2 = 4P(Y-K)
No modo FUNC, selecione esta equação de função e introduza A, B, H e K.
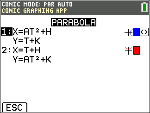
No modo PAR, selecione esta equação paramétrica e introduza A, H e K.
No modo PAR, selecione esta equação paramétrica e introduza A, H e K.
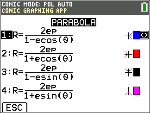
No modo POL, selecione esta equação polar e introduza e e p.
No modo POL, selecione esta equação polar e introduza e e p.
No modo POL, selecione esta equação polar e introduza e e p.
No modo POL, selecione esta equação polar e introduza e e p.
[GRAPH]
Selecione para representar graficamente a equação.
ƒ \
Apresenta o vértice, o foco e a diretriz.
r ¤
Trace a trajetória.