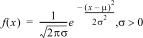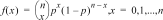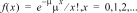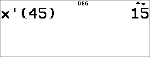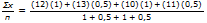Statistica, regressioni e distribuzioni
v % u
v consente di immettere e modificare le liste di dati. (vedere la sezione Editor di dati).
% u visualizza il menu , che ha le seguenti opzioni.
Nota:
|
•
|
Le regressioni memorizzano le informazioni di regressione, insieme ai valori statistici 2-Var per i dati, in StatVars (voce menu 1). |
|
•
|
Una regressione può essere memorizzata in f(x) o g(x). I coefficienti di regressione vengono visualizzati con la massima precisione. |
Nota importante sui risultati: Molte delle equazioni di regressione condividono le stesse variabili , , e . Se si effettua qualsiasi calcolo di regressione, il calcolo di regressione e i valori statistici 2-Var per tali dati vengono memorizzati nel menu fino al prossimo calcolo statistico o di regressione. I risultati devono essere interpretati in base al tipo di calcolo statistico o di regressione eseguito per ultimo. Quale ausilio per interpretare correttamente, la barra del titolo ricorda quale calcolo è stato eseguito per ultimo.
|
1:StatVars
|
Visualizza un menu delle variabili del risultato statistico calcolato per ultimo. Utilizzare $ e # per individuare la variabile desiderata e premere < per selezionarla. Se si seleziona questa opzione prima di calcolare 1-Var stats, 2-Var stats o qualsiasi regressione, compare un promemoria.
|
|
2:1-VAR STATS
|
Analizza i dati statistici da 1 insieme di dati con 1 variabile misurata, x. Possono essere compresi dati di frequenza.
|
|
3:2-VAR STATS
|
Analizza dati appaiati di 2 insiemi di dati con 2 variabili misurate: x, la variabile indipendente, e y, la variabile dipendente. Possono essere compresi dati di frequenza.
Nota: 2-Var Stats calcola anche una regressione lineare e inserisce i risultati della regressione lineare. Visualizza i valori di (pendenza) e (intercetta y); visualizza anche i valori di 2 e .
|
|
4:LinReg ax+b
|
Adatta l'equazione modello y=ax+b ai dati mediante un adattamento con il metodo dei minimi quadrati per almeno due punti dati. Visualizza i valori di (pendenza) e (intercetta y); visualizza anche i valori di 2 e .
|
|
5:PropReg ax
|
Adatta l'equazione modello y=ax ai dati mediante adattamento con il metodo dei minimi quadrati per almeno un punto dati. Visualizza il valore di . Supporta dati che formano a una linea verticale con l'eccezzione di tutti i dati 0.
|
|
6:RecipReg a/x+b
|
Adatta l'equazione modello y=a/x+b ai dati mediante adattamento con il metodo dei minimi quadrati su dati linearizzati per almeno due punti dati. Visualizza i valori di e ; visualizza anche i valori di 2 e .
|
|
7:QuadraticReg
|
Adatta il polinomio di secondo grado y=ax2+bx+c ai dati. Visualizza i valori di , e ; inoltre visualizza un valore per 2. Per tre punti dati, l'equazione è un adattamento polinomiale; per quattro o più punti dati è una regressione polinomiale. Sono necessari almeno tre punti dati.
|
|
8:CubicReg
|
Adatta il polinomio di terzo grado y=ax3+bx2+cx+d ai dati. Visualizza i valori di , , e ; inoltre visualizza un valore per 2. Per quattro punti dati, l'equazione è un adattamento polinomiale; per cinque o più punti dati è una regressione polinomiale. Sono necessari almeno quattro punti.
|
|
9:LnReg a+blnx
|
Adatta l'equazione modello y=a+b ln(x) ai dati utilizzando un adattamento con il metodo dei minimi quadrati e valori trasformati ln(x) e y. Visualizza i valori di e ; visualizza anche i valori di 2 e .
|
|
:PwrReg ax^b
|
Adatta l'equazione modello y=axb ai dati utilizzando un adattamento con il metodo dei minimi quadrati e valori trasformati ln(x) e ln(y). Visualizza i valori di e ; visualizza anche i valori di 2 e .
|
|
:ExpReg ab^x
|
Adatta l'equazione modello y=abx ai dati utilizzando un adattamento con il metodo dei minimi quadrati e valori trasformati x e ln(y). Visualizza i valori di e ; visualizza anche i valori di 2 e .
|
|
:expReg ae^(bx)
|
Adatta l'equazione modello y=a e^(bx) ai dati mediante adattamento con il metodo dei minimi quadrati su dati linearizzati per almeno due punti dati. Visualizza i valori di e ; visualizza anche i valori di 2 e .
|
% u " visualizza il menu , che contiene le seguenti funzioni distribuzione:
|
1:Normalpdf
|
Calcola la funzione della densità di probabilità (pdf) per la distribuzione normale in corrispondenza di un valore x. I valori predefiniti sono media mu=0 e deviazione standard sigma=1. La funzione della densità di probabilità (pdf) è:
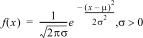
|
|
2:Normalcdf
|
Calcola la probabilità di distribuzione normale tra LOWERbnd e UPPERbnd per la media mu e la deviazione standard sigma specificate. I valori predefiniti sono mu=0; sigma=1; con LOWERbnd = M1E99 e UPPERbnd = 1E99.
Nota: L'intervallo di valori da M1E99 a 1E99 rappresenta da Minfinito a infinito.
|
|
3:invNormal
|
Calcola la funzione della distribuzione normale cumulativa inversa per una data area sottesa dalla curva della distribuzione normale specificata da media mu e deviazione standard sigma. Calcola il valore x associato a un'area a sinistra del valore x. 0 { area { 1 deve essere vero. I valori predefiniti sono area=1, mu=0 e sigma=1.
|
|
4:Binomialpdf
|
Calcola una probabilità in corrispondenza di x per la distribuzione binomiale discreta con il numtrials (numero di prove) e la probabilità di successo (p) specificati per ciascuna prova. x è un numero intero non negativo e può essere immesso con le opzioni di immissione SINGLE (singola), LIST (elenco) di immissioni o ALL (viene restituito l'elenco di probabilità da 0 a numtrials). 0 { p { 1 deve essere vero. La funzione della densità di probabilità () è:
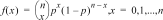
|
|
5:Binomialcdf
|
Calcola una probabilità cumulativa in corrispondenza di x per la distribuzione binomiale discreta con il numtrials e la probabilità di successo (p) specificati per ciascuna prova. x può essere intero non negativo e può essere immesso con le opzioni di SINGLE, LIST o ALL (viene restituito un elenco di probabilità cumulative). 0 { p { 1 deve essere vero.
|
|
6:Poissonpdf
|
Calcola una probabilità in corrispondenza di x per la distribuzione di Poisson discreta con la media mu (m) specificata, che deve essere un numero reale > 0. x può essere un numero intero non negativo (SINGLE) o un elenco di numeri interi (LIST). Il valore predefinito è mu=1. La funzione della densità di probabilità () è:
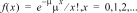
|
|
7:Poissoncdf
|
Calcola una probabilità cumulativa in corrispondenza di x per la distribuzione di Poisson discreta con la media mu specificata, che deve essere un numero reale > 0. x può essere un numero intero non negativo (SINGLE) o un elenco di numeri interi (LIST). Il valore predefinito è mu=1.
|
Risultati statistici
|
|
1-Var
|
Numero di punti dati x o (x,y).
|
|
v
|
Entrambe
|
Media di tutti i valori di x.
|
|
w
|
2-Var
|
Media di tutti i valori di y.
|
|
|
Entrambe
|
Deviazione standard dei campioni di x.
|
|
|
2-Var
|
Deviazione standard dei campioni di y.
|
|
s
|
Entrambe
|
Deviazione standard della popolazione x.
|
|
s
|
2-Var
|
Deviazione standard della popolazione di y.
|
|
G o G2
|
Entrambe
|
Sommatoria di tutti i valori di x o x2.
|
|
G o G2
|
2-Var
|
Sommatoria di tutti i valori di y o y2.
|
|
G
|
2-Var
|
Sommatoria di (xQy) per tutte le coppie xy.
|
|
|
2-Var
|
Pendenza della regressione lineare.
|
|
|
2-Var
|
Intercetta-y della regressione lineare.
|
|
2 o
|
2-Var
|
Coefficiente di correlazione.
|
|
¢
|
2-Var
|
Utilizza a e b per calcolare il valore previsto di x quando si immette un valore di y.
|
|
¢
|
2-Var
|
Utilizza a e b per calcolare il valore previsto di y quando si immette un valore di x.
|
|
o
|
Entrambe
|
Minimo o massimo dei valori di x.
|
|
|
1-Var
|
Mediana degli elementi tra minX e Med (1° quartile).
|
|
|
1-Var
|
Mediana di tutti i punti dati.
|
|
|
1-Var
|
Mediana degli elementi tra Med e maxX (3° quartile).
|
|
o
|
2-Var
|
Minimo massimo dei valori di y.
|
Per definire i punti dei dati statistici:
|
1.
|
Immettere i dati in L1, L2 o L3 (vedere la sezione Editor di dati). |
Nota: Sono validi gli elementi di frequenza non interi. Ciò è utile quando si immettono frequenze espresse come percentuali o parti la cui somma è 1. Tuttavia, la deviazione standard del campione, Sx, non è definita per frequenze non intere e per tale valore viene visualizzato Sx=Error. Tutti gli altri valori statistici vengono visualizzati.
|
2.
|
Premere % u. Selezionare o e premere <. |
|
3.
|
Selezionare L1, L2 o L3 e la frequenza. |
|
4.
|
Premere < per visualizzare il menu delle variabili. |
|
5.
|
Per cancellare i dati, premere v v, selezionare un elenco da cancellare e premere <. |
Esempio 1-Var
Calcolare la media di {45,55,55,55}.
|
Cancella tutti i dati
|
v v $ $ $
|
|
|
Dati
|
<
$ $ $
<
|

|
|
Statistica
|
% s
% u
|

|
|
|
(Seleziona )
$ $
|

|
|
|
<
|

|
|
Variabile statistica
|
<
|

|
|
|
V <
|

|
Esempio 2-Var
Dati: (45,30); (55,25). Trovare: x¢(45).
|
Cancella tutti i dati
|
v v $ $ $
|

|
|
Dati
|
< $ $ " $ $
|

|
|
Statistica
|
% u
|

|
|
|
(Seleziona )
$ $ $
|
|
|
Variabili statistiche
|
< % s
% u
# # # # # #
|
|
|
|
< ) <
|
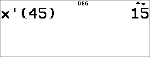
|
³ Problema
Per le sue ultime prove, Anthony ha ottenuto i seguenti punteggi. Alle prove 2 e 4 è stato attribuito un peso di 0,5 e alle prove 1 e 3 è stato attribuito un peso di 1.
|
N. prova
|
1
|
2
|
3
|
4
|
|
Punteggio
|
12
|
13
|
10
|
11
|
|
Peso
|
1
|
0,5
|
1
|
0,5
|
|
1.
|
Trovare il voto medio (media pesata) di Anthony. |
|
2.
|
Che cosa rappresenta il valore di n dato dalla calcolatrice? Che cosa rappresenta il valore di Gx dato dalla calcolatrice? |
Promemoria: La media pesata è
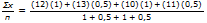
|
3.
|
L'insegnante ha dato ad Anthony 4 punti in più nella prova 4 a causa di un errore di assegnazione del voto. Trovare il nuovo voto medio di Anthony. |
|
v v $ $ $
|

|
|
<
v " $ $ $ $
|

|
|
<
$ $ $ $
" $ $ $
<
|

|
|
% u
|

|
|
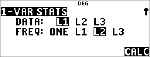
$ " " <
|
|
|
<
|

|
Anthony ha una media (v) di 11,33 (con arrotondamento al centesimo più prossimo).
Sulla calcolatrice, n rappresenta la somma totale dei pesi.
n = 1 + 0,5 + 1 + 0,5.
Gx rappresenta la sommatoria pesata dei suoi punteggi.
(12)(1) + (13)(0,5) + (10)(1) + (11)(0,5) = 34.
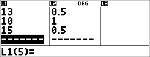
Cambiare l'ultimo punteggio di Anthony da 11 in 15.
|
v $ $ $ <
|
|
|
% u
$ " " < <
|

|
Se l'insegnante aggiunge 4 punti alla prova 4, il voto medio di Anthony è 12.
³ Problema
La tabella sottostante riporta i risultati di una prova di frenata.
|
N. prova
|
1
|
2
|
3
|
4
|
|
Velocità (km/h)
|
33
|
49
|
65
|
79
|
|
Distanza di frenata (m)
|
5,30
|
14,45
|
20,21
|
38,45
|
Utilizzare la relazione tra velocità e distanza di frenata per stimare la distanza di frenata necessaria per un veicolo che procede a 55 km/h.
Un diagramma a dispersione tracciato manualmente di questi punti dati suggerisce una relazione lineare. La calcolatrice utilizza il metodo dei minimi quadrati per trovare la linea di migliore adattamento, y'=ax'+b, per i dati immessi negli elenchi.
|
v v $ $ $
|

|
|
<
$ $ $ $ " $ $ $ <
|
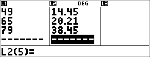
|
|
% s
% u
|

|
|
(Seleziona )
$ $ $
|

|
|
<
|
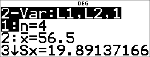
|
|
Premere $ secondo necessità per visualizzare a e b.
|

|
La linea di migliore adattamento, y'=0,67732519x'N18,66637321 modellizza l'andamento lineare dei dati.
|
Premere $ finché non viene evidenziato y'.
|

|
|
< ) <
|

|
Il modello lineare fornisce una distanza di frenata stimata di 18,59 metri per un veicolo che procede a una velocità di 55 km/h.
Esempio di regressione 1
Calcolare una regressione lineare ax+b per i seguenti dati: {1,2,3,4,5}; {5,8,11,14,17}.
|
Cancella tutti i dati
|
v v $ $ $
|

|
|
Dati
|
<
$ $ $ $
$ "
$ $ $ $
<
|

|
|
Regressione
|
% s
% u
$ $ $
|

|
|
|
<
|
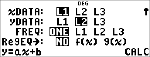
|
|
|
$ $ $ $
<
Premere $ per esaminare tutte le variabili del risultato.
|

|
Esempio di regressione 2
Calcolare la regressione esponenziale per i seguenti dati:
|
•
|
L1 = {0,1,2,3,4}; L2 = {10,14,23,35,48} |
|
•
|
Trovare il valore medio dei dati in L2. |
|
•
|
Confrontare i valori della regressione esponenziale con L2. |
|
Cancella tutti i dati
|
v v
|
|
|
Dati
|
$ $ $ $
$ " $ $ $ $ <
|
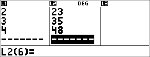
|
|
Regressione
|
% u
# #
|
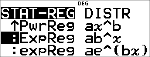
|
|
Salvare l'equazione di regressione
in f(x) nel menu I.
|
< $ $ $ "
<
|
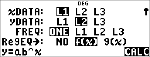
|
|
Equazione di regressione
|
<
|
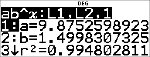
|
|
Trovare il valore medio (y) dei dati in L2 mediante StatVars.
|
% u
(Seleziona )
$ $ $
$ $ $
$ $
|
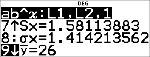
Notare che la barra del titolo ricorda all'utente l'ultimo calcolo statistico o di regressione.
|
|
Esaminare la tabella dei valori dell'equazione di regressione.
|
I
|

|
|
|
< $
<
<
|

|
|
|
< <
|

|
Attenzione: Se a questo punto si calcola 2-Var Stats sui propri dati, le variabili e (insieme con e 2) saranno calcolate come una regressione lineare. Non ricalcolare 2-Var Stats dopo il calcolo di nessun'altra regressione se si desidera preservare i propri coefficienti di regressione (a, b, c, d) e i valori r per il proprio particolare problema nel menu .
Esempio di distribuzione
Calcolare la distribuzione pdf binomiale in corrispondenza dei valori di x {3,6,9} con 20 prove e una probabilità di successo di 0,6. Immettere i valori di x nell'elenco L1, memorizzare i risultati in L2, quindi trovare la sommatoria delle probabilità e memorizzarla nella variabile t.
|
Cancella tutti i dati
|
v v $ $ $
|

|
|
Dati
|
<
$ $
<
|

|
|
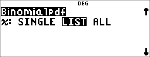
DISTR
|
% u "
$ $ $
|

|
|
|
< "
|
|
|
|
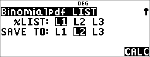
<
$
|

|
|
|
< $ $
|
|
|
|
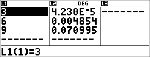
<
|
|
|
|
v ! "
<
|
|
|
|
<
" " " "
< <
|
|