U bent hier: TI-30X Pro MathPrint™ Wetenschappelijke rekenmachine > Math Tools > Oplossers

Oplossers

Numerieke vergelijkings-oplosser

% ‰

% ‰ vraagt u om de vergelijking en de waarden van de variabelen. Daarna kiest u de variabele die u wilt oplossen.

Voorbeeld

Los de volgende vergelijking op voor de variabele b.

Onthoud: Als u al variabelen heeft gedefinieerd zal de oplosser die waarden voor de berekening aannemen.

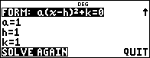
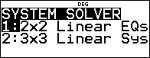
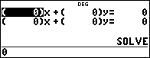
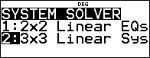
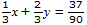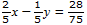Num-solv

% ‰

LINKERKANT

1 P 2 " z F

U 5 z z z

z z " "

RECHTERKANT

6 z U z z

z z z z

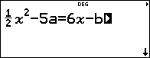
Initiële waarde van de variabele

<

1 P 2 "

 

<

2 P 3 "

 

<

1 P 4 "

Selecteer Oplossingsvariabele

< " "

Oplossingsgrenzen

< $ $

Voer, indien nodig, het interval in waarin u verwacht dat de oplossing ligt als [LOWER,UPPER].

 

<

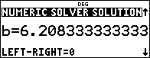
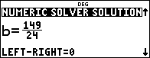
r

Opmerking: LEFT-RIGHT is het verschil tussen het linker- en rechterlid van de vergelijking wanneer deze is uitgewerkt voor de berekende oplossing. Dit verschil geeft aan hoe dicht de oplossing ligt bij het exacte antwoord.

Veelterm-oplosser

% Š

% Š laat u de kwadratische oplosser of de derdemachts-oplosser kiezen. Dan voert u de reële coëfficiënten van de variabelen in en start de oplosser. Oplossingen kunnen reëel of complex zijn.

Voorbeeld voor een kwadratische vergelijking

Onthoud: Als u al variabelen heeft gedefinieerd zal de oplosser die waarden voor de berekening aannemen.

Poly-solv

% Š

Voer coëfficiënten in

<

1

 

$

M 2

 

$

2

<

Oplossingen

<

 

$

 

$

Opmerking: Als u ervoor kiest om de veelterm in
f(x) of g(x) op te slaan, kunt u I gebruiken om de waardetabel te onderzoeken.

 

$ $ $ <

Topvorm (alleen bij kwadratische oplosser)

In de oplossingsschermen van de veeltermoplosser kunt u op r drukken om de getalnotatie van de oplossingen x1, x2 voor kwadratische- of x1, x2 en x3 voor derdemachts-veeltermen te wisselen.

Oplosser voor een stelsel van lineaire vergelijkingen

% ‹

% ‹ lost een stelsel van lineaire vergelijkingen op. U kunt kiezen uit 2×2 of 3×3 stelsels.

Opmerkingen:

• de resultaten voor x, y en z worden automatisch opgeslagen in de variabelen x, y en z.
• Gebruik r om zonodig de resultaten (x, y en z) te wisselen.
• De stelseloplosser vindt een unieke oplossing of oneindige oplossingen in gesloten vorm of hij geeft aan geen oplossing te vinden.

Voorbeeld 2×2 stelsel

Los op:

 

Sys-solv

% ‹

2×2 stelsel

<

Voer vergelijkingen in

1 P 3 < <

2 P 3 <

37 P 90 <

2 P 5 <

U 1 P 5 <

28 P 75 <

Oplossing

<

Wijzig de getalnotatie (indien nodig)

r

 

<

Wijzig de getalnotatie (indien nodig)

r

 

<

Voorbeeld 3×3 stelsel

Los op:

5x – 2y + 3z = -9

4x + 3y + 5z = 4

2x + 4y – 2z = 14

 

Sys-solv

% ‹ $

3×3 stelsel

<

Voer coëfficiënten in

5 < M 2 < 3 < M 9 <

4 < 3 < 5 < 4 <

2 < 4 < M 2 < 14 <

Opmerking: Let erop dat voor 3x3, de eerste vergelijking moet worden ingevoerd als:

5x + M2 + 3z = M9

Oplossing

<

 

<

 

<

 

<

Opmerking: Gebruik r om zonodig de getalnotatie te wisselen.

Voorbeeld van een 3×3 stelsel met oneindige oplossing

Voer het stelsel in

% ‹ 2

1 < 2 < 3 < 4

<

2 < 4 < 6 < 8

<

3 < 6 < 9 < 12

<

Oplossing

<

 

<

 

<

 

<

 

<