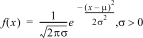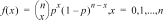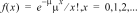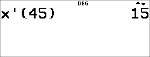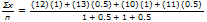Statistiek, regressies en verdelingen
v % u
Met v kunt u de gegevenslijsten invoeren en bewerken. (Zie paragraaf Data Editor.)
% u toont het menu , dat de volgende opties bevat.
Opmerkingen:
|
•
|
Regressies slaan de regressie-informatie op in StatVars (menu item 1), samen met de 2-Var statistische getallen voor de gegevens. |
|
•
|
Een regressie kan worden opgeslagen in f(x) of in g(x). De regressiecoëfficiënten worden in volledige nauwkeurigheid getoond. |
Belangrijke opmerking over de resultaten: Veel van de regressievergelijkingen delen dezelfde variabelen , , en . Als u een regressieberekening uitvoert worden de regressieberekening en de 2-Var statistische maten voor die gegevens opgeslagen in het menu tot de volgende statistische berekening of regressie plaatsvindt. De resultaten dienen te worden geïnterpreteerd rekening houdend met het soort statistische berekening of regressie dat de laatste keer werd uitgevoerd. Om u bij de juiste interpretatie te helpen, toont de bovenste regel welke berekening het laatst was uitgevoerd.
|
1:StatVars
|
Toont een secundair menu met de variabelen van het laatst berekende statistische resultaat. Gebruik $ en # om de gewenste variabele te vinden en druk op < om deze te selecteren. Als u deze optie al selecteert voor het berekenen van 1-Var stats, 2-Var stats of een van de regressies, verschijnt een herinnering.
|
|
2:1-VAR STATS
|
Analyseert statistische gegevens van 1 dataset met 1 gemeten variabele, x. Frequentiegegevens kunnen worden ingevoerd.
|
|
3:2-VAR STATS
|
Analyseert de gegevens-paren van 2 datasets met 2 gemeten variabelen—x, de onafhankelijke variabele, en y, de afhankelijke variabele. Frequentiegegevens kunnen worden ingevoerd.
Opmerking: 2-Var Stats berekent ook een lineaire regressie en slaat die op in de lineaire regressie resultaten. Het toont waarden voor (helling) en (snijpunt met y-as); het toont ook waarden voor 2 en .
|
|
4:LinReg ax+b
|
Past de modelvergelijking y=ax+b toe op de gegevens door het gebruik van de kleinste-kwadraten methode op tenminste twee datapunten. Het toont waarden voor (helling) en (snijpunt met y-as); het toont ook waarden voor 2 en .
|
|
5:PropReg ax
|
Past de modelvergelijking y=ax toe op de gegevens door het gebruik van de kleinste-kwadraten methode op tenminste één datapunt. Het toont de waarde voor . Ondersteunt gegevens die een verticale lijn vormen met uitzondering van alle 0 data.
|
|
6:RecipReg a/x+b
|
Past de modelvergelijking y=a/x+b toe op de gegevens door het gebruik van de kleinste-kwadraten methode op gelineariseerde data voor tenminste twee datapunten. Het toont waarden voor en ; en ook voor 2 en .
|
|
7:QuadraticReg
|
De QuadReg (kwadratische regressie) past de tweedegraads polynoom y=ax2+bx+c op de gegevens. Het toont waarden voor , en ; het toont ook de waarde voor 2. Voor drie datapunten is de vergelijking een veelterm fit (passend); voor vier of meer is het een veeltermregressie. Er zijn minimaal drie punten nodig.
|
|
8:CubicReg
|
Past de derdegraads polynoom y=ax3+bx2+cx+d toe op de gegevens. Het toont waarden voor , , en ; het toont ook een waarde voor 2. Voor vier punten is de vergelijking een veelterm fit (passend); voor vijf of meer is het een veeltermregressie. Er zijn minimaal vier punten nodig.
|
|
9:LnReg a+blnx
|
De logaritmische regressie past de modelvergelijking y=a+b ln(x) op de gegevens met behulp van de kleinste-kwadraten-methode en getransformeerde waarden ln(x) en y Het toont waarden voor en ; en ook voor 2 en .
|
|
:PwrReg ax^b
|
Past de modelvergelijkingy=axb op de gegevens met behulp van de kleinste-kwadraten-methode en getransformeerde waarden ln(x) en ln(y). Het toont waarden voor en ; en ook voor 2 en .
|
|
:ExpReg ab^x
|
De Exponentiële regressie past de modelvergelijking y=abx op de gegevens met behulp van de kleinste-kwadraten-methode en getransformeerde waarden x en ln(y). Het toont waarden voor en ; en ook voor 2 en .
|
|
: expReg ae^(bx)
|
Past de modelvergelijking y=a e^(bx) op de gegevens met behulp van de kleinste-kwadraten-methode op gelineariseerde data voor tenminste twee datapunten. Het toont waarden voor en ; en ook voor 2 en .
|
% u " toont het menu, dat de volgende verdelingsfuncties bevat:
|
1:Normalpdf
|
Berekent de kansdichtheidsfunctie (pdf) voor de normale verdeling bij een gespecificeerde x-waarde De standaardwaarden zijn gemiddelde mu=0 en standaard deviatie sigma=1. De kansdichtheidsfunctie (pdf) is:
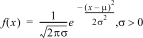
|
|
2:Normalcdf
|
Berekent de cumulatieve kans voor de normale kansverdeling tussen LOWERbnd (ondergrens) en UPPERbnd (bovengrens) voor het aangegeven gemiddelde mu en de standaarddeviatie sigma. De standaardwaarden zijn mu=0; sigma=1; met LOWERbnd = M1E99 en UPPERbnd = 1E99.
Opmerking: M1E99 tot 1E99 staat voor Moneindig tot oneindig.
|
|
3:invNormal
|
Berekent de inverse cumulatieve normale verdelingsfunctie voor een gegeven oppervlakte onder de normale verdelingskromme die bepaald wordt door gemiddelde mu en standaard deviatie sigma. Het berekent de x-waarde die overeenkomt met een oppervlakte aan de linkerkant van de x-waarde. 0 { oppervlakte { 1 moet waar zijn. De standaardwaarden zijn oppervlakte=1, mu=0 en sigma=1.
|
|
4:Binomialpdf
|
Berekent de kans op x voor de discrete binomiale verdeling met het gespecificeerde aantal pogingen en de succeskans (p) bij elke poging. x is een niet-negatief geheel getal dat kan worden ingevoerd met de opties SINGLE, LIST of ALL (een lijst van kansen van 0 tot aantal pogingen wordt teruggegeven). 0 { p { 1 moet waar zijn. De kansdichtheidsfunctie () is:
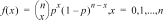
|
|
5:Binomialcdf
|
Berekent de cumulatieve kans op x voor de discrete binomiale verdeling met het gespecificeerde aantal pogingen en de succeskans (p) bij elke poging. x is een niet-negatief geheel getal dat kan worden ingevoerd met de opties SINGLE, LIST of ALL (lijst van cumulatieve kansen wordt teruggegeven). 0 { p { 1 moet waar zijn.
|
|
6:Poissonpdf
|
Berekent de kans op x voor de discrete Poisson-verdeling met het gespecificeerde gemiddelde mu (m), wat een reëel getal > 0 moet zijn. x kan een niet-negatief geheel getal zijn (SINGLE) of een lijst van integers (LIST). De standaardwaarde mu=1. De kansdichtheidsfunctie () is:
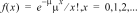
|
|
7:Poissoncdf
|
Berekent de cumulatieve kans op x voor de discrete Poisson-verdeling met het gespecificeerde gemiddelde mu, wat een reëel getal > 0 moet zijn. x kan een niet-negatief geheel getal zijn (SINGLE) of een lijst van integers (LIST). De standaardwaarde mu=1.
|
Statistiekresultaten
|
|
1-Var
|
Aantal x of (x,y) datapunten.
|
|
v
|
Beide
|
Gemiddelde van alle x waarden.
|
|
w
|
2-Var
|
Gemiddelde van alle y waarden.
|
|
|
Beide
|
Steekproef-standaarddeviatie van x.
|
|
|
2-Var
|
Steekproef-standaarddeviatie van y.
|
|
s
|
Beide
|
Populatie-standaarddeviatie van x.
|
|
s
|
2-Var
|
Populatie-standaarddeviatie van y.
|
|
G of G2
|
Beide
|
Som van alle x of x2 waarden.
|
|
G of G2
|
2-Var
|
Som van alle y of y2 waarden.
|
|
G
|
2-Var
|
Som van (xQy) voor alle xy paren.
|
|
|
2-Var
|
Helling van de lineaire regressie
|
|
|
2-Var
|
Snijpunt met de y-as van de lineaire regressie.
|
|
2 of
|
2-Var
|
Correlatiecoëfficiënt
|
|
¢
|
2-Var
|
Gebruikt a en b om de voorspelde x waarde te berekenen als er een y waarde wordt ingevoerd.
|
|
¢
|
2-Var
|
Gebruikt a en b om de voorspelde y waarde te berekenen als er een x waarde wordt ingevoerd.
|
|
of
|
Beide
|
Minimum of maximum van de x-waarden.
|
|
|
1-Var
|
Mediaan van de elementen tussen MinX en Med (1ste kwartiel)
|
|
|
1-Var
|
Mediaan van alle gegevens
|
|
|
1-Var
|
Mediaan van de elementen tussen Med en MaxX (3de kwartiel)
|
|
of
|
2-Var
|
Minimum of maximum van de y-waarden.
|
Het definiëren van statistische gegevens gaat als volgt:
|
1.
|
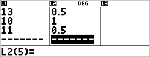
Voer gegevens in voor L1, L2 of L3 (Zie paragraaf Data Editor.) |
Opmerking: Niet-gehele frequentie-elementen zijn geldig. Dit is nuttig als frequenties worden ingevoerd als percentages of als delen die opgeteld 1 zijn. De steekproef-standaarddeviatie, Sx, is echter ongedefinieerd voor niet-gehele frequenties en Sx=Error wordt getoond voor die waarde. Alle andere statistische grootheden (maten) worden getoond.
|
2.
|
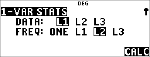
Druk op % u. Selecteer of en druk op <. |
|
3.
|
Selecteer L1, L2 of L3 en de frequentie |
|
4.
|
Druk op < om het menu met variabelen weer te geven. |
|
5.
|
Om gegevens te wissen drukt u op v v, selecteert u een lijst om te wissen en drukt u op <. |
Voorbeeld met 1-Var
Bereken het gemiddelde van {45,55,55,55}.
|
Alle gegevens wissen
|
v v $ $ $
|
|
|
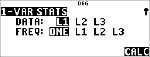
Data
|
<
$ $ $
<
|

|
|
Stat
|
% s
% u
|

|
|
|
(Selecteert )
$ $
|
|
|
|
<
|

|
|
Stat Var
|
<
|

|
|
|
V <
|

|
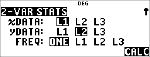
Voorbeeld met 2-Var
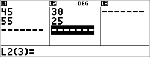
Data: (45,30); (55,25). Bereken: x¢(45).
|
Alle gegevens wissen
|
v v $ $ $
|

|
|
Data
|
< $ $ " $ $
|
|
|
Stat
|
% u
|

|
|
|
(Selecteert)
$ $ $
|
|
|
StatVars
|
< % s
% u
# # # # # #
|
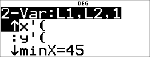
|
|
|
< ) <
|
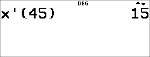
|
³ Opgave
Voor zijn laatste vier toetsen haalde Anthony de volgende scores. De toetsen 2 en 4 kregen een wegingsfactor van 0.5, en de toetsen 1 en 3 kregen een wegingsfactor van 1.
|
Toets Nr.
|
1
|
2
|
3
|
4
|
|
Score
|
12
|
13
|
10
|
11
|
|
Weging
|
1
|
0.5
|
1
|
0.5
|
|
1.
|
Bereken de gemiddelde score van Anthony (gewogen gemiddelde). |
|
2.
|
Waar staat de door de rekenmachine gegeven waarde n voor? Waar staat de door de rekenmachine gegeven waarde Gx voor? |
Onthoud: Het gewogen gemiddelde is
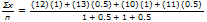
|
3.
|
De docent gaf Anthony 4 punten meer voor toets 4 vanwege een nakijkfout. Bereken de nieuwe gemiddelde score van Anthony. |
|
v v $ $ $
|

|
|
<
v " $ $ $ $
|
|
|
<
$ $ $ $
" $ $ $
<
|
|
|
% u
|

|
|
$ " " <
|
|
|
<
|
|
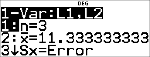
Anthony heeft een gemiddelde (v) van 11.33 (afgerond op honderdsten).
Op de rekenmachine staat n voor de totale som van de wegingsfactoren.
n = 1 + 0.5 + 1 + 0.5.
Gx staat voor de gewogen som van zijn scores.
(12)x(1) + (13)x(0.5) + (10)x(1) + (11)x(0.5) = 34.
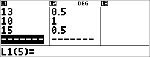
Verander Anthony's laatste score van 11 in 15.
|
v $ $ $ <
|
|
|
% u
$ " " < <
|

|
Als de docent 4 punten meer geeft voor toets 4, is 12 de gemiddelde score van Anthony.
³ Opgave
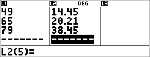
De onderstaande tabel geeft de resultaten van een remtest.
|
Toets Nr.
|
1
|
2
|
3
|
4
|
|
Snelheid (km/u)
|
33
|
49
|
65
|
79
|
|
Remafstand (m)
|
5.30
|
14.45
|
20.21
|
38.45
|
Gebruik het verband tussen snelheid en remafstand om de remafstand te schatten die nodig is bij een voertuig dat 55 km/u rijdt.
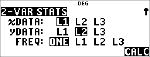
Een met de hand getekende scatterplot van deze gegevens suggereert een lineair verband. De rekenmachine gebruikt de kleinste-kwadraten-methode om de best passende lijny'=ax'+bte berekenen bij de gegevens die ingevoerd zijn in lijsten.
|
v v $ $ $
|

|
|
<
$ $ $ $ " $ $ $ <
|
|
|
% s
% u
|

|
|
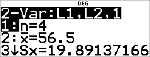
(Selecteert )
$ $ $
|
|
|
<
|
|
|
Druk op $ om a en b te bekijken.
|
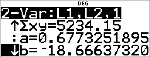
|
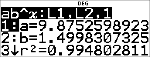
Deze best passende lijn, y'=0.67732519x'N18.66637321 drukt de lineaire trend van de gegevens uit.
|
Druk op $ tot y' gemarkeerd is.
|

|
|
< ) <
|

|
Het lineaire model geeft een geschatte remafstand van 18.59 meter voor een voertuig dat 55 km/u rijdt.
Regressie voorbeeld 1
Bereken een ax+b lineaire regressie voor de volgende data: {1,2,3,4,5}; {5,8,11,14,17}.
|
Alle gegevens wissen
|
v v $ $ $
|

|
|
Data
|
<
$ $ $ $
$ "
$ $ $ $
<
|
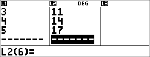
|
|
Regressie
|
% s
% u
$ $ $
|

|
|
|
<
|
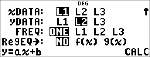
|
|
|
$ $ $ $
<
Druk op $ om alle resultaat-variabelen te onderzoeken.
|

|
Regressie voorbeeld 2
Bereken een exponentiële regressie voor de volgende data:
|
•
|
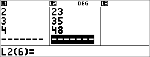
L1 = {0,1,2,3,4}; L2 = {10,14,23,35,48} |
|
•
|
Bepaal de gemiddelde waarde van de data in L2. |
|
•
|
Vergelijk de waarden van de exponentiële regressie met die in L2. |
|
Alle gegevens wissen
|
v v
|
|
|
Data
|
$ $ $ $
$ " $ $ $ $ <
|
|
|
Regressie
|
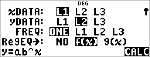
% u
# #
|
|
|
Sla de regressie-vergelijking op
in f(x) in het menu I.
|
< $ $ $ "
<
|
|
|
Regressievergelijking
|
<
|
|
|
Bepaal de gemiddelde waarde (y) van de data in L2 met behulp van StatVars.
|
% u
(Kiest )
$ $ $
$ $ $
$ $
|
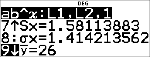
Merk op dat de bovenste regel u herinnert aan uw laatste statistische of regressie berekening.
|
|
Bestudeer de tabel met waarden van de regressie vergelijking.
|
I
|

|
|
|
< $
<
<
|

|
|
|
< <
|
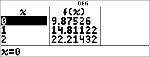
|
Waarschuwing: Als u nu 2-Var Stats berekent voor uw data, dan zullen de variabelen en (samen met en 2) worden berekend als een lineaire regressie. Bereken niet opnieuw 2-Var Stats na een andere regressieberekening als u uw regressie-coëfficiënten (a, b, c, d) en r-waarden voor uw specifieke opgave in het menu wilt bewaren.
Verdeling voorbeeld
Bereken de kans met de binomiale kansverdeling voor de x-waarden {3,6,9} met 20 pogingen en een succeskans van 0.6. Voer de x-waarden in lijst L1 in, sla de resultaten op in L2, en bepaal de som van de kansen en sla die op in de variabele t.
|
Alle gegevens wissen
|
v v $ $ $
|

|
|
Data
|
<
$ $
<
|
|
|
DISTR
|
% u "
$ $ $
|

|
|
|
< "
|
|
|
|
<
$
|
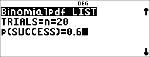
|
|
|
< $ $
|
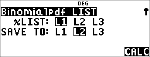
|
|
|
<
|
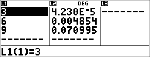
|
|
|
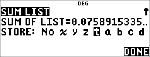
v ! "
<
|
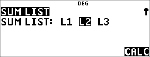
|
|
|
<
" " " "
< <
|
|