U bent hier: TI-30X Pro MathPrint™ Wetenschappelijke rekenmachine > Math Functies > Numerieke integraal

Numerieke integraal

De TI-30X Pro MathPrint™ berekent de (benaderde) numerieke integraal van een uitdrukking met betrekking tot een variabele x, bij een gegeven ondergrens, een bovengrens en een tolerantie voor de numeriek methode.

MathPrint™-modus

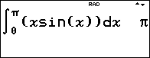
% Q plakt het template voor de numerieke integraal vanaf het toetsenbord om de numerieke integraal voor een bepaald interval te berekenen met de standaard tolerantie H is 1EM5.

Voorbeeld voor hoeken in de modus RADIAN (radialen)

% Q

q " <

% Q

0 " g " "

z X z ) "

<

Om de standaard tolerantie, H te veranderen en te bekijken hoe de tolerantie een rol speelt in de numerieke oplossing, kunt u de numerieke integraal plakken vanaf de menu locatie d MATH 8:fnInt(, waar het template voor de numerieke integraal wordt geplakt met de optie om de tolerantie te wijzigen voor een onderzoek naar het resultaat van de numerieke integraal.

Voorbeeld in de hoekmodus DEGREE (in graden)

d MATH 8:fnInt(

met optionele tolerantie

q <

d 8

0 " 3 "

z G 5 <

Classic Modus of Classic invoer

In Classic modus of in classic bewerkingsregels wordt de fnInt( opdracht geplakt vanaf het toetsenbord of het menu MATH.

Syntax: fnInt(uitdrukking,variabele,boven,onder[,tolerantie]) waar tolerantie optioneel is en de standaard H is ingesteld is op 1EM5.

Voorbeeld

% Q

or

d MATH 8:fnInt(

% Q

z G 5 % .

z % .0 % .3 )

<

³ Opgave

Bepaal de oppervlakte onder de kromme f(x) = Mx2+4 op de x-intervallen van M2 to 0 en daarna van 0 tot 2. Wat valt u op bij deze resultaten? Wat kunt u zeggen over de grafiek van deze functie?

% Q M 2 " 0 "

M z F T 4 " r

<

# # <

% ! " 0 J

" 2

<

Merk op dat beide oppervlaktes hetzelfde zijn. Omdat dit een parabool is met de top op (0,4) en met nulpunten bij (M2,0) en (2,0) ziet u dat de symmetrische oppervlakten gelijk zijn.