% A
% A
z F T 5 z " "
M 1 <
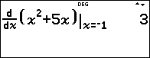
De TI-30X Pro MathPrint™ berekent (een benadering van) de numerieke afgeleide van een uitdrukking in een punt, met een tolerantie zoals die is vastgelegd voor deze numerieke methode. (Zie de paragraaf Over de numerieke afgeleide in een punt voor meer informatie.)
% A plakt het sjabloon voor de numerieke afgeleide van het toetsenbord om de numerieke afgeleide te berekenen met de standaard tolerantie H is 1EM5.
|
% A |
% A z F T 5 z " " M 1 < |
|
Om de standaard tolerantie, H te veranderen en te bekijken hoe de tolerantie een rol speelt in de numerieke oplossing, plakt u de numerieke afgeleide vanaf de menu-locatie, d MATH 7:nDeriv(, waar het sjabloon voor de numerieke afgeleide wordt geplakt met de optie om de tolerantie te wijzigen zoals nodig voor een onderzoek naar het resultaat van de numerieke afgeleide.
|
d MATH 7:nDeriv( met optionele tolerantie |
d 7 z F T 5 z " " M 1 " 1 E M 5 < |
|
In Classic modus of in classic bewerkingsregels wordt de opdracht nDeriv( geplakt vanaf het toetsenbord of vanuit het menu MATH.
Syntax: nDeriv(uitdrukking,variabele,punt[,tolerantie]) waar tolerantie optioneel is en de standaard H is ingesteld op 1EM5.
|
% A or d MATH 7:nDeriv( |
% A z F T 5 z % ` z % ` M 1 ) < |
|
De opdracht voor de numerieke afgeleide in een punt, nDeriv( of d/dx, gebruikt de symmetrische verschil-quotiënt methode. Deze methode benadert de numerieke afgeleide in een gegeven punt als de helling van de koorde in de buurt van dat punt.
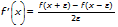
Als H kleiner wordt, zal de benadering voor de helling van de raaklijn in het gegeven punt x gewoonlijk nauwkeuriger worden.
| • | Vanwege de gebruikte methode voor het berekenen van de numerieke afgeleide in een punt kan de rekenmachine een foutieve waarde voor de afgeleide geven in een niet-differentieerbaar punt. |
| • | Zorg dat u altijd enige kennis heeft over het gedrag van de functie in de buurt van het punt door gebruik van een tabel met waardes in de buurt van dat punt (of een grafiek van de functie). |
Bepaal de helling van de raaklijn van de functie f(x) = x2 - 4x voor x = 2. Wat merk je op?
|
% A z F U 4 z " " 2 < |
|