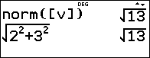Définissez [u]
% [

< " <

<
1 P 2 < 8 <

Définissez [v]
% [
" <

<
2 < 3 <

Ajoutez des vecteurs
% s
% [
T
% [

<
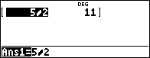
DotP
- -
% [

% [
% `
% [

) <
.5 V 2 T 8 V 3 <
Remarque : DotP est calculé ici de deux façons.

norm
-
% [
% [
<

% b 2 F T 3 F "
<
Remarque : norm est calculée ici de deux façons.