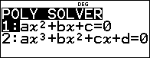Vous êtes ici: Guide de la calculatrice scientifique TI-30X Pro MathPrint™ > Outils mathématiques > Solveurs

Solveurs

Solveur d'équations numériques

% ‰

% ‰ vous invite à spécifier l'équation et les valeurs des variables. Vous sélectionnez ensuite l'inconnue.

Exemple

Pour l'équation suivante, résoudre par rapport à la variable b.

Rappel : Si vous avez déjà affecté des valeurs à des variables, le solveur en tient compte.

Num-solv

% ‰

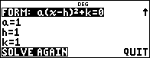
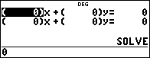
Partie gauche

1 P 2 " z F

U 5 z z z

z z " "

Partie droite

6 z U z z

z z z z

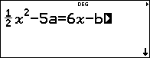
Valeur initiale de la variable

<

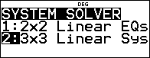
1 P 2 "

 

<

2 P 3 "

 

<

1 P 4 "

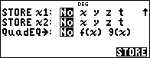
Sélectionnez la variable de résolution

< " "

Bornes de la solution

< $ $

Saisissez l'intervalle dans lequel vous cherchez la solution sous la forme [BORNE INFÉRIEURE,BORNE SUPÉRIEURE], si nécessaire.

 

<

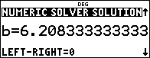
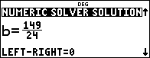
r

Remarque : LEFT-RIGHT correspond à la différence entre la partie gauche et la partie droite de l'équation évaluées au point solution. Cette différence indique le degré de proximité de la solution par rapport à la réponse exacte.

Solveur de polynômes

% Š

% Š vous invite à sélectionner le solveur d'équation du second ou du troisième degré. Saisissez ensuite les coefficients réels des variables et résolvez l'équation. Les solutions sont réelles ou complexes.

Exemple d'équation du second degré

Rappel : Si vous avez déjà affecté des valeurs à des variables, le solveur en tient compte.

Poly-solv

% Š

Saisissez les coefficients

<

1

 

$

M 2

 

$

2

<

Solutions

<

 

$

 

$

Remarque : Si vous choisissez de stocker le polynôme dans
f(x) ou g(x), vous pouvez utiliser I pour étudier le tableau de valeurs.

 

$ $ $ <

Forme canonique (solveur du second degré uniquement)

Sur les écrans de solution du solveur de polynômes, vous pouvez appuyer sur r pour basculer entre le format du nombre de solutions x1, x2 pour le second degré et x1, x2, x3 pour le troisième degré.

Solveur de système d'équations linéaires

% ‹

% ‹ permet de résoudre des systèmes d'équations linéaires. Vous avez le choix entre les systèmes 2×2 ou 3×3.

Remarques :

• Les résultats x, y et z sont automatiquement stockés dans les variables x, y et z.
• Utilisez r pour alterner entre les types de résultats (x, y et z), si nécessaire.
• Le solveur de système calcule une solution unique ou des solutions infinies sous une forme fermée, ou il indique l'absence de solution.

Exemple de système 2×2

Résolvez :

 

Sys-solv

% ‹

Système 2×2

<

Saisissez les équations

1 P 3 < <

2 P 3 <

37 P 90 <

2 P 5 <

U 1 P 5 <

28 P 75 <

Solution

<

Changez de format de nombre (si nécessaire)

r

 

<

Changez de format de nombre (si nécessaire)

r

 

<

Exemple de système 3×3

Résolvez :

5x – 2y + 3z = -9

4x + 3y + 5z = 4

2x + 4y – 2z = 14

 

Sys-solv

% ‹ $

Système 3×3

<

Saisissez les coefficients

5 < M 2 < 3 < M 9 <

4 < 3 < 5 < 4 <

2 < 4 < M 2 < 14 <

Remarque : Pour 3x3, notez que la première équation doit être saisie de la façon suivante :

5x + M2 + 3z = M9

Solution

<

 

<

 

<

 

<

Remarque : Appuyez sur r pour changer de format de nombre si nécessaire.

Exemple de système 3×3 avec une infinité de solutions

Entrez les éléments du système

% ‹ 2

1 < 2 < 3 < 4

<

2 < 4 < 6 < 8

<

3 < 6 < 9 < 12

<

Solution

<

 

<

 

<

 

<

 

<