Définissez la matrice [A] =
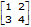
En plus de celles disponibles dans le menu Matrix MATH, les opérations matricielles suivantes sont acceptées. Les dimensions doivent être correctes :
| • | matrice + matrice |
| • | matrice – matrice |
| • | matrice × matrice |
| • | Multiplication par un scalaire (par exemple, 2 × matrice) |
| • | matrice × vecteur (vecteur sera interprété comme un vecteur de colonne) |
% t NAMES
% t affiche le menu NAMES associé, qui présente les dimensions des matrices et permet de les utiliser dans des calculs. Le nombre de lignes et de colonnes d'une matrice peuvent être : 1{ligne{3 et 1{colonne{3.
|
1 : [A] |
Matrice [A] définissable. |
|
2 : [B] |
Matrice [B] définissable. |
|
3 : [C] |
Matrice [C] définissable. |
|
4 : [Ans] |
Dernier résultat matriciel ([Ans]=ligne×colonne) ou dernier résultat vectoriel ([Ans] dim=n). Non modifiable. Remarque : Vous pouvez basculer entre les formats des valeurs dans les cellules. Pour afficher le format exact ou un niveau de précision complet, mettez la cellule en surbrillance. |
|
5 : [I2] |
Matrice unité 2×2 (non modifiable). |
|
6 : [I3] |
Matrice identité 3×3 (non modifiable). |
% t MATH
% t " affiche le menu MATH associé, qui permet d'effectuer les opérations suivantes :
|
1 : Determinant |
Déterminant d'une matrice carrée. Syntaxe : det(matrice carrée) |
|
2 : T Transpose |
Transposée d'une matrice. Syntaxe : matriceT |
|
3 : Inverse |
Inverse d'une matrice carrée. Syntaxe : matrice carrée–1 |
|
4 : ref reduced |
Forme échelonnée (réduite de Gauss). Syntaxe : Gauss(matrice) |
|
5 : rref reduced |
Forme échelonnée réduite (réduite de Gauss-Jordan). Syntaxe : Gauss-Jordan(matrice) |
% t EDIT
% t ! affiche le menu EDIT associé, qui permet de définir ou de modifier la matrice [A], [B] ou [C].
Remarque : Appuyez sur r pour basculer au besoin entre les différents formats de nombre dans une cellule.
|
Définissez la matrice [A] = |
|
Calculez le déterminant, la transposée, l'inverse et la réduite de Gauss-Jordan de la matrice [A].
|
Définissez [A] |
% t ! |
|
|
|
< |
|
|
Définissez les dimensions |
" < " < < |
|
|
Entrez les valeurs |
1 $ 2 $ 3 $ 4 $ |
|
|
det([A]) |
% s % t " |
|
|
|
< % t < ) < |
|
|
Transposée |
% t < % t " $ < |
|
|
|
< |
|
|
Inverse |
% s - % t < % t " $ $ < |
|
|
|
< |
|
|
Réduite de Gauss-Jordan |
- - % t " # |
|
|
|
< % t < ) |
|
|
|
< |
|