% Q
q " <
% Q
0 " g " "
z X z ) "
<
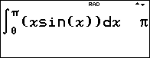
% Q colle le modèle d'intégrale numérique à partir du clavier afin de calculer l'intégrale numérique sur un intervalle donné, avec la tolérance par défaut H égale à 1EM5.
|
% Q |
q " < % Q 0 " g " " z X z ) " < |
|
Pour modifier la tolérance par défaut, H, et observer le rôle qu'elle joue dans la solution numérique, collez l'intégrale numérique à partir de l'emplacement du menu, d MATH 8:fnInt(, où le modèle d'intégrale numérique sera collé avec la possibilité de modifier la tolérance si nécessaire aux fins d'étudier le résultat obtenu.
|
d MATH 8:fnInt( avec la tolérance facultative |
q < d 8 0 " 3 " z G 5 < |
|
En mode Classic ou dans les lignes de saisie Classic, la commande fnInt( colle les entrées à partir du clavier ou du menu MATH.
Syntaxe : fnInt(expression,variable,borne supérieure,borne inférieure[,tolérance]) où tolérance est facultatif et la valeur par défaut de H est 1EM5.
|
% Q ou d MATH 8:fnInt( |
% Q z G 5 % . z % .0 % .3 ) < |
|
Calculez l'aire sous la courbe f(x) = Mx2+4 sur les intervalles x, de M2 à 0, puis de 0 à 2. Que remarquez-vous concernant les résultats ? Que pourriez-vous dire de la courbe représentative de cette fonction ?
|
% Q M 2 " 0 " M z F T 4 " r |
|
|
< |
|
|
# # < % ! " 0 J " 2 |
|
|
< |
|
Notez que les deux aires sont égales. Comme il s'agit d'une parabole avec le sommet en (0,4) et des zéros en (M2,0) et (2,0), vous observez que les aires symétriques sont égales.