% A
% A
z F T 5 z " "
M 1 <
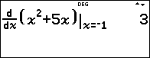
La TI-30X Pro MathPrint™ calcule une valeur approchée de la dérivée numérique d'une expression en un point avec une tolérance donnée pour la méthode numérique. (Pour plus d'informations, voir la section À propos de la dérivée numérique en un point.)
% A colle le modèle de dérivée numérique à partir du clavier afin de calculer la dérivée numérique selon la tolérance par défaut H égale à 1EM5.
|
% A |
% A z F T 5 z " " M 1 < |
|
Pour modifier la tolérance par défaut, H, et observer le rôle qu'elle joue dans la solution numérique, collez la dérivée numérique à partir de l'emplacement du menu, d MATH 7:nDeriv(, où le modèle de dérivée numérique sera collé avec la possibilité de modifier la tolérance si nécessaire aux fins d'étudier le résultat obtenu.
|
d MATH 7:nDeriv( avec la tolérance facultative |
d 7 z F T 5 z " " M 1 " 1 E M 5 < |
|
En mode Classic ou dans les lignes de saisie Classic, la commande nDeriv( colle les entrées à partir du clavier ou du menu MATH.
Syntaxe : nDeriv(expression,variable,point[,tolérance]) où tolérance est facultatif et la valeur par défaut de H est 1EM5.
|
% A ou d MATH 7:nDeriv( |
% A z F T 5 z % ` z % ` M 1 ) < |
|
La commande de dérivée numérique en un point, nDeriv( ou d/dx, fait appel à la méthode du quotient des différences symétriques. Cette méthode calcule la valeur approchée de la dérivée numérique en un point donné comme la pente de la droite sécante par rapport à ce point.
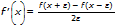
À mesure que H diminue, l'approximation devient généralement plus précise pour calculer la valeur approchée de la pente de la tangente au point donné x.
| • | En raison de la méthode appliquée pour calculer la dérivée numérique en un point, la calculatrice peut renvoyer une valeur fausse pour la dérivée en un point où la fonction n'est pas dérivable. |
| • | Ayez toujours des notions concernant le comportement de la fonction située au voisinage du point en utilisant une table de valeurs près du point (ou une représentation graphique de la fonction). |
Déterminez la pente de la tangente à la fonction f(x) = x2 - 4x en x = 2. Que remarquez-vous ?
|
% A z F U 4 z " " 2 < |
|