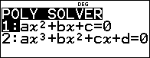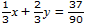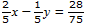You are here: TI-30X Pro MathPrint™ Scientific Calculator > Math Tools > Solvers

Solvers

Numeric Equation Solver

% ‰

% ‰ prompts you for the equation and the values of the variables. You then select the variable you want to solve.

Example

For the following equation shown, solve for the variable b.

Reminder: If you have already defined variables, the solver will assume those values.

Num-solv

% ‰

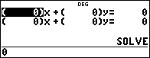
Left side

1 P 2 " z F

U 5 z z z

z z " "

Right side

6 z U z z

z z z z

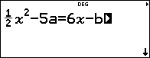
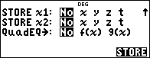
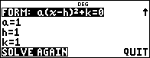
Initial Variable Value

<

1 P 2 "

 

<

2 P 3 "

 

<

1 P 4 "

Select Solution Variable

< " "

Solution Bounds

< $ $

Enter the interval where you expect the solution as [LOWER,UPPER] if needed.

 

<

r

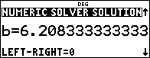
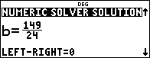
Note: LEFT-RIGHT is the difference between the left- and right-hand sides of the equation evaluated at the solution. This difference gives how close the solution is to the exact answer.

Polynomial Solver

% Š

% Š prompts you to select either the quadratic or the cubic equation solver. You then enter the real coefficients of the variables and solve. Solutions will be real or complex.

Example of Quadratic Equation

Reminder: If you have already defined variables, the solver will assume those values.

Poly-solv

% Š

Enter coefficients

<

1

 

$

M 2

 

$

2

<

Solutions

<

 

$

 

$

Note: If you choose to store the polynomial to
f(x) or g(x), you can use I to study the table of values.

 

$ $ $ <

Vertex form (quadratic solver only)

On the solution screens of the polynomial solver, you can press r to toggle the number format of the solutions x1, x2 for quadratic, or x1, x2, and x3 for cubic.

System of Linear Equations Solver

% ‹

% ‹ solves systems of linear equations. You choose from 2×2 or 3×3 systems.

Notes:

• x, y, and z results are automatically stored in the x, y, and z variables.
• Use r to toggle the results (x, y and z) as needed.
• The system solver solves for a unique solution or infinite solutions in closed form, or it indicates no solution.

Example 2×2 System

Solve:

 

Sys-solv

% ‹

2×2 system

<

Enter equations

1 P 3 < <

2 P 3 <

37 P 90 <

2 P 5 <

U 1 P 5 <

28 P 75 <

Solution

<

Change number format (if needed)

r

 

<

Change number format (if needed)

r

 

<

Example 3×3 System

Solve:

5x – 2y + 3z = -9

4x + 3y + 5z = 4

2x + 4y – 2z = 14

 

Sys-solv

% ‹ $

3×3 system

<

Enter coefficients

5 < M 2 < 3 < M 9 <

4 < 3 < 5 < 4 <

2 < 4 < M 2 < 14 <

Note: For 3x3, notice that the first equation must be entered as:

5x + M2 + 3z = M9

Solution

<

 

<

 

<

 

<

Note: Press r to change the number format if needed.

Example 3×3 System with Infinite Solution

Enter the system

% ‹ 2

1 < 2 < 3 < 4

<

2 < 4 < 6 < 8

<

3 < 6 < 9 < 12

<

Solution

<

 

<

 

<

 

<

 

<